Отчет по практике для ПГС. Метрология наука, которая направлена на облегчение единства измерений, изучает приборы и методы измерений, проводит испытание. Физическая величина
 Скачать 3.81 Mb. Скачать 3.81 Mb.
|
ВОПРОС 4:Основы теории измерения Погрешность – отклонение результата измерения от истинного (действительного) Относительная погрешность – отношение абсолютной погрешности к модулю приближённого значения (к истинному значению). Абсолютная погрешность – модуль разности между истинным значением величины и её приближённым значением. (отклонение результата анализа от истинного (или среднего) значения). Точность – близость измерения к истинному значению. Промах – результат стремится максимально отклониться от истинного. Метод измерений – совокупность приёмов использования принципов и средств измерений. Мера – средство измерения, которое воспроизводит ФВ. Систематической погрешностьюизмерения называется составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Причиной появления систематических погрешностей могут быть неисправности измерительной аппаратуры, несовершенство метода измерения, неправильная установка измерительных приборов и отступление от нормальных условий их работы, особенности и неправильные действия самого оператора. Случайной погрешностьюизмерения называется составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же физической величины. Наличие случайных погрешностей выявляется при проведении ряда измерений этой величины, когда оказывается, что результаты измерений не совпадают друг с другом. Обычно случайные погрешности возникают из-за одновременного действия многих случайных причин, каждая из которых в отдельности мало влияет на результат измерения. Поэтому нет простых способов избавиться от случайных погрешностей. Целью обработки результатов измерений в метрологии является получение наиболее достоверных значений измеряемых величин и оценка погрешностей измерений. Среднеквадратическое отклонение значений множества заданных чисел от среднего арифметического определяется как число равное квадратному корню от суммы квадратов разности этих чисел и среднего арифметического, делённой на количество этих чисел 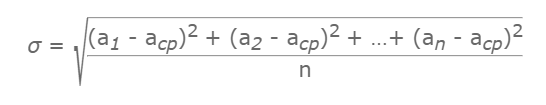 Правила округления результатов расчёта: 1. Точность результатов измерений и точность вычислений при обработке результатов измерений должны быть согласованы с требуемой точностью получаемой оценки измеряемой величины. Пояснение: число знаков после запятой в оценке измеряемой величины должно совпадать с числом знаков после запятой в значении погрешности, погрешность выражается в абсолютных величинах. 2 Погрешность оценки измеряемой величины следует выражать не более чем двумя значащими цифрами. Две значащие цифры в погрешности оценки измеряемой величины сохраняют: - при точных измерениях; - если первая значащая цифра не более трех. Пояснение: данный пункт описывает с какой точностью следует выражать погрешность измерения. Вычисленная погрешность обладает собственной погрешностью, как правило выше 10-20 процентов, следовательно, нет необходимости описывать её более чем двумя знаками. Например, числа - 0,610 и 0,616 отличаются друг от друга не более чем на 1%. Причём, чем первая значащая цифра больше, тем результат округления внесёт меньшую погрешность, поэтому, если первая значащая цифра в погрешности больше 3, погрешность округляют до одной значащей цифры. 3 Число цифр в промежуточных вычислениях при обработке результатов измерений должно быть на две больше, чем в окончательном результате. 4 Погрешность при промежуточных вычислениях должна быть выражена не более чем тремя значащими цифрами. Пояснение: эти два правила применяются только для ручных вычислений, для уменьшения трудоёмкости. При подсчёте с помощью ЭВМ и т.п. промежуточные результаты без необходимости не округляют. 5 Сохраняемую значащую цифру в погрешности оценки измеряемой величины при округлении увеличивают на единицу, если отбрасываемая цифра не указываемого младшего разряда больше либо равна пяти, и не изменяют, если она меньше пяти. Пояснение: Это стандартное правило округления. |
