Микроэлектроника
 Скачать 3.37 Mb.
|
Таблица 3.2
Пример 3.2. Перевести десятичное число 15710 в восьмеричный код, результат проверить.
Проверка: 2358 = 282 + 381 + 580 = 128 + 24 + 5 = 15710. Пример 3.3. Перевести десятичное число 15710 в шестнадцатеричный код, результат проверить.
Проверка: 9D16 = 9161 + 13160 = 144 + 13 = 15710. С помощью байта данных можно представить различную информацию: – целое число без знака (от 0 до 255); – число от 0 до 99 в двоично-десятичном коде; – машинный код команд микропроцессора; – состояние восьми датчиков; – двоичное число со знаком в прямом, обратном или дополнительном коде Х, где Х – модуль числа (от 0 до 127), для отображения которого используется семь младших разрядов. Старший разряд – знаковый (0 – для положительных чисел, 1 – для отрицательных). Пример: +16 -16 прямой код 0, Х 000100001, Х 10010000 обратный код 0, Х 000100001,  11101111дополнительный код0, Х 000100001,  11110000Прямой, обратный и дополнительный коды положительных чисел совпадают. Для получения дополнительного кода отрицательного числа можно проинвертировать код положительного числа и прибавить единицу. Дополнительный код однобайтового числа минус Х равен дополнению до 256, т.е. двоичному коду числа  . Преобразование дополнительного кода числа в прямой осуществляется по тому же правилу, что прямого в дополнительный.Пример 3.4. Записать дополнительный код однобайтового числа минус 100. Для отображения знака используется старший разряд числа. Решение. Запишем двоичный код числа плюс 100: 01100100 Проинвертируем его: 10011011 Прибавим единицу: 10011100 Проверка. 10011100=128+16+8+4=156=256-100. Ответ: дополнительный код числа минус 100 равен 10011100В.
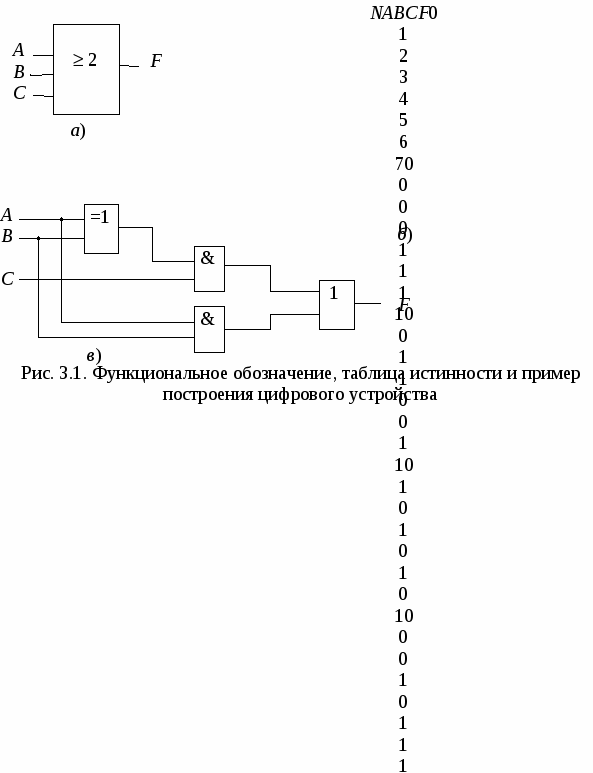 На рис. 3.1, а приведено функциональное обозначение цифрового устройства с тремя входами и одним выходом. Каждый из входных сигналов А, В и С может принимать лишь два значения: 1 и 0. Выходной сигнал F, который можно рассматривать как логическую функцию входных переменных А, В, С, на каждом их наборе F может быть равен 1 или 0. В простейшем случае функция F(A,B,C) может быть задана словесным описанием. Например, функция F равна 1, если все три ее переменные или любая пара из них равны 1, в противном случае F = 0. Любая логическая функция может быть задана в виде таблицы истинности. На рис. 3.1, б представлена таблица истинности для функции трех переменных, описанной выше словесно. Она определена на восьми наборах, которые располагаются в порядке нарастания десятичного эквивалента Nих двоичного кода. В правом столбце указаны значения логической функции Fна каждом наборе. Задание логической функции таблицей истинности не всегда удобно, так как при большом числе переменных она становится слишком громоздкой. В этом смысле наиболее привлекателен аналитический способ задания функций в виде так называемых структурных формул, показывающих, какие логические операции необходимо выполнить над входящими в них переменными, чтобы получить значения данной функции. 3.3. Совершенная дизъюнктивная нормальная форма По таблице истинности можно составить выражение для логической функции в СДНФ (совершенной дизъюнктивной нормальной форме), т.е. в виде суммы логических произведений, соответствующих единичным наборам функции:  (3.2)Выражение (3.2) записано с использованием операций логического сложения (дизъюнкции), логического умножения (конъюнкции) и логического отрицания (инверсии), которые выполняют простейшие логические элементы ИЛИ, И и НЕ соответственно. Для каждого единичного набора составляется логическое произведение входных переменных, в которое переменная входит с инверсией при нулевом ее значении на данном наборе. Эти логические произведения объединяются затем знаком логического сложения (+ или ). На рис. 3.2 представлены таблицы истинности и условные графические обозначения двухвходовых логических элементов. Кроме указанных выше, на практике широко используются элементы И-НЕ, ИЛИ-НЕ, Исключающее ИЛИ. Логическая функция последнего (функция «неравнозначность» или сумма по модулю два) в СДНФ записывается в виде  Логические функции, представляющие собой дизъюнкции отдельных членов, каждый из которых есть некоторая функция, содержащая только конъюнкции, называют логическими функциямидизъюнктивной нормальной формы (ДНФ), например:  . Если же каждый член дизъюнкции нормальной формы от n аргументов содержит все эти аргументы, часть которых входит в него с инверсией, а часть – без нее, то такая форма представления функции называется совершенной дизъюнктивной нормальной формой(СДНФ), например: К  аждая конъюнкция этой дизъюнкции включает каждую переменную только один раз в прямом или инверсном виде, обращаясь в единицу при определенном наборе значений переменных, и носит название минтерм. Правило перехода от табличного задания логической функции к ее записи в СДНФ (правило записи логической функции по единицам) заключается в следующем: 1. Составить минтермы для строк таблицы истинности, на которых функция F равна 1. Если значение переменной в этой строке равно 0, то в минтерме записывается отрицание этой переменной. 2. Записать дизъюнкцию составленных минтермов, которая будет представлять переключательную функцию в СДНФ. 3.4. Основные законы булевой алгебры Математический аппарат, описывающий действия цифровых устройств, базируется на алгебре логики, автором которой считается английский математик Дж. Буль (1815 – 1864 г.). В практических целях первым применил его американский ученый К. Шеннон в 1938 г. при исследовании электрических цепей с контактными выключателями. В алгебре логики имеется четыре основных закона: 1. Переместительный, или закон коммутативности для операций сложения и умножения соответственно: A+B = B+A; AB = BA. 2. Сочетательный, или закон ассоциативности для сложения и умножения соответственно: (A + B)+C = A+(B + C); (AB)C = A(BC). 3. Распределительный, или закон дистрибутивности для сложения и умножения соответственно: (A+B)C = AC + BC; (AB)+C = (A + C) (B + C). 4. Закон двойственности или инверсии (правило де Моргана) сложения и умножения соответственно:  Справедливость этих законов можно доказать с помощью таблиц истинности сложных логических связей, описываемых законом, или с помощью логических преобразований. Для преобразований логических выражений пользуются легко доказываемыми тождествами, вытекающими из принципа работы простейших логических элементов (аксиомы алгебры Буля): Х+1=1; Х·1=Х;  ;X+0= Х; X·0=0 ; X 0 =Х; X+X=Х; X·X=Х; X X=0;  ;  ;  .С помощью законов алгебры логики и тождеств могут быть доказаны соотношения, получившие названия правил: поглощения A +AB = A, A(A +B) = A и склеивания  Эти правила широко используют для преобразования переключательных функций с целью их упрощения. Из правила де Моргана вытекают следствия:  с помощью которых появляется возможность выражать дизъюнкцию через конъюнкцию и отрицание, а конъюнкцию – через дизъюнкцию и отрицание. Законы двойственности справедливы для любого числа переменных. В булевой алгебре при отсутствии в выражении скобок вводится следующий порядок действий: первыми выполняются операции отрицания, далее – конъюнкции, затем – дизъюнкции. Наличие в выражении скобок изменяет обычный порядок действий: в первую очередь должны выполняться операции внутри скобок. Записанная ранее в СДНФ логическая функция трех переменных (3.2) может быть представлена в виде (ей соответствует схема устройства на рис. 3.1, в):  .Набор логических элементов И, ИЛИ, НЕ называют основным базисом или основной функционально полной системой элементов. Последнее означает, что с помощью этих элементов можно реализовать устройство, осуществляющее сколь угодно сложную логическую операцию. Каждый из элементов И-НЕ и ИЛИ-НЕ также обладает функциональной полнотой. Базисы И-НЕ и ИЛИ-НЕ называют универсальными. Эти базисы приобрели важное значение в связи с широким использованием интегральных логических элементов при построении логических устройств. С 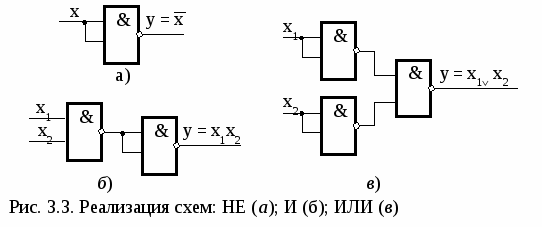 труктуры логических элементов НЕ, И, ИЛИ, построенных из элементов И-НЕ, приведены на рис. 3.3. Схема отрицания НЕ реализована на использовании следующего соотношения:  .Схема логического умножения использует принцип двойной инверсии:  .Схема логического сложения двух сигналов базируется на использовании закона отрицания:  .Связующим звеном между реальным элементом и его переключательной функцией служит полярность логики. Различают положительную и отрицательную логику. При положительной логике в качестве логической единицы принят высокий уровень сигнала, при отрицательной логике – низкий уровень сигнала. Из принципа дуальности следует, что одно и то же логическое выражение может быть представлено двояко, например, y = x 1 x 2 и  .Это значит, что один и тот же элемент будет реализовывать с точки зрения положительной логики функцию конъюнкции, а с точки зрения отрицательой логики – дизъюнкцию. В дальнейшем в качестве единицы будет принят высокий уровень напряжения (положительная логика). Минимизация– процесс приведения булевых функций к такому виду, который допускает наиболее простую, с наименьшим числом элементов, физическую реализацию функции. Частная задача минимизации булевой функции сводится к такому представлению заданной функции, которое содержит наименьшее возможное число букв и наименьшее возможное число операций над ними, так как каждой элементарной логической функции соответствует определенный физический элемент. Оценить различные представления одной и той же булевой функции, например ДНФ, можно по количеству входов логических элементов, реализующих заданную функцию. Для минимизации переключательных функций применяют различные методы: последовательного исключения переменных с помощью законов алгебры логики, с использованием диаграмм Венна, карт Карно (Вейча) и др.
Логические функции можно отобразить на диаграммах Венна. Пусть левый круг (рис. 3.5) соответствует области прямых значений переменной А, правый – области прямых значений переменной В. Тогда область, образующаяся при пересечении кругов, соответствует логическому произведению АВ. Область, образующаяся при наложении кругов, соответствует логической сумме А + В. Часть круга А, куда не входит В, соответствует логическому произведению  . О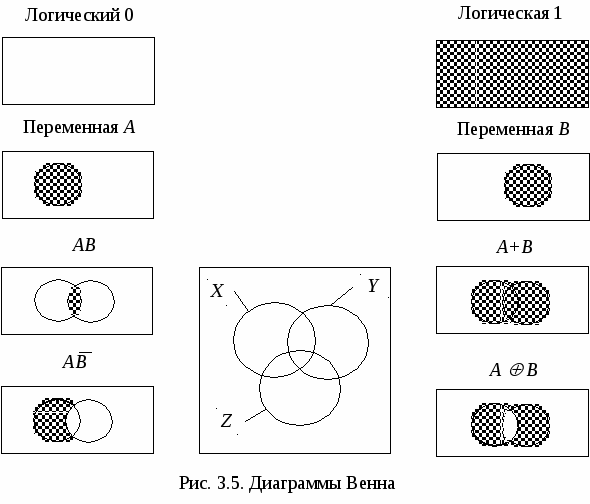перации неравнозначности соответствует область, занимаемая двумя сегментами: и  . С  помощью диаграмм Венна легко доказывается справедливость логических тождеств. Для этого надо убедиться, что левой и правой частям записанных логических выражений соответствует одинаковое отображение на диаграмме Венна. Так, при наложении круга А и сегмента АВ мы сохраняем отображение круга А, т.е. А+АВ = А. При наложении отображения A B и сегмента АВ получаем отображение логической суммы А + В, т.е. A B + АВ = А+В. Если в области А+В исключить сегмент АВ, то получим отображение операции «Исключающее ИЛИ», т.е.  (А+В) = A B.Для доказательства тождества  удобно воспользоваться диаграммой Венна для логической функции трех переменных. Если в области X+Z исключить сегмент XY, получим отображение правой части выражения. Оно совпадает с отображением левой части, получаемым путем наложения сегментов 
Для упрощения логических функций трех и четырех переменных удобно использовать карты Карно (рис. 3.6, а и 3.6, в). Карта Карно представляет собой прямоугольную таблицу, каждая клетка которой соответствует определенному набору таблицы истинности (рис. 3.6, б и 3.6, г). На карте фиксируют область прямых значений переменных и значение логической функции для каждого набора (0,1 или Х, если функция на данном наборе не определена). Карта Карно на рис. 3.6, в соответствует логической функции F, заданной выше словесно и с помощью таблицы истинности. Булева функция четырех переменных Y (рис. 3.6, а) на четырех наборах принимает значение 1, на восьми наборах – 0, на четырех наборах – не определена (такие наборы иногда называют факультативными, они обозначены как Х). 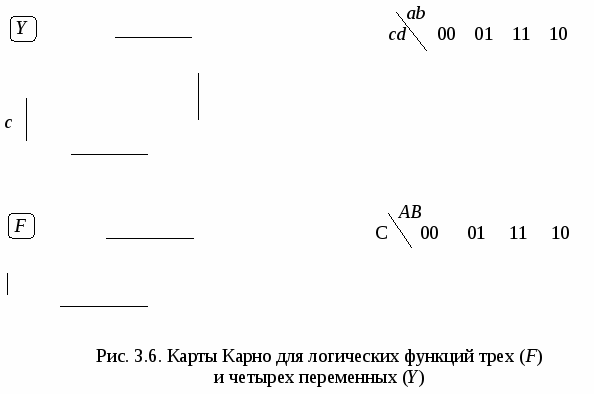 a
b A
|