Микроэлектроника

• Название: Микроэлектроника
• Анкор: Микроэлектроника.doc
• Дата: 08.04.2018
• Размер: 3.37 Mb.
• Имя файла: Микроэлектроника.doc
• Тип: Учебное пособие; #17799
• страница: 6 из 13

5.5. Преобразователи кода Грея
В преобразователях аналоговых физических величин (например, угла поворота вала) в цифровые сигналы с погрешностью, не превышающей значения младшего разряда, используется код Грея (он соответствует непозиционной системе счисления). Код Грея строится таким образом, что при переходе от одного числа к следующему изменяется всегда только один двоичный разряд. Таблица преобразования четырехразрядных двоичных чисел Х (х₄, x₃, x₂, x₁) в код Грея G(g₄, g₃, g₂, g₁) приведена ниже. Прямые и обратные преобразователи кода Грея в двоичный код реализуются с помощью логических элементов «Исключающее ИЛИ» (рис. 5.9). Код Грея не позволяет осуществлять арифметические операции. Поэтому его применяют только в тех случаях, когда это дает существенные преимущества, а затем переходят к двоичному коду.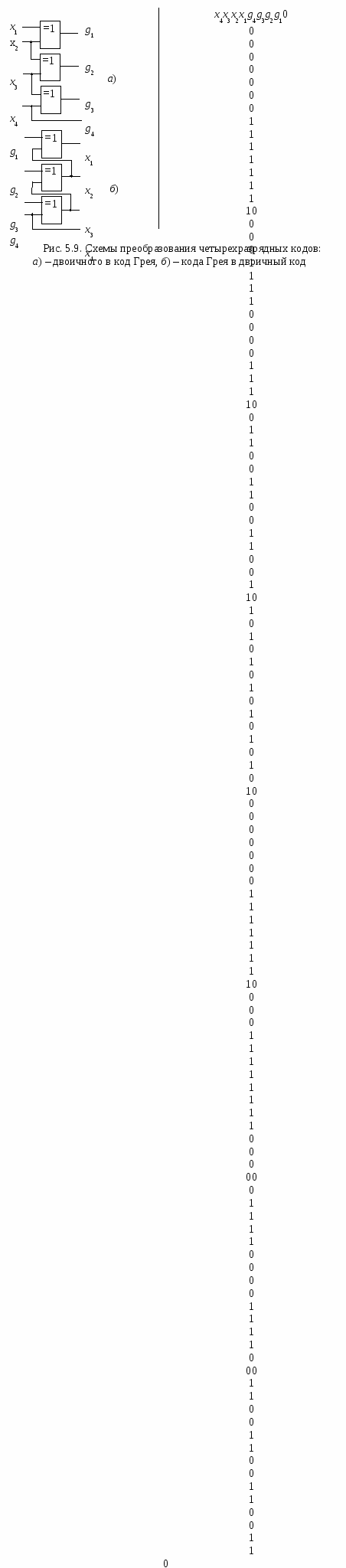




5.6. Мультиплексор
Мультиплексором (от англ. Multiplexer – многократный) называют коммутатор сигналов с нескольких входов на один выход. Для коммутатора с четырех входов Х_iна один выход Y (рис. 5.10, а) выходной сигнал связан с входными соотношением

. (5.1)

Это выражение показывает путь реализации мультиплексора на логических элементах (рис. 5.10, б).

При наличии разрешения на входе Е (Е = 1) выход повторяет информацию того входа, код которого подан на адресные входы А и В. При Е = 0 коммутатор закрыт (Y = 0 независимо от сигналов на входах Х_i).

Если цифровой код на адресных входах мультиплексора поочередно перебирает все комбинации двоичных переменных на адресных входах, состояние на выходе последовательно повторяет состояние всех его информационных входов (режим мультиплексирования данных). В этом режиме мультиплексор выполняет преобразование параллельного двоичного кода на информационных входах в последовательный код на его выходе.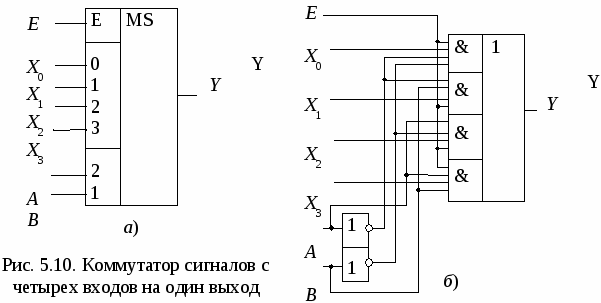




Микросхемы мультиплексоров отличаются по числу информационных и адресных входов, наличием или отсутствием входа разрешения, характером выходных сигналов (прямые, инверсные или парные).Примеры микросхем мультиплексоров серии К555 приведены на рис. 5.11.

С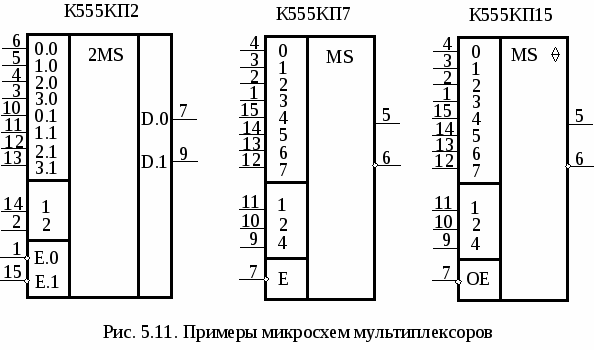
двоенный мультиплексор К555КП2 представляет собой два четырехканальных коммутатора с общим адресным дешифратором. При лог. 0, поданном на вход Е.0, на выход D.0 проходит сигнал с одного из входов 0.0 – 3.0, адрес которого зафиксирован на 2 и 14 ножке микросхемы. При лог. 0, поданном на вход Е.1, на выход D.1 проходит сигнал с одного из входов 0.1 – 3.1.

Мультиплексор К555КП7 имеет восемь информационных входов, три адресных, инверсный вход разрешения. У микросхемы два выхода – прямой и инверсный. При лог. 0 на входе Е сигнал на прямом выходе повторяет сигнал на том информационном входе, номер которого совпадает с десятичным эквивалентом кода на входах 4, 2, 1 мультиплексора. Аналогично работает и микросхема К555КП15, но подача лог. 1 на вход ОЕ переводит и прямой, и инверсный выходы в высокоимпедансное состояние.

Среди схем коммутации необходимо особо выделить устройства, которые способны пропускать сигналы в обоих направлениях. К таким элементам относятся коммутационные схемы, выполненные по технологии КМОП с использованием двунаправленных ключей. Коммутаторы КМОП способны пропускать как аналоговые, так и цифровые сигналы, в них можно менять местами вход и выход. Такие микросхемы выполняют функции мультиплексора-демультиплексора.
5.7. Реализация функций с помощью мультиплексора
Мультиплексоры удобно ис­пользовать для реализации ло­гических функций, за­писанных не­посредственно в СДНФ. Лю­бую булеву функцию че­тырех пере­менных можно реализовать с помощью восьмиканаль­ного мультип­лексора. Так, для реализации, например, логической функции

,

г
де D – переменная младшего разряда, на адресные входы мультиплексора К555КП7 поданы входные сигналы А, В, С, а входы Х0 – Х7 используются как настроечные (рис. 5.12, а). Сравнивая выражение для функции F c логическим уравнением мультиплексора



получаем условия эквивалентности:

X0 = X3 = , X7 = D, X5 = + D = 1, X1 = X2 = X4 = X6 = 0.

Эти соотношения позволяют зашифровать входы мультиплексора на выполнение заданного логического уравнения.

В соответствии с этими условиями построена схема устройства (рис. 5.12, б). Для подачи логической 1 входы микросхем ТТЛШсерий К555 и КР1533 можно подключать к источнику питания +5В непосредственно. Для получения сигнала использован инвертор.
5.8. Двоичный сумматор
Д
воичный сумматор (SM)(рис. 5.13, а) служит для формирования арифметической суммы n-разрядных двоичных чисел А и В (рис. 5.12, б). Результатом сложения (при n = 4) является четырехразрядная сумма S и выход переноса Р, который можно рассматривать как пятый разряд суммы.
П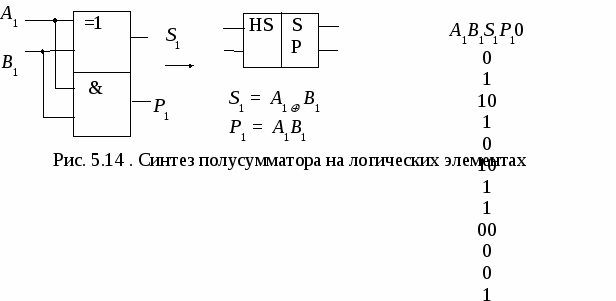
олусумматор (HS) служит для сложения битов младших разрядов двух двоичных чисел (его можно реализовать на ЛЭпо таблице истинности, представленной на рис. 5.14).
Полный одноразрядный сумматор суммирует биты соответствующих разрядов двух двоичных чисел и вырабатывает перенос в следующий разряд.

Полный одноразрядный сумматор можно построить из двух полусумматоров HS и логического элемента ИЛИ (рис. 5.15).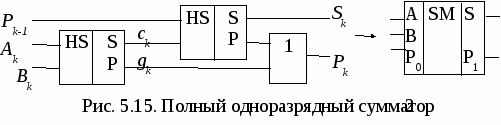


В корпусе микросхемы К555ИМ6 четыре полных одноразрядных сумматора объединены в схему четырехразрядного сумматора (рис. 5.16). Сигнал переноса последовательно передается с выхода предыдущего разряда сумматора на вход переноса следующего разряда. В дальнейшем будем использовать более простое и наглядное условное графическое обозначение сумматора, приведенное справа. В дополнительных полях микросхемы показаны весовые коэффициенты разрядов входа и выхода сумматора.

В
ремя выполнения операции в сумматоре на рис. 5.16 намного больше времени сложения в одноразрядном сумматоре, так как в каждый следующий разряд единица переноса попадает, проходя все более длинную цепочку логических элементов. Чтобы уменьшить время выполнения операции сложения многоразрядных чисел, используют схемы параллельного переноса. При этом сигналы переноса во всех разрядах одновременно вычисляются по значениям входных переменных в данном разряде.

Для сигнала переноса из любого k-го разряда справедливо соотношение (см. обозначения на рис. 5.15)
p_k = a_kb_k + (a_k  b_k)p_k-1, (5.2)



g_k с_k

где g_k- функция генерации переноса;

с_k - функция распространения переноса.
Пользуясь рекуррентным выражением (5.2), можно вывести следующие формулы для вычисления сигналов переноса в четырехразрядном сумматоре:
p₁= g₁+ p₀c₁,

p₂= g₂+ p₁c₂ = g₂+ c₂g₁+p₀c₁c₂,

p₃= g₃+ p₂c₃ = g₃ + c₃g₂+ c₂c₃g₁ + p₀c₁c₂c₃,

p₄ = g₄+ p₃c₄= (g₄+ c₄g₃+ c₃c₄g₂+ c₂c₃c₄g₁) + p₀(c₁c₂c₃c₄).




G C

Реализацию этих функций выполняет схема ускоренного переноса (см. блок-схему параллельного сумматора на рис. 5.17). Хотя полученные логические выражения достаточно сложны, время формирования сигнала переноса в любой разряд с помощью вспомогательных функций определяется временем задержки распространения сигнала в двух элементах.

Д
ля построения 16-разрядного сумматора используется эта же схема ускоренного переноса, на которую подаются сигналы G и С от каждого четырехразрядного сумматора.
5.9. Двоично-десятичный сумматор
Д
ля сложения двух двоично-десятичных чисел можно использовать по одному четырехразрядному сумматору на каждую декаду. Однако после суммирования следует производить коррекцию. Если в какой-либо декаде происходит перенос или получается двоичное число, большее 9, необходимо добавлять к ней 6, чтобы компенсировать разницу в весах разрядов. Возникающая при этом единица переноса передается в следующую по старшинству декаду (рис. 5.18).
5.10. Схемы вычитания
Вычитание двух чисел обычно сводится к операции сложения:

D = A – B = A + (2ⁿ– B) – 2ⁿ, (5.3)

где 2ⁿ– B = + 1 – дополнение В до числа 2ⁿ, которое легко получить без помощи специальных схем, использующих вычитание.

Таким образом, вычитание можно осуществить, инвертируя число В, суммируя полученный результат с А и еще с одной 1 и вычитая 2ⁿ. Вычитание 2ⁿ достигается весьма просто – путем инверсии сигнала переноса. Схема вычитания четырехразрядных чисел показана на рис. 5.19.

При А  В получаем V = 0 (в чем легко убедиться на конкретных численных примерах). При A < B получаем V = 1 и число D является дополнением А – В до 2⁴ = 16. Выходной сигнал можно рассматривать как пятиразрядное число со знаком V в дополнительном коде.

На рис. 5.20 показано устройство, которое используется в цифровых следящих системах для выделения сигнала рассогласования между кодом задатчика А и кодом сигнала обратной связи В. Знак sign(A – B) определяет направление компенсирующего воздействия на регулирующий орган, а модуль разности (А – В) R (r₀ – r₇) – скорость этого воздействия. Наличие нулей во всех разрядах А соответствует одному крайнему значению регулируемой величины, а единиц – другому.



При А > B появляется единица на выходе переноса сумматора, в знаковом разряде 0, а (здесь плюс – знак арифметического сложения). Элементы «Исключающее ИЛИ» работают как повторители выходных сигналов сумматора.

При A B в старшем разряде сумматора 0 (читателю предлагается проверить это на конкретном численном примере). Знак равен 1, а Элементы «Исключающее ИЛИ» работают как инверторы выходных сигналов сумматора.

Выходной сигнал устройства можно рассматривать как девятиразрядное двоичное число со знаком в прямом коде.

Обычный сумматор может использоваться для сложения чисел со знаком, представленных в дополнительном коде. На его выходе формируется дополнительный код суммы. При сложении, например, 8-разрядных двоичных чисел со знаком с помощью 8-разрядного сумматора (его можно построить на двух микросхемах К555ИМ6) получаем на выходе 8-разрядную сумму в дополнительном коде (перенос в 9-й разряд игнорируется). При этом разрядная сетка не должна переполняться, т.е. сумма модулей для чисел одинакового знака не должна превышать 127. Старший разряд восьмиразрядных слагаемых отображает знак числа (0 – для положительного, 1 – для отрицательного). Семь младших разрядов отображают модуль числа. Дополнительный код положительного числа соответствует его обычному представлению в двоичном коде. Для получения дополнительного кода отрицательного числа нужно проинвертировать код положительного числа и прибавить единицу в младший разряд. Приведенный ниже пример показывает, что при подаче на входы сумматора дополнительных кодов чисел +100 и –16, на выходе получим код числа + 84.
01100100

11110000

101010100 = +84

девятый разряд игнорируется результат положительный

5.11. Преобразователь прямого кода в дополнительный
Для преобразования в дополнительный код 8-разрядных чисел со знаком, представленных в прямом коде, используется изображенное на схеме рис. 5.21 устройство. Для положительных чисел знаковый разряд х₇= 0, элементы«Исключающее ИЛИ» и сумматор работают как повторитель числа Х. Для отрицательных чисел х₇= 1, семиразрядный модуль числа Х инвертируется и к нему с помощью сумматора прибавляется 1. Такое же устройство используется и как преобразователь дополнительного кода числа в прямой.

5
.12. Цифровой компаратор
Ц
ифровым компаратором называют устройство, фиксирующее результат сравнения n-разрядных двоичных или двоично-десятичных кодов чисел (рис. 5.22, а). Цифровой компаратор можно построить на сумматоре, подавая на один суммирующий вход прямой код числа А, на другой – инверсный код числа В (рис. 5.22, б). На численном примере легко убедиться, что при А = В в четырех младших разрядах суммы формируются логические единицы, а при A > B единица формируется на выходе переноса.

Компаратор, фиксирующий равнозначность кодов А и В, можно выполнить на ЛЭ по схеме, показанной на рис. 5.23, а. При совпадении кодов во всех разрядах формируются логические нули на выходах элементов «Исключающее ИЛИ» и логический элемент ИЛИ-НЕ формирует на выходе 1. Другой вариант построения схемы равнозначности кодов приведен на рис. 5.23, б.

5.13. Контроль четности
Контроль четности (нечетности) используется для обнаружения однократных ошибок при передаче данных по линиям связи (рис. 5.24). В передатчике к n-разрядному слову добавляется контрольный разряд (бит паритета) с таким значением (0 или 1), чтобы сумма единиц в (n + 1)-разрядном сообщении была бы четной. В приемнике производится контроль на четность. Если число единиц в принятом слове нечетно, фиксируется ошибка при передаче данных.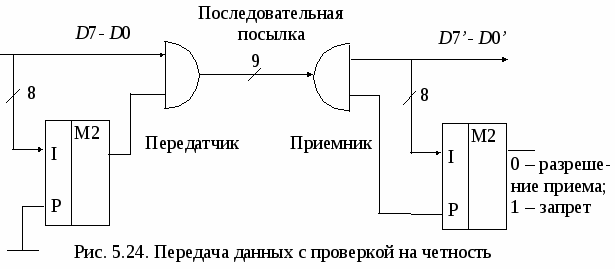




Для контроля восьмиразрядного сообщения можно использовать микросхему К555ИП5 – сумматор по модулю два. Он содержит внутри восемь логических элементов «Исключающее ИЛИ». В передатчике 9-разрядное сообщение преобразуется в последовательный код (это преобразование можно выполнить с помощью регистра сдвига), передается по одному каналу связи, а затем на стороне приемника подвергается обратному преобразованию в параллельный код. Если число единиц в принятом сообщении четно, логический 0 на выходе К555ИП5 разрешает прием сообщения D7’- D0’. В противном случае на выходе сумматора по модулю два формируется лог. 1и прием сообщения запрещается. Функциональная схема и логическая структура микросхемы К555ИП5 приведены на рис. 5.25.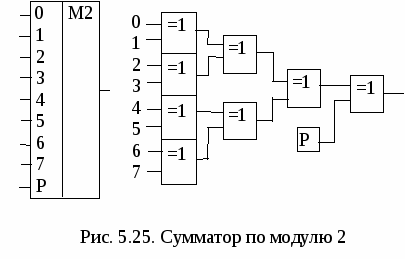