Микроэлектроника
 Скачать 3.37 Mb. Скачать 3.37 Mb.
|
|
B Карта Карно определяет значение функции на всех возможных наборах аргументов и, следовательно, является копией таблицы истинности. Карты Карно компактны и удобны для поиска склеиваемых членов переключательной функции СДНФ. Объясняется это тем, что два любых минтерма, находящихся в клетках, расположенных рядом друг с другом, являются соседними. Они могут быть заменены одной конъюнкцией, содержащей на одну переменную меньше. Группа из четырех минтермов, расположенных в соседних клетках, может быть заменена конъюнкцией, содержащей на две переменные меньше. В общем случае группа из 2k соседних клеток будет заменена одной конъюнкцией с n – k аргументами при общем числе переменных, равном n. Правила записи минимизированного выражения для логической функции по карте Карно: 1) выделяются блоки (замкнутые прямоугольные области, содержащие 1, 2, 4 , 8 клеток), заполненные единицами; 2) блоки должны быть возможно большими, а их количество наименьшим; 3) левая и правая, а также верхняя и нижняя строки карты считаются соседними; 4) блоки могут пересекаться, т.е. одна и та же клетка может входить в несколько блоков; 5) на факультативных наборах функция может доопределяться произвольно (на тех наборах, где стоят Х), чтобы получить наиболее крупные блоки; 6) функция записывается в виде суммы логических произведений (ЛП), описывающих выделенные блоки; 7) переменная не включается в ЛП, если блок областью ее прямых значений делится пополам; 8) переменная включается в ЛП с инверсией, если рассматриваемый блок лежит в области ее инверсных значений; 9) при группировке в блоки клеток, заполненных нулями, по тем же правилам получаем инверсное значение логической функции. Логическая функция F(см. рис. 3.6)описывается совокупностью трех блоков (каждый блок включает группу из двух минтермов): F = AB + BC + AC. (3.3) С использованием формулы двойственности ее можно преобразовать в вид, удобный для реализации в базисе И-НЕ (рис. 3.7, а): Логическая функция четырех переменных Y описывается совокупностью двух блоков (четыре угловые клетки считаются соседними): На рис. 3.7, б приведен пример ее реализации, учитывающий преобразование к виду 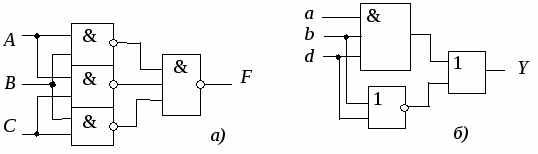 Рис. 3.7. Реализация логических функций F и Y
При синтезе комбинационного цифрового устройства на логических элементах можно рекомендовать следующий порядок: 1) формируется словесное условие задачи (определяется, что именно должно делать разрабатываемое устройство, уточняется алгоритм его работы); 2) составляется таблица истинности для логической функции, реализуемой устройством, и записывается функция в СДНФ; 3) проводится минимизация логической функции с помощью карты Карно, диаграммы Венна или законов булевой алгебры; 4) функция преобразуется в вид, удобный для реализации на заданной элементной базе; 5) разрабатывается принципиальная схема цифрового устройства на логических элементах выбранной серии интегральных микросхем. Микросхемы логических элементов будут рассмотрены в следующей главе. Результат синтеза не является однозначным, поэтому вариантов построения цифрового устройства может быть несколько. Следует стремиться к более простому решению поставленной задачи. В следующем параграфе рассмотрены примеры синтеза комбинационных цифровых устройств на логических элементах ТТЛ (серия К155) и ТТЛШ (серия К555). При проектировании таких устройств надо четко представлять, каким образом формируются входные сигналы и как используются выходные сигналы.
Пример 3.5.Реализовать устройство с четырьмя входами, логическая функция которого задана таблицей истинности (рис. 3.8, в). 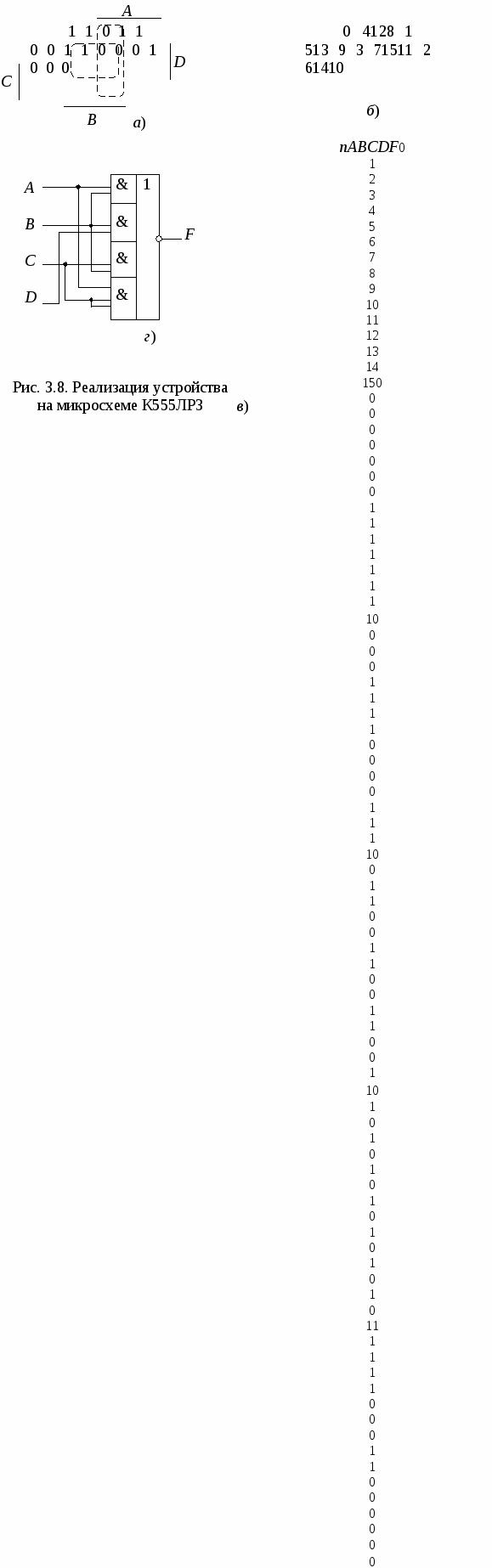 Решение. Представим логическую функцию, реализуемую устройством, в виде соответствующей ей карты Карно (рис. 3.8, а). На рис. 3.8, б представлена таблица соответствия ее клеток наборам таблицы истинности. Организовав блоки по нулям (блоки АВ и BD выделены на карте Карно пунктирной линией), запишем минимизированное выражение для логической функции по карте Карно: которое легко реализовать на микросхеме К555ЛР3 (рис. 3.8, г). Если блоки организовать по единицам, то их число уменьшается до трех, но требуются дополнительные инверторы: Пример 3.6.На микросхемах серии К155 спроектировать утроитель частоты напряжения трехфазной сети. Напряжение каждой фазы с помощью нуль-компараторов приведено к уровню ТТЛ (входной сигнал равен логической 1, когда синусоидальное напряжение фазы положительно). Решение. Алгоритм работы устройства отображают временные диаграммы входных (А, В, С) и выходного (F) сигналов для одного периода T сетевого напряжения (рис. 3.9, а). Заполним карту Карно для единичных и нулевых тактов сигнала F (рис. 3.9, б). На двух наборах функция не определена (в трехфазной сети напряжения трех фаз не могут быть одновременно положительными или отрицательными). Организуя блоки по нулям, получаем 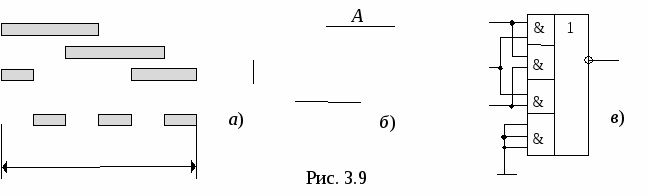
|
