Методичка 2020. МетодичкаТВ_и_МС_2020. Миниобранауки россии

• Название: Миниобранауки россии
• Анкор: Методичка 2020
• Дата: 30.12.2022
• Размер: 1.04 Mb.
• Имя файла: МетодичкаТВ_и_МС_2020.doc
• Тип: Курсовая; #869818
• страница: 2 из 8

1. РАСЧЕТ ОСНОВНЫХ ПОКАЗАТЕЛЕЙ СТАТИСТИКИ

Показатели описательной статистики можно разбить на несколько групп.

1. Показатели положения описывают положение данных на числовой оси. Примеры таких показателей: минимальный и максимальный элементы выборки (первый и последний члены вариационного ряда), верхний и нижний квартили (ограничивают зону, в которую попадают 50% центральных элементов выборки), средняя арифметическая, средняя гармоническая, медиана и другие характеристики.

2. Показатели разброса описывают степень разброса данных относительно своего центра. К этой группе относятся: дисперсия, стандартное отклонение, размах выборки (разность между максимальным и минимальным элементами), межквартильный размах (разность между верхней и нижней квартилью), эксцесс и т.п. Эти показатели определяют, насколько кучно основная масса данных группируется около центра.

3. Показатели асимметрии характеризуют симметрию распределения данных около своего центра. К ним можно отнести коэффициент асимметрии, положение медианы относительно среднего и т.п.

4. Показатели, описывающие закон распределения, дают представление о законе распределения данных. Сюда относятся таблицы частот, таблицы частостей, полигоны, кумуляты, гистограммы.

На практике чаще всего используются следующие показатели: средняя арифметическая, медиана, дисперсия, стандартное отклонение.
Расчёт показателей описательной статистики

1. Среднее.

Функция СРЗНАЧ рассчитывает значение средней арифметической величины по формуле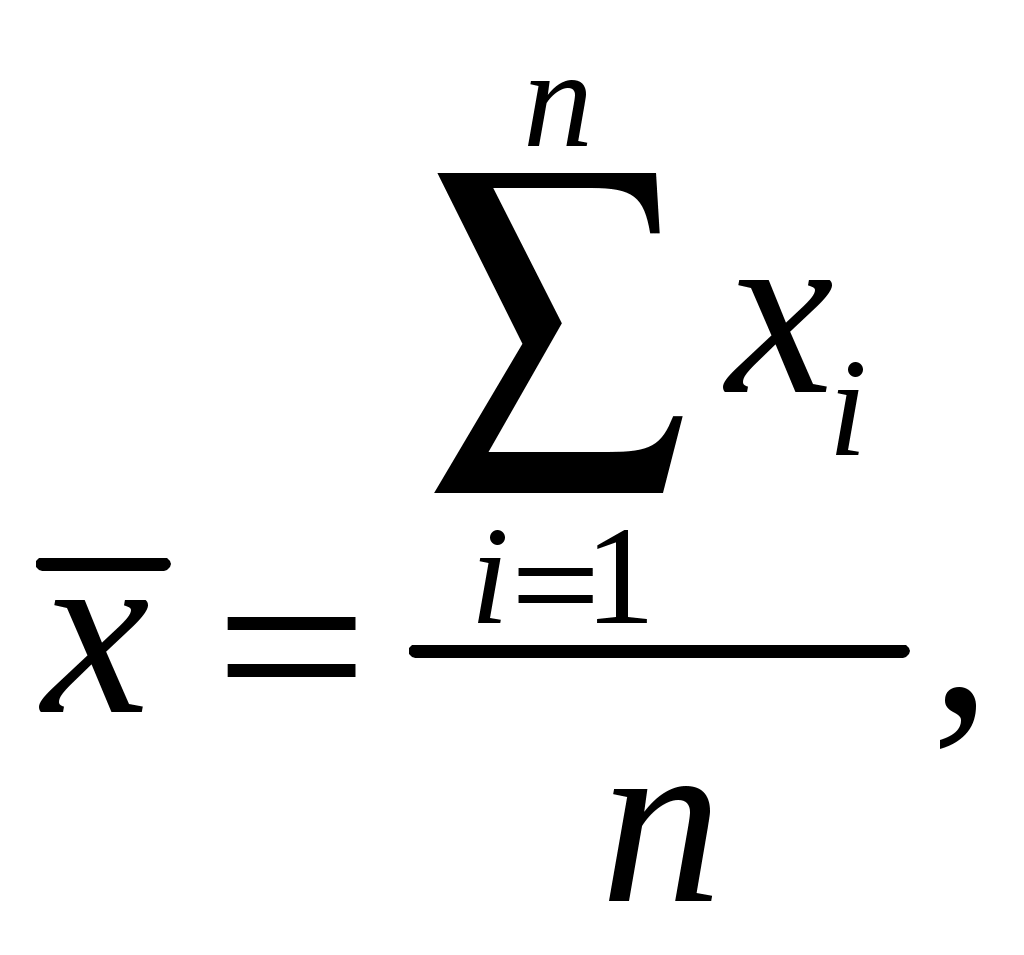



где x_i – i-ое значение выборки, n – число наблюдаемых значений выборки.

2. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Используется функция МЕДИАНА.

3. Модой (Мо) называется чаще всего встречающаяся варианта или то значение признака, которое соответствует максимальной точке теоретической кривой распределения. Используется функция МОДА.

4. Выборочная дисперсия рассчитывается по выборочным данным. Для этого используется выражение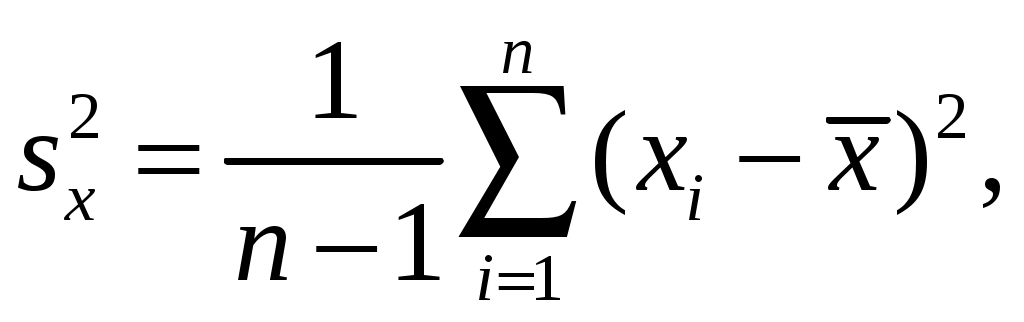



где – среднее арифметическое выборки.

Для определения в Excel можно воспользоваться функцией ДИСП.

5. Выборочное стандартное отклонение оценивает разброс возможных значений случайной величины вокруг её среднего. Формула для расчета стандартного отклонения



Для определения в Excel можно воспользоваться функцией СТАНДОТКЛОН.

6. Стандартная (средняя) ошибка повторной собственно-случайной выборки определяется по формуле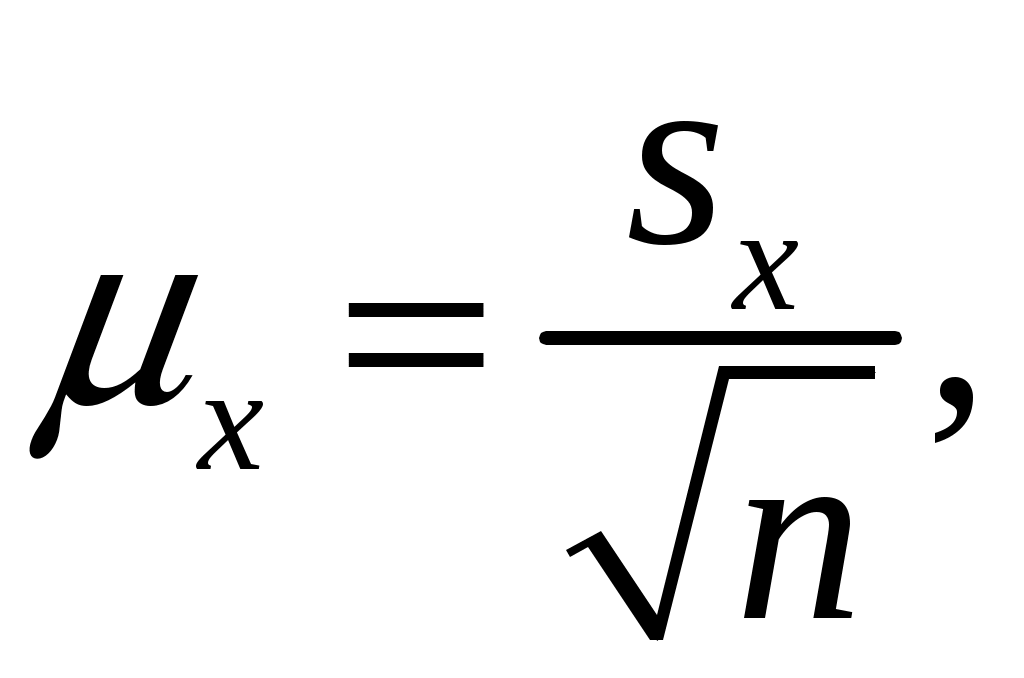



где s_x – выборочная дисперсия, n – число наблюдаемых значений выборки.

7. Эксцесс характеризует так называемую «крутость», т.е. островершинность или плосковершинность кривой распределения. За исходную принята кривая нормального распределения (E_k = 0), если E_k > О, распределение островершинное, если E_k < 0 – плосковершинное.

Для определения в Excel можно воспользоваться функцией ЭКСЦЕСС, которая рассчитывает значение эксцесса как для симметричных, так и для асимметричных распределений.

8. Симметричным является распределение, в котором частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. С учетом этого показатель асимметрии основан на соотношении показателей центра распределения: чем больше разница между х, Mo, Me, тем больше асимметрия ряда. При этом если Mo < Me, асимметрия правосторонняя, если Mo > Me – асимметрия левосторонняя.

Функция СКОС определяет величину асимметрии по выборочной совокупности. При этом если A_s > О – асимметрия правосторонняя (положительная), если A_s < О — асимметрия левосторонняя

9. Функции МИН и МАКС используются для определения минимального и максимального значений признака в выборке.

10. Интервалрассчитывают как разность между наибольшим (х_mах) и наименьшим (х_min) значениями выборки, т.е.

R = x_max– x_min

и называется размах вариации.

11. Функция СЧЕТ используется для определения величины n.

12. Функции НАИБОЛЬШИЙ и НАИМЕНЬШИЙ определяют k-ое максимальное и минимальное значения в выборке.

13. Уровень надёжности.

Предельная ошибка выборки связана со средней ошибкой выборки соотношением



где t – коэффициент доверия, который определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования.

В Excel коэффициент доверия t рассчитывается через функцию СТЬЮДРАСПОБР, в которой в качестве аргументов задаются уровень значимости a и число степеней свободы df. Уровень значимости a связан с доверительной вероятностью b выражением

a = 1 – b.

Число степеней свободы df зависит от объема выборки n и связано с ним выражением df = n – 1.

Границы доверительного интервала для математического ожидания находятся из выражения




ЗАДАНИЕ:

1. 
   Сгенерировать 100 значений нормально распределенной случайной величины с параметрами m_x, σ_x
   
2. 
   Рассчитать значения показателей описательной статистики.
   
3. 
   Рассчитанные значения свести в таблицу вида
   

№	Показатель	Значение
1	…	…
2	…	…