Методичка 2020. МетодичкаТВ_и_МС_2020. Миниобранауки россии
 Скачать 1.04 Mb.
|
4. Проверка гипотезы о равенстве средних величин при известной дисперсииИногда оказывается, что средний результат  из основной серии опытов отличается от среднего результата  другой серии опытов. Необходимо определить случайно или нет, это различие, т.е. можно ли считать, что результат эксперимента представляет собой выборка из двух независимых генеральных совокупностей с одинаковыми средними, или средние этих совокупностей не равны.Формальная постановка этой задачи выглядит следующим образом – изучаются две случайные величины, распределённые по нормальному закону: 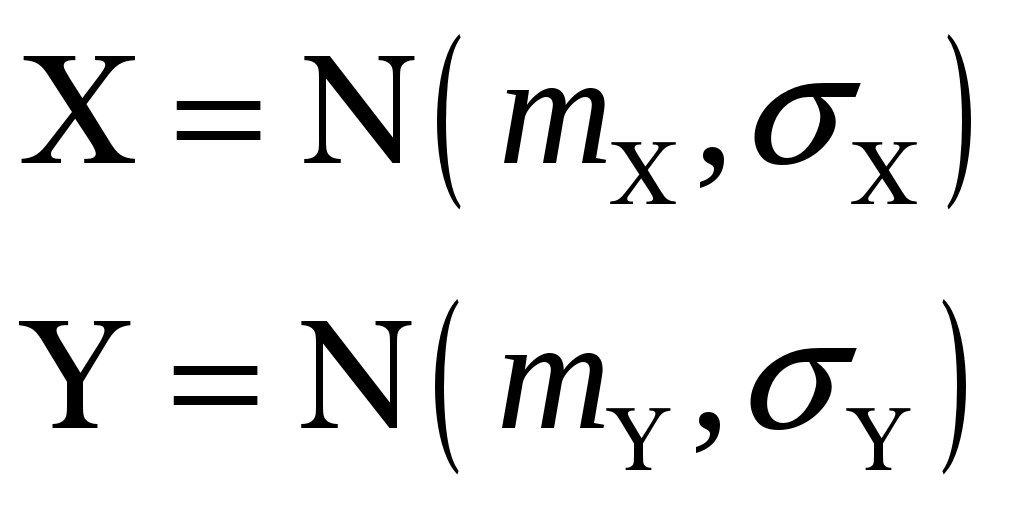 ,где σ – стандартное отклонение, m – математическое ожидание (среднее). Предполагается, что дисперсии  и  известны, а математические ожидания не известны. Пусть имеются две серии наблюдений величины Χ и Υ. Χ: х1, х2, …, хn1. Υ: y1, y2, …, yn2. Выдвигаем следующую гипотезу, что mx= my. На основании наблюдений необходимо подтвердить или опровергнуть эту гипотезу. Если подтвердится нулевая гипотеза, то можно говорить о том, что различия между средними величинами в двух выборках статистически незначимо, т.е. объясняется как случайной ошибкой. Для проверки этой гипотезы используется Z-тест. Для этого рассчитывается z-критерий (z-статистика), который определяется следующим образом: 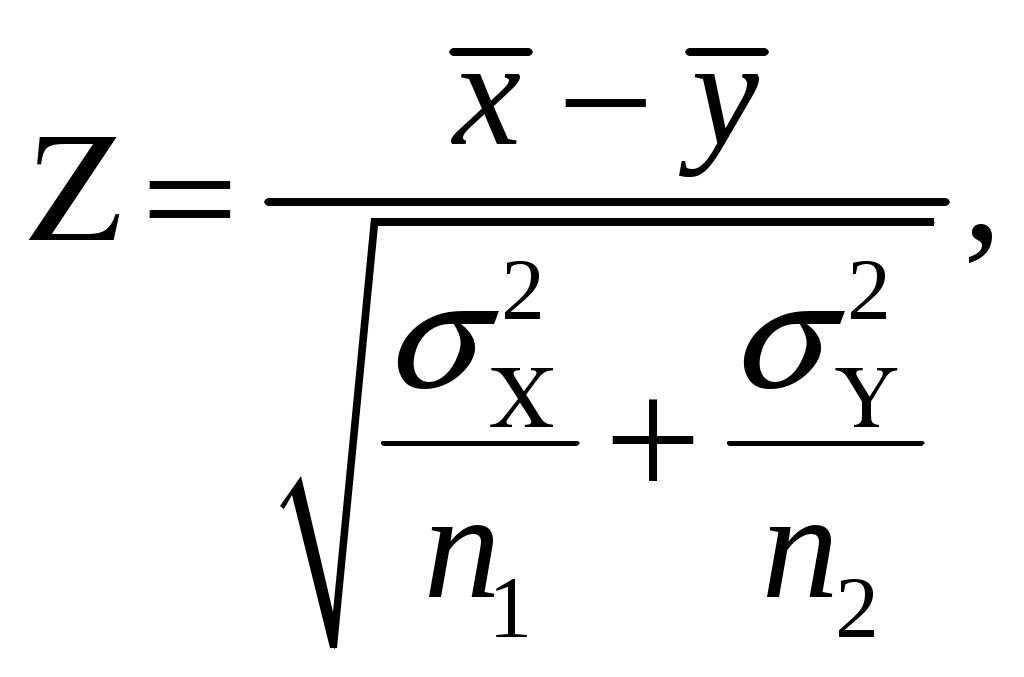 где 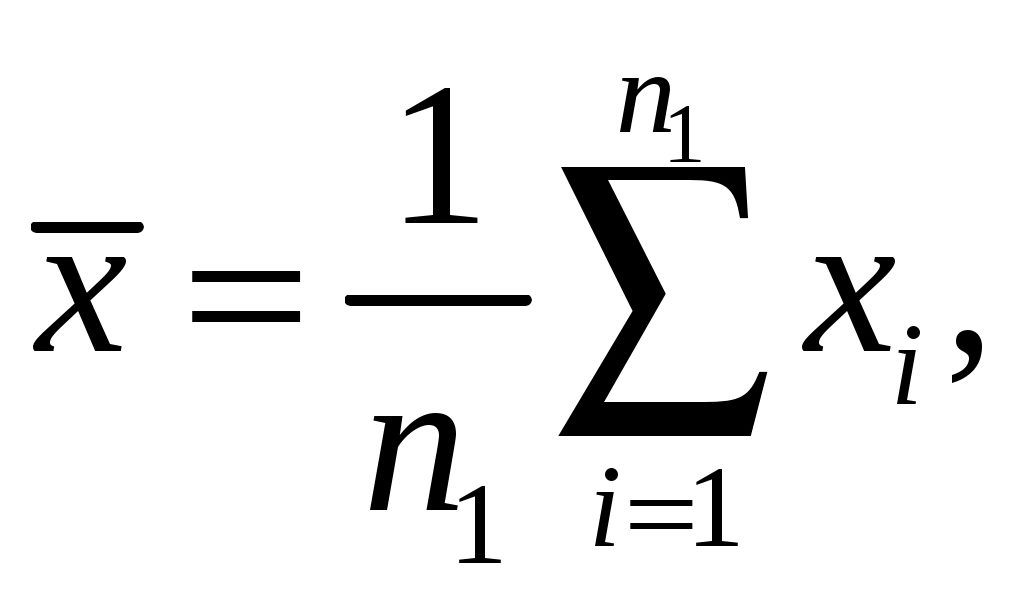 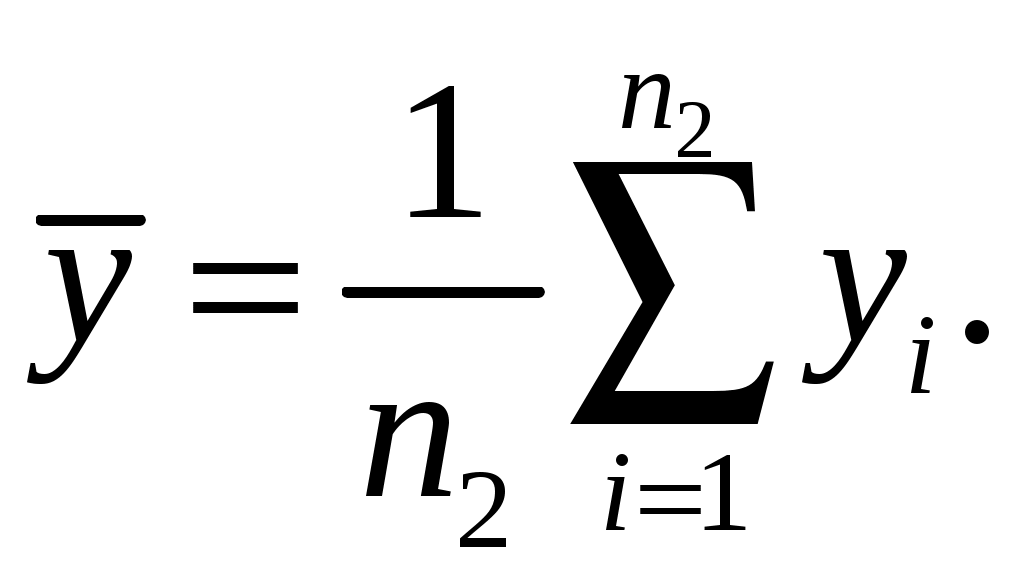– среднее арифметическое значение из серии nнаблюдений.  Z-критерий распределён нормально с нулевым математическим ожиданием и единичной дисперсией. Нулевая гипотеза:  .Альтернативная гипотеза:  Последовательность проведения тестирования: Вычисляем статистику Z. Задаёмся уровнем значимости  .Определяем критические точки. Сравниваем рассчитанное в п.1 значение Zсо значением критических точек: Если значение Z-статистики будет по абсолютной величине больше чем значение критической точки, то нулевая гипотеза отклоняется при данном уровне значимости . Это означает, что две совокупности, из которых сделана выборка, различны и, следовательно, средние значения и математические ожидания для этих выборок не равны. В противном случае принимается нулевая гипотеза о равенстве средних значений, и можно рассматривать эти две совокупности как одну общую с одним и тем же математическим значением.ЗАДАНИЕ. Сгенерировать 2 нормально распределенные переменные. Первая переменная генерируется в соответствии с Вашим вариантом. При генерации второй переменной математическое ожидание увеличивается на 2, а стандартное отклонение на 0,5 Проверить гипотезу о равенстве средних аеличин 5. Проверка гипотезы о равенстве дисперсийДля того чтобы определить на основе выборочных данных равны ли дисперсии или нет, мы рассмотрим процедуру проверки гипотезы о равенстве дисперсий двух независимых нормально распределённых случайных величин. Эта задача имеет также самостоятельное значение, поскольку дисперсия характеризует точность работы приборов или технологических процессов, обработки данных и т.п. Убедившись в равенстве двух дисперсий, мы тем самым убеждаемся, например, в том, что два прибора обеспечивают одинаковую точность. В математической статистике доказывается, что если гипотеза о равенстве дисперсий двух случайных величин выполняется: H0: 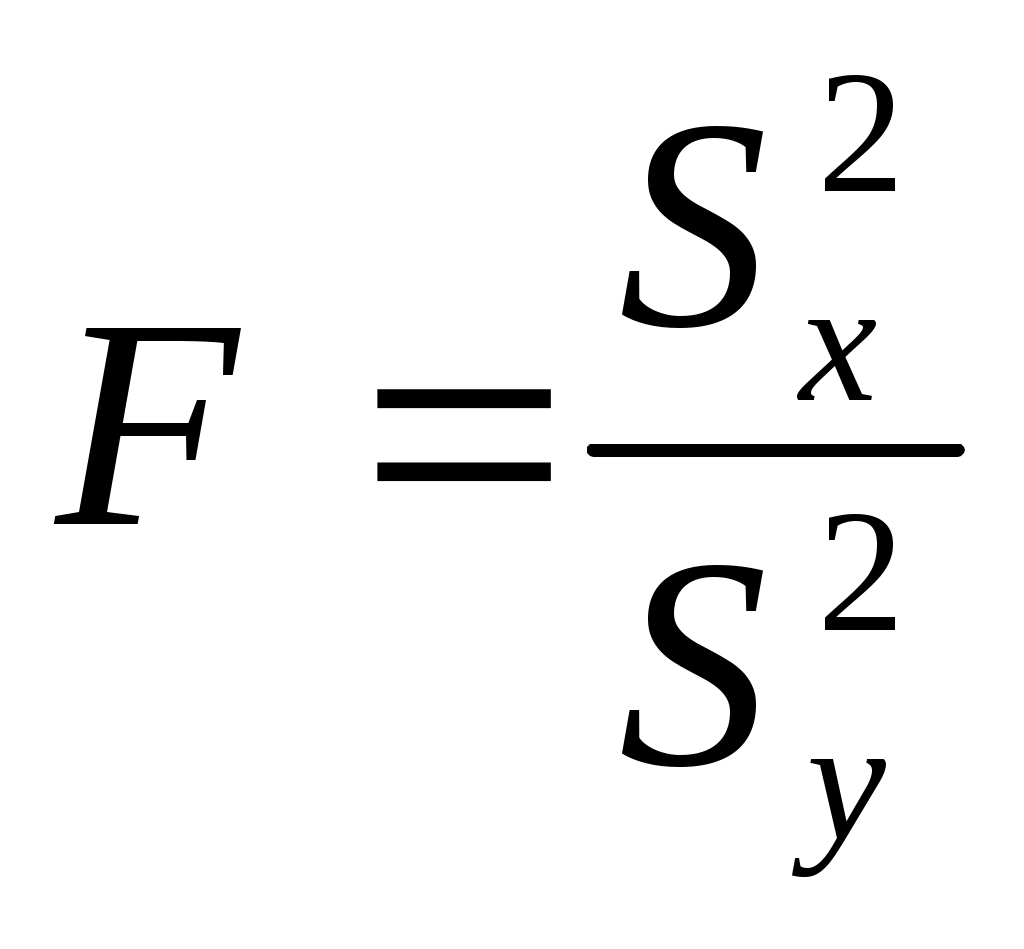= , то величина  распределена в соответствии с законом распределения Фишера. Это отношение F называют дисперсионным отношением Фишера и используют в качестве критерия проверки нулевой гипотезы. Распределение Фишера характеризуется наличием степеней свободы, которые вычисляются по формулам: 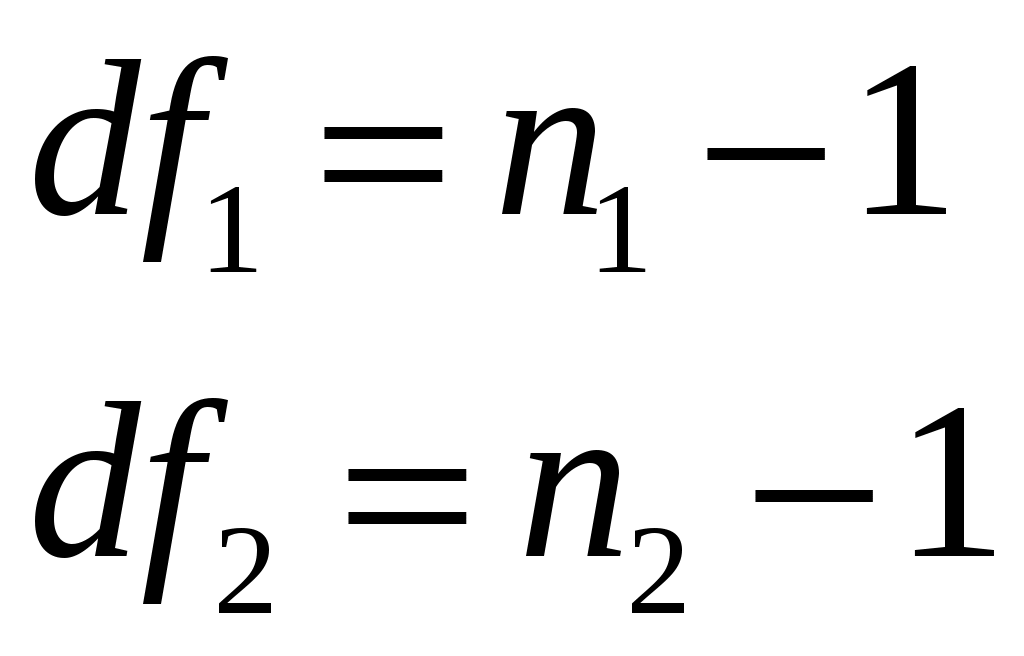 Поскольку величина F – неотрицательная, то критическая область данной величины будет принадлежать интервалу (0;+¥). Альтернативными являются гипотезы: Н1: > при  > Н1: < при < Если удвоенное значение р – уровня будет больше, чем уровень значимости (0,05) то нулевая гипотеза о равенстве дисперсий не отклоняется ЗАДАНИЕ. Используя данные задания 4 проверить гипотезу о равенстве дисперсий |