Методичка 2020. МетодичкаТВ_и_МС_2020. Миниобранауки россии

• Название: Миниобранауки россии
• Анкор: Методичка 2020
• Дата: 30.12.2022
• Размер: 1.04 Mb.
• Имя файла: МетодичкаТВ_и_МС_2020.doc
• Тип: Курсовая; #869818
• страница: 7 из 8

Поскольку F_расч = 0,2067 < 3,2388, нулевая гипотеза о равенстве дисперсий не отклоняется. Между дисперсиями внутри каждой группы существенной разницы нет, т. е. условие об однородности данных выполняется .

Для проведения однофакторного дисперсионного анализа существует инструмент в пакете анализа Excel, который так и называется « Однофакторный дисперсионный анализ».

Здесь задаются следующие параметры:

1. 
   входной интервал (вводится вся таблица с исходными данными);
   
2. 
   вид группирования (по столбцам/ по строкам);
   
3. 
   метки;
   
4. 
   поле ;
   

указать выходной интервал

Результаты анализа для примера (табл.5), приведенного выше, выведены в таблицу


Таблица 5

Однофакторный дисперсионный анализ
ИТОГО
Группы	Счет	Сумма	Среднее	Дисперсия
Поставщик 1	5	97,6	19,52	7,237
Поставщик 2	5	121,3	24,26	3,683
Поставщик 3	5	114,2	22,84	4,553
Поставщик 4	5	105,8	21,16	8,903
ДИСПЕРСИОННЫЙ АНАЛИЗ
Источник вариации	SS	df	MS	F	P-значение	F крит.
Между группами	63,2855	3	21,09516667	3,461628925	0,0413656	3,238866952
Внутри групп	97,504	16	6,094
Итого	160,7895	19

Поскольку F_расч = 3,4616крит=3,2388, гипотезу о равенстве средних величин H₀: m₁=m₂= m₃ =m₄ отклоняется в пользу гипотезы H₁.

При обнаружении значительных различий между математическими ожиданиями необходимо определить, какие именно группы отличаются друг от друга. Для этого используется процедура множественного сравнения Тьюки – Крамера, описанная ниже.

1. 
   Вычисляются разности , где i ≠ j – номера групп, между средними значениями c(c – 1) групп;
   
2. 
   Вычисляется критический размах процедуры Тьюки – Крамера по формуле
   

где Q_u –верхнее критическое значение распределения стьюдентизированного размаха, имеющего c степеней свободы в числителе df₁ = c и df₂ = n степеней свободы в знаменателе, n-общее число наблюдений, n₁ и n₂ число наблюдений в i-ой и j-ой группах соответственно.

3. 
   Каждая из c(c – 1)/2 пар разностей математических ожиданий сравнивается с рассчитанным критическим размахом.
   

Элементы пары считаются значительно различными, если модуль разности между ними превышает критический размах. Результаты расчетов приведены ниже.

	Absolute	Std. Error	Critical
Comparison	Difference	of Difference	Range	Results
	4,74	1,10399275	4,4712	Means are different
	3,32	1,10399275	4,4712	Means are not different
	1,64	1,10399275	4,4712	Means are not different
	1,42	1,10399275	4,4712	Means are not different
	3,1	1,10399275	4,4712	Means are not different
	1,68	1,10399275	4,4712	Means are not different

Таблица стьюдентизованного распределения Q_u κ=df₁, ν=df₂.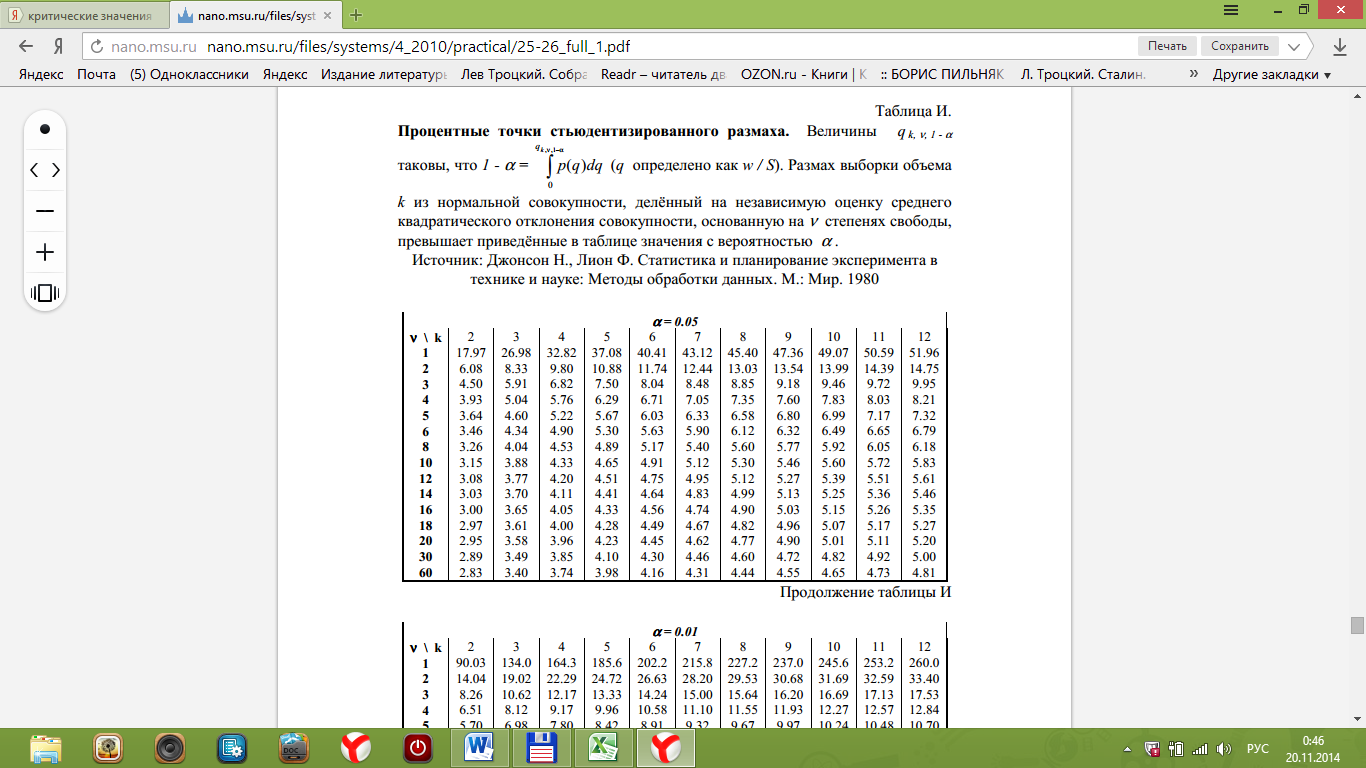


ЗАДАНИЕ

1. 
   Сгенерировать 4 нормально распределенные переменные. Первые 3 переменные генерируется в соответствии с Вашим вариантом. При генерации четвертой переменной математическое ожидание увеличивается на 2, а стандартное отклонение не изменяется
   

2. 
   Используя модифицированный критерий Левенэ проверить гипотезу о равенстве дисперсий.
   

3. 
   . Используя инструмент анализа « Однофакторный дисперсионный анализ» проверить гипотезу о равенстве математических ожиданий.
   

4. 
   При обнаружении значительных различий между математическими ожиданиями необходимо определить, какие именно группы отличаются друг от друга, используя процедуру множественного сравнения Тьюки – Крамера
   

8. ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

Простая линейная регрессия используется для исследования зависимости двух переменных. Уравнение простой линейной регрессии можно записать в виде

y_i = a₀ + a₁x_i + _i(1)

где ₁,…_n- независимые одинаково распределенные случайные величины, определяющие действие различных неучтенных факторов на изменение результирующего показателя Y.

Для определения оценок параметров в уравнении (1) широко используется метод наименьших квадратов (МНК), суть которого заключается в следующем.

Определим величину e_i следующим образом:

e_i = y_i – (a₀ + a₁x_i).

Величина e_i называется отклонением (остатком) наблюдаемого значения результирующей переменной y_i в i – ом наблюдении от расчетного. Отклонение e_i является оценкой случайной компоненты _i. По­строим оценку параметров (a₀, a₁) так, чтобы сумма их квадратов отклонений была минимальной: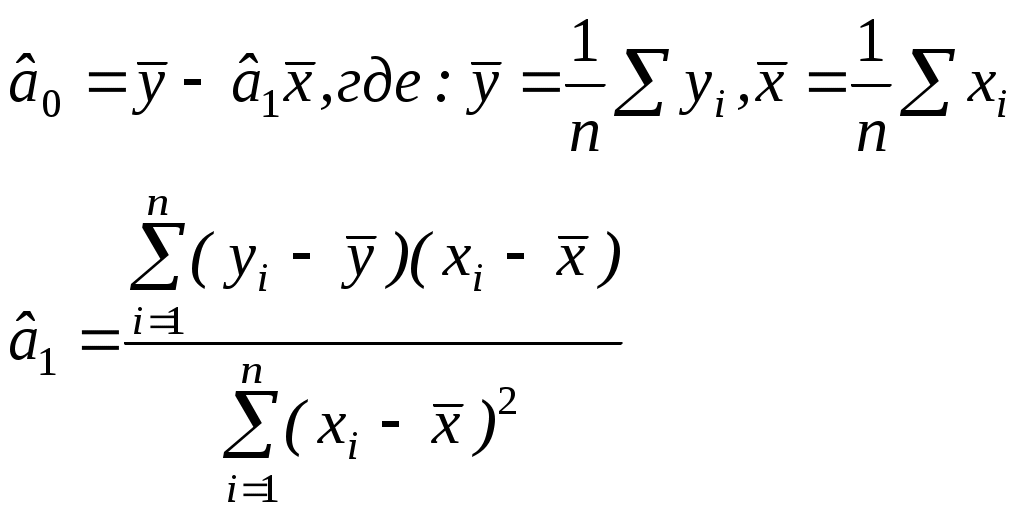

(2)

Сумму минимизируем по (a₀, a₁),приравнивая нулю соответствующие производные.В результате получим систему уравнений линейных относительно a₀ и a₁. Ее решение легко находится:

(3) и (4)

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_yx. Для линейной регрессии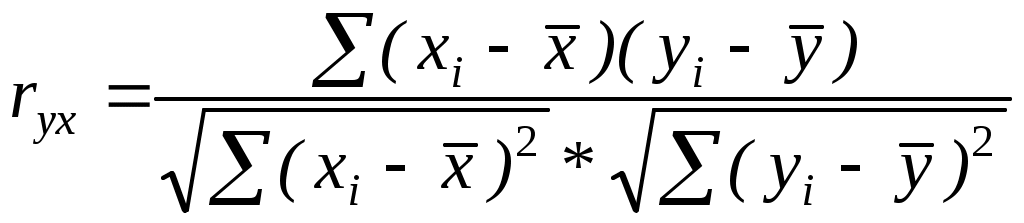
,
Степень тесноты связи результирующей и факторных переменных можно оценить, используя шкалу Чеддока

Значение ryx	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 - 0,99
Степень связи	слабая	умеренная	заметная	высокая	очень высокая

Для определения статистической значимости показателя тесноты связи и существенности связи между результирующей и факторными переменными проводится дисперсионный анализ. Задача состоит в исследовании дисперсии результирующего показателя.

Проверка гипотезы о существенности связи результирующей и факторных переменных в уравнения регрессии (статистической значимости множественного коэффициента корреляции) осуществляется с помощью F-критерия Фишера.

Для проверки вычисляется F-статистика:



где :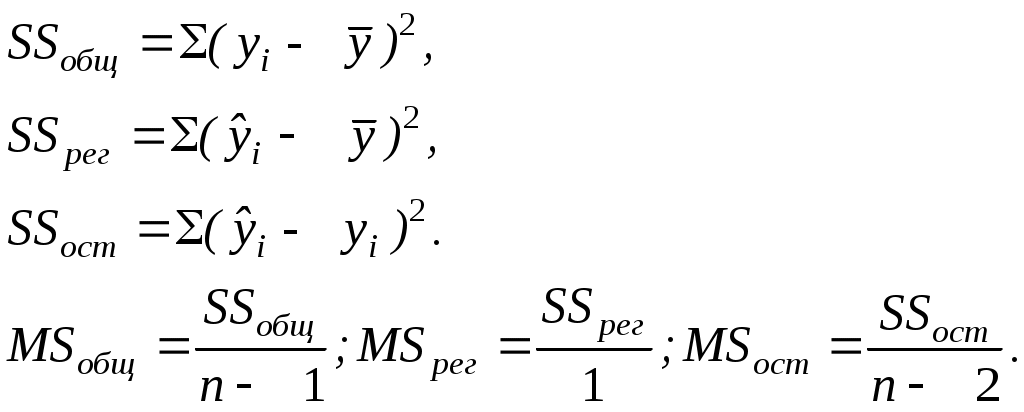



Здесь

- наблюдаемые значения y;

- значения y, вычисленные при соответствующих значениях x;

- среднее значение y.

Из таблиц распределения Фишера определяется критическое значение F_df1,df2,α при заданном уровне значимости α и степенях свободы df₁ = 1, df₂ = n-2, где уровень значимости α – вероятность совершения ошибки первого рода.

Если F_pасч> F_{df1,df2,α ,} то полученное значение множественного коэффициента корреляции можно считать статистически значимым. В противном случае полагаем r_yx = 0, что свидетельствует об отсутствии линейной зависимости между результирующей и факторными переменными в уравнения регрессии
Дисперсионный анализ

Для определения статистической значимости показателя тесноты связи и существенности связи между результирующей и факторными переменными проводится дисперсионный анализ. Задача состоит в исследовании дисперсии результирующего показателя.

Проверка гипотезы о существенности связи результирующей и факторных переменных в уравнения регрессии (статистической значимости множественного коэффициента корреляции) осуществляется с помощью F-критерия Фишера. Величина F-критерия связана с коэффициентом детерминации R²:

.

Проверка существенности связи в уравнения регрессии с помощью F-критерия проводится при условии нормальности распределения ошибки регрессии.

Для проверки вычисляется F-статистика:



где :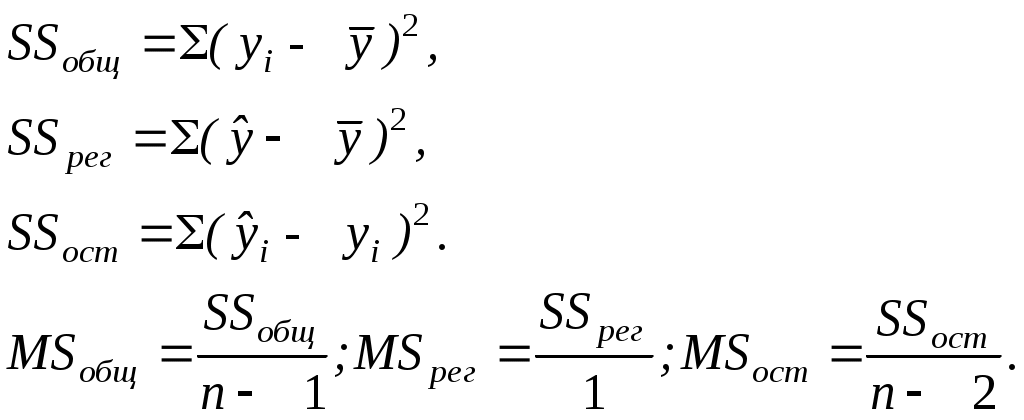



Из таблиц распределения Фишера определяется критическое значение F_df1,df2,α при заданном уровне значимости α и степенях свободы df₁ = 1, df₂ = n-2, где уровень значимости α – вероятность совершения ошибки первого рода.

Если F_pасч> F_{df1,df2,α ,} то полученное значение множественного коэффициента корреляции можно считать статистически значимым. В противном случае полагаем R = 0, что свидетельствует об отсутствии линейной зависимости между результирующей и факторными переменными в уравнения регрессии

В пакетах программ используется другой способ проверки гипотезы о существенности связи результирующей и факторных переменных в уравнения регрессии. Там автоматически рассчитывается p-уровень (p_F),т.е. значение вероятности, соответствующее расчетному значению F-критерия.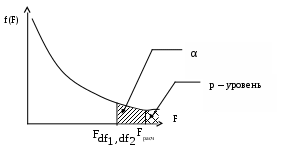



Если p_F<α, то полученное значение множественного коэффициента корреляции можно считать статистически значимым. В противном случае полагаем R = 0, что свидетельствует об отсутствии линейной зависимости между результирующей и факторными переменными в уравнения регрессии. Чем меньше значение p-уровня, тем надежнее полученные оценки.
Проверка статистической значимости коэффициентов уравнения регрессии

При таком же предположении можно проверить гипотезы относительно каждого коэффициента с использованием t-статистики Стьюдента:

a₀, a₁ – коэффициенты уравнения регрессии,

r – коэффициент корреляции.

t-статистика для коэффициента уравнения регрессии a₀ – ;

t-статистика для коэффициента уравнения регрессии a₁ – ;

t-статистика для коэффициента корреляции r – .

M_a0, m_a1, m_r – стандартные ошибки.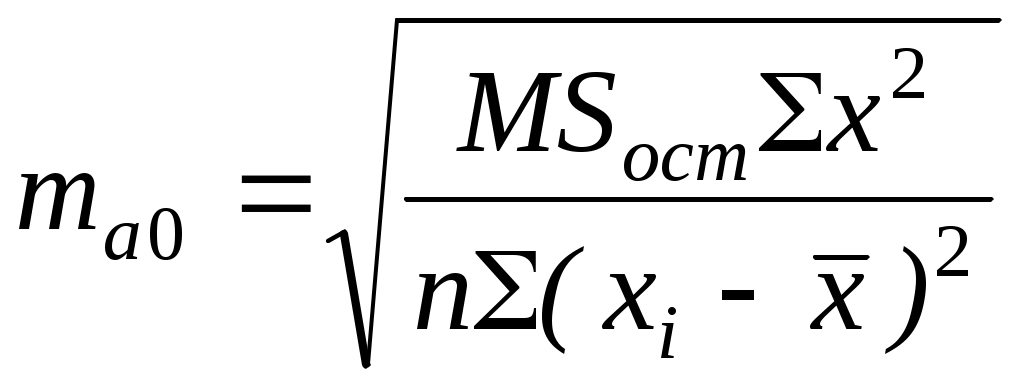

; ; .

Для проверки значимости этих коэффициентов необходимо сравнить полученные расчетные значения t_a0, t_a1, t_r с табличным значением распределения Стьюдента с df степенями свободы при уровне значимости α, т.е. с t_df,α (df = n-2).

Если расчетное значение по абсолютной величине больше табличного, то нулевая гипотеза H₀

Н₀: a₀ =0,

Н₀: a₁ = 0,

Н₀: r = 0.

отвергается и значение соответствующего коэффициента считается статистически значимым при данном уровне значимости α.

Другой способ проверки заключается в сравнении p – уровня критерия Стьюдента (p_tj) с уровнем значимости α. Если p_tj<α, то полученное значение проверяемого коэффициента уравнения регрессии можно считать статистически значимым.

Связь между F-критерием Фишера и t – статистикой Стьюдента выражается равенством:

.

Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равна проверке гипотезы о существенности связи между переменными (результирующей и факторными) в уравнении регрессии.

Качество уравнения регрессии можно также оценить с помощью средней ошибки аппроксимации




ЗАДАНИЕ:
Сгенерировать 45 значений случайной величины ε, считая, что случайная компонента ε распределена нормально с нулевым математическим ожиданием и единичной дисперсией. Для вычисления ε использовать генератор случайных чисел.
Таблица1

Номер набл.	Значение xi	Номер набл	Значение xi	Номер набл	Значение xi
1	6,5	16	9,3	31	10,4
2	10,3	17	5,7	32	10,2
3	7,7	18	12,9	33	18,0
4	15,8	19	5,1	34	13,8
5	7,4	20	3,8	35	6,0
6	14,3	21	17,1	36	11,9
7	15,4	22	8,2	37	9,4
8	21,1	23	8,1	38	13,7
9	22,1	24	11,7	39	12,0
10	12,0	25	13,0	40	11,6
11	9,5	26	15,3	41	9,1
12	8,1	27	13,5	42	6,6
13	8,4	28	10,5	43	7,6
14	15,3	29	7,3	44	9,9
15	4,3	30	13,8	45	14,7

Рассчитать 45 значений Y используя формулу

Y = 11,5 + (0,14N)x + 2ε (5)

где ε случайная компонента. Значения X возьмите из таблицы 1

Построить таблицу пар (Y,X), подставляя в уравнение (5) значения X из таблицы 1 и сгенерированные значения ε. N = Ваш номер по списку.

Используя данные таблицы (Y,X) рассчитать коэффициенты a₀ и a₁, а также коэффициент корреляции r_yx и записать уравнение регрессии.

Сделать вывод о тесноте связи используя шкалу Чеддока.

Рассчитать F – статистику Фишера и сделать вывод о статистической значимости коэффициента корреляции.
9. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ
Обобщением линейной регрессионной модели с двумя переменными является многомерная регрессионная модель (или модель множественной регрессии). Уравнение линейной регрессии 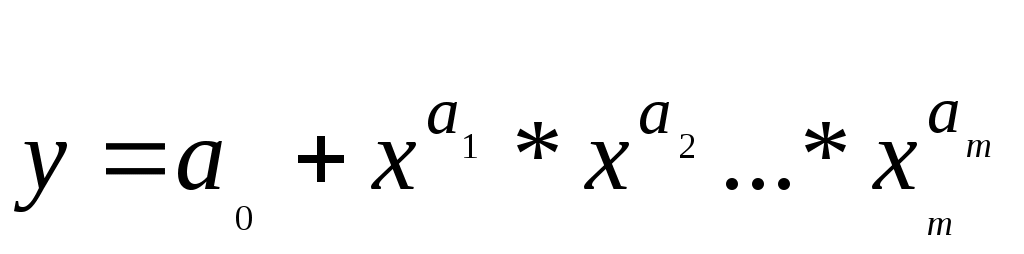. В экономике широко используется степенная функция вида: . Эта функция используется для изучения спроса и потребления, для построения производственной функции, где y – выпуск, а x – факторы производства и др.

Коэффициенты линейной модели уравнения регрессии называются коэффициентами чистой регрессии. В случае полинома коэффициенты характеризуют среднее изменение результата, при изменении соответствующего фактора на одну единицу и при неизменной величине остальных факторов.

В степенной функции коэффициенты чистой регрессии показывают, на сколько процентов изменится результат, при изменении соответствующего фактора на один процент и при фиксированном значении остальных факторов. Они играют роль коэффициентов эластичности.

Задача регрессионного анализа состоит в применении статистических методов для описания взаимосвязей между случайными величинами (признаками) с помощью математических моделей и оценки параметров этих моделей на основе данных статистического наблюдения.

Признаки разделяют на два класса: зависимые (результирующие) и независимые (факторные, предикторные, объясняющие), то есть те, от которых зависят результирующие.

Для количественной оценки зависимости между результирующими и факторными признаками определяются структура математической модели (вид аппроксимирующей функции) и ее параметры (коэффициенты аппроксимирующей функции). Оценка параметров (коэффициентов) модели производится на основе данных статистического наблюдения по совокупности показателей исследуемой зависимости. При проведении эконометрического исследования предполагается, что значения результирующей переменной носят случайный характер, поскольку зависят не только от факторных переменных, но и от тех факторов, которые мы не учитываем явно.

Обозначим: Y - зависимая переменная, а x₁, x₂,…,x_j,…,x_m – это m независимых (факторных) переменных. Здесь j – номер факторной переменной. Формально эконометрическая модель записывается следующим образом
Y = f(x₁, x₂,…,x_m) + ε. (1)

Здесь f(x₁, x₂,…,x_m) - аппроксимирующая функция m независимых переменных (детерминированная компонента), ε – случайная компонента, отражающая влияние факторов, не учтенных в модели. Уравнение вида y = f(x₁, x₂,…,x_m) называется уравнением регрессии. Частным видом эконометрической модели вида (1) является модель множественной линейной регрессии

Y = a₀ + a₁x₁ + a₂x₂ + ... + a_mx_m + ε

Коэффициенты a₁, a₂, …, a_m называются параметрами уравнения регрессии. Пусть имеется n статистических наблюдений и i – номер наблюдения. Данные статистического наблюдения можно представить в виде таблицы, состоящей из n строк вида (y_i, x_1i, x_2i,…,x_ji,…,x_mi). На основе имеющихся статистических наблюдений можно подобрать параметры a₁, a₂, …, a_m таким образом, чтобы уравнение множественной линейной регрессии наилучшим образом описывало бы наблюдаемые данные. Значения параметров a₁, a₂, …, a_m, определенные тем или иным способом называются оценками. Зная оценки параметров, модели можно использовать далее для прогнозирования значений результирующих показателей при тех или иных сочетания значений факторных показателей. Используя регрессионные модели можно проводить многовариантные расчеты по принципу «что будет, если…?». Эти модели находят широкое применение при принятии ответственных решений на практике.

Решение уравнения регрессии находится с помощью метода наименьших квадратов.

Анализ полученного решения заключается в проверке полученного уравнения регрессии путем расчета коэффициента множественной детерминации: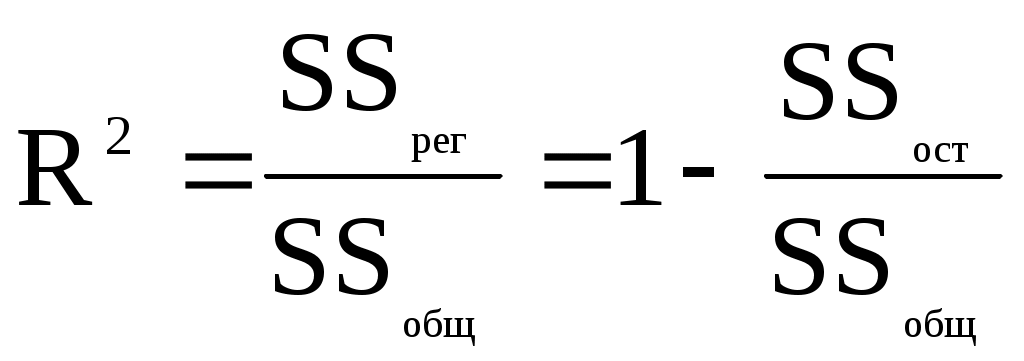



и F – статистики: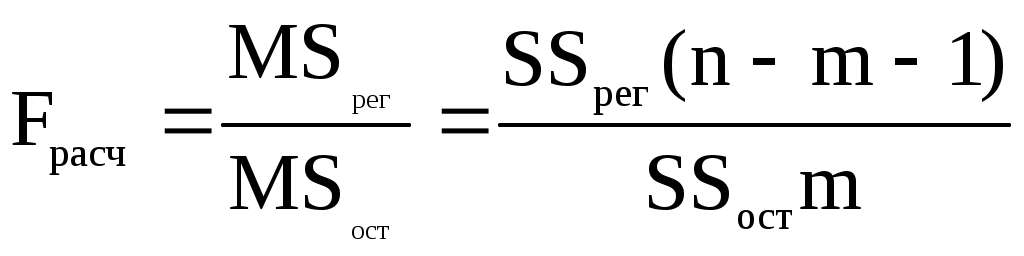

.

Если известен коэффициент детерминации R², то F – статистка может быть рассчитана следующим образом:



Рассчитанное значение сравнивается с табличным F_df1,df2,α ( ), где m – число независимых переменных, n – число наблюдений. Либо для расчетного значения F – статистики определяется p – уровень, который сравнивается с уровнем значимости α, так как это было описано в предыдущем разделе.

Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых переменных, хотя это и не обязательно означает улучшения качества регрессионной модели. Поэтому лучше пользоваться скорректированным коэффициентом детерминации, который определяется по формуле:


Проверка значимости коэффициентов регрессии аналогична проверке коэффициентов парной регрессии и сводится к вычислению значения статистики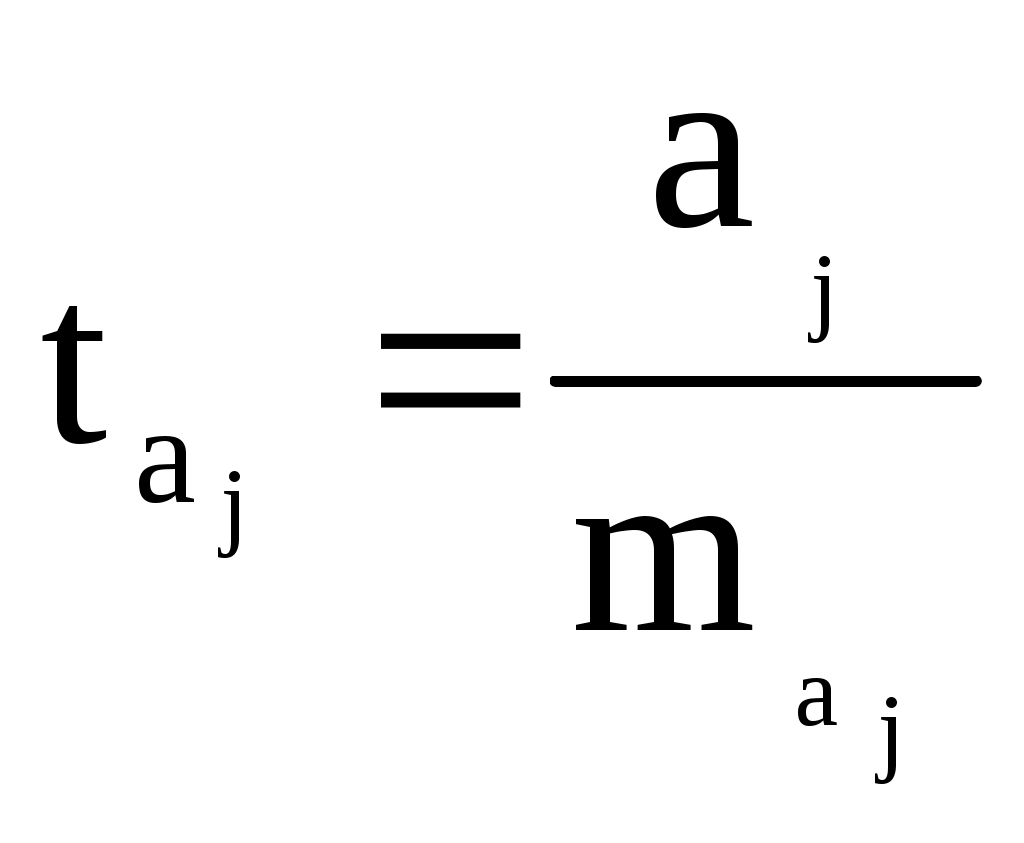

,

где - среднеквадратическая ошибка коэффициента регрессии a_j и сравнении ее с критическим значением. Альтернативой является вычисление p – уровня критерия Стьюдента (p_tj) для каждого коэффициента a_j и сравнение его с уровнем значимости α так, как это было описано выше.
Уравнение регрессии может быть преобразовано к стандартизованному масштабу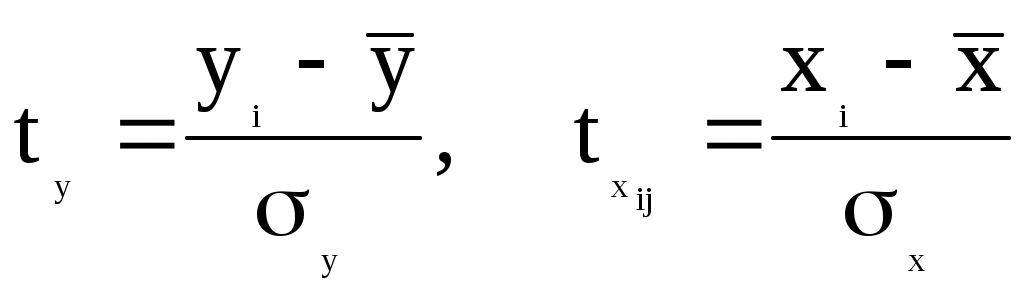

, где j – номер переменной.

Значения коэффициентов _j можно определить из уравнения: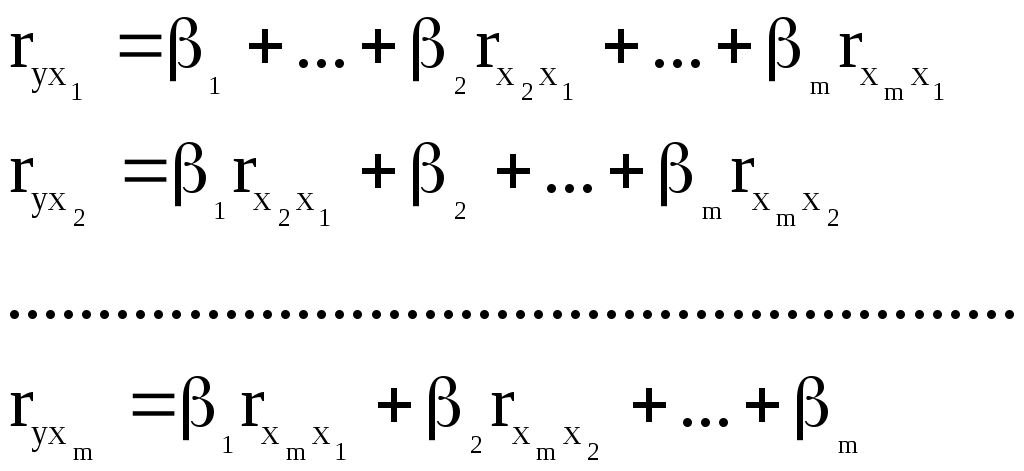

,

где - коэффициенты взаимной корреляции между x_k и x_j.

Основное достоинство стандартизованного уравнения регрессии в том, что  - коэффициенты позволяют ранжировать факторы по степени их воздействия на результат. Чем больше значение  - коэффициента, тем больший вклад вносит соответствующая факторная переменная в значение результирующей.

Коэффициенты чистой регрессии b_j связаны со стандартизованными коэффициентами _j соотношением



Решение с помощью MS Exel

С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действия следующий:

• 
  в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке OK;
  
• 
  заполните диалоговое окно ввода данных и параметров вывода. Щелкните по кнопке OK;
  

Пример использования инструмента Регрессия приведен в файле Пример.xls

Исходные данные

596	913
417	1095
354	606
526	876
934	1314
412	593
525	754
367	528
364	520
336	539
409	540
452	682
367	537
328	589
460	626
380	521
439	626
344	521
401	658
514	746
СрЗначY	СрЗначX
446,25	689,2
СтОтклY	СтОтклY
136,1179	212,9822

Две последние строки содержат выборочные средние значения и выборочные стандартные отклонения s_x, s_y, рассчитанные с помощью функции СТАНДОТКЛ.
Исходные данные вводятся в окно ввода (рис.1).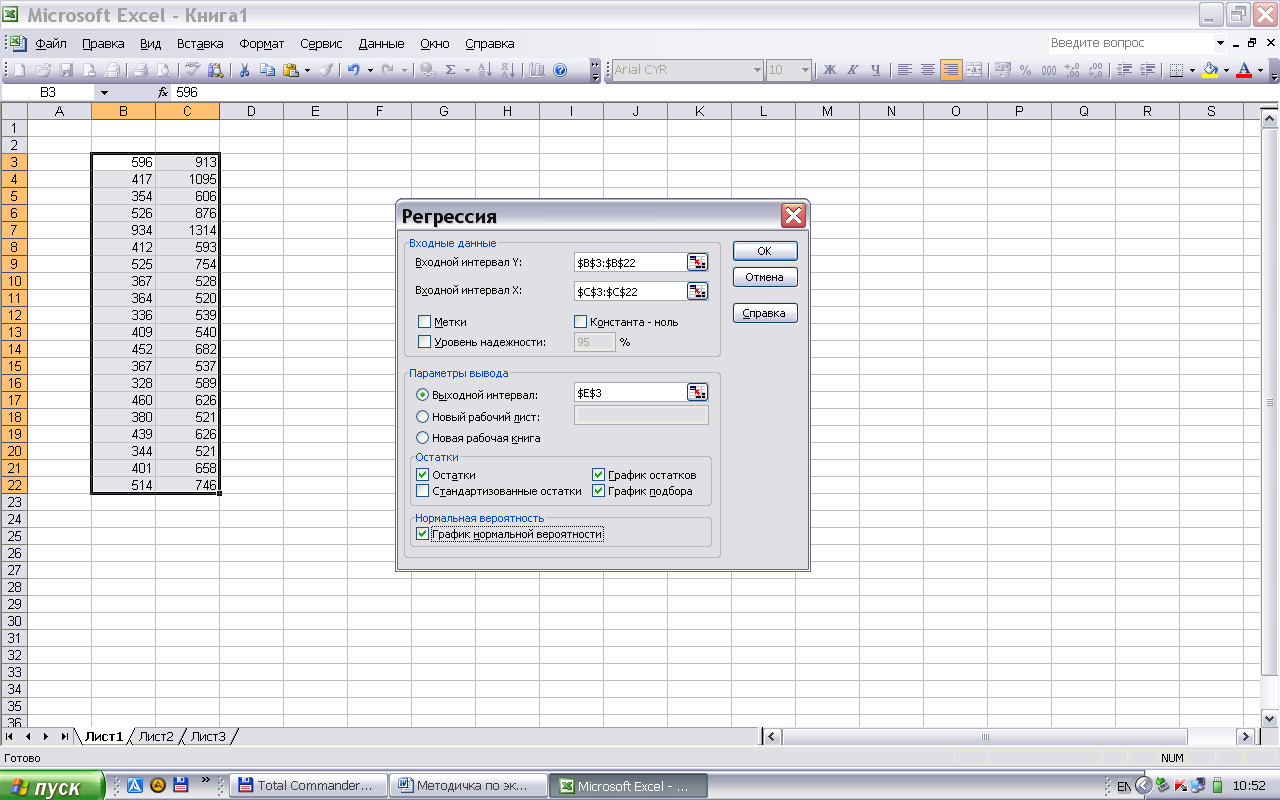



Рис 1. Окно Ввода

Результаты расчета приведены ниже. Здесь:

Множественный R - R

R-квадрат - R²

Нормированный R-квадрат -

Значимость F - p_F

Коэффициенты - значения коэффициентов (оценки)

Y-пересечение - a₀

Переменная X1 – a₁

P-Значение - p_tj

Предсказанное Y -

Остатки

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,840977
R-квадрат	0,707243
Нормированный R-квадрат	0,690979
Стандартная ошибка	75,66752
Наблюдения	20

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	248973,4	248973,4	43,48445	3,42E-06
Остаток	18	103060,3	5725,573
Итого	19	352033,8

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	75,82389	58,66674	1,292451	0,212547	-47,4303	199,0781
Переменная X 1	0,537473	0,081506	6,594274	3,42E-06	0,366235	0,70871

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
1	566,5364	29,46363
2	664,3564	-247,356
3	401,5323	-47,5323
4	546,6499	-20,6499
5	782,0629	151,9371
6	394,5451	17,45486
7	481,0782	43,92178
8	359,6094	7,390582
9	355,3096	8,690363
10	365,5216	-29,5216
11	366,0591	42,94091
12	442,3802	9,619803
13	364,4467	2,553329
14	392,3952	-64,3952
15	412,2817	47,71827
16	355,8471	24,15289
17	412,2817	26,71827
18	355,8471	-11,8471
19	429,4809	-28,4809
20	476,7784	37,22156

График подбора содержит наблюдаемые и предсказанные значения, иллюстрирует размах отклонений рассчитанных значений от наблюдаемых для переменной Y.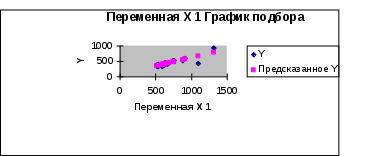

График нормального распределения используется для визуальной проверки выполнения условий Маркова-Гаусса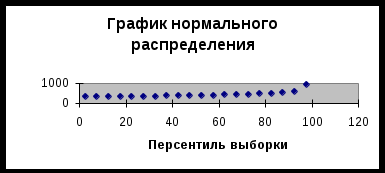