 , т.е. , т.е.
 ; ;
б) 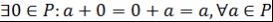 ; ;
в) 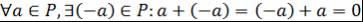 ; ;
г) коммутативность операции  , т.е. , т.е.  . .
. В  выполняются дистрибутивные законы, т.е. выполняются дистрибутивные законы, т.е.
а)  - правый дистрибутивный закон; - правый дистрибутивный закон;
б)  - левый дистрибутивный закон. - левый дистрибутивный закон.
. 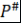 - мультипликативная абелева группа, т.е. - мультипликативная абелева группа, т.е.
а) ассоциативность операции  , т.е. , т.е.
 ; ;
б)  ; ;
в) 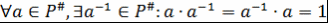 ; ;
г) коммутативность операции  , т.е. , т.е. 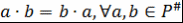 . .
Определение 16. Множество 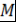 называется числовым, если называется числовым, если 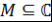 . .
Определение 17. Поле  называется числовым, если оно является числовым множеством, т.е. называется числовым, если оно является числовым множеством, т.е. 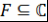 . .
Глава 2. Основы теории многочленов от одной переменной
Определение 1. Пусть  и и 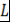 - ассоциативно-коммутативные кольца с единицами. Кольцо - ассоциативно-коммутативные кольца с единицами. Кольцо 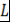 называется простым расширением кольца называется простым расширением кольца  с помощью элемента с помощью элемента 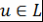 , если выполняются следующие условия: , если выполняются следующие условия:
)  - подкольцо кольца - подкольцо кольца 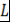 ; ;
) 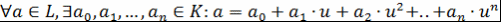 , и записывают , и записывают 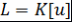 . .
Определение 2. Простое расширение  называется простым трансцендентным расширением кольца называется простым трансцендентным расширением кольца  , если выполняется следующее условие: , если выполняется следующее условие: 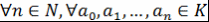 из равенства из равенства 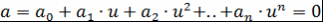 следует, что следует, что  . Элемент . Элемент 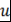 в этом случае называется трансцендентным элементом над в этом случае называется трансцендентным элементом над  (относительно (относительно  ). ).
Лемма 1. Пусть  - простое трансцендентное расширение ассоциативно-коммутативного кольца - простое трансцендентное расширение ассоциативно-коммутативного кольца  с единицей, с единицей, . Если . Если
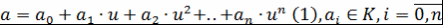 и и
 , ,
то 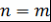 и и  . .
Лемма 2. Пусть  и и 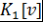 - простые трансцендентные расширения ассоциативно-коммутативных колец - простые трансцендентные расширения ассоциативно-коммутативных колец  и и  с единицами. Если с единицами. Если 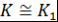 и и  - изоморфизм - изоморфизм  на на  , то , то 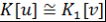 , причем существует единственный изоморфизм , причем существует единственный изоморфизм  кольца кольца  на на 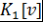 , который переводит элемент , который переводит элемент 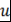 в элемент в элемент  (т.е. (т.е. 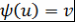 ) и продолжает изоморфизм ) и продолжает изоморфизм  . .
Следствие 2.1. Пусть 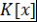 и и  - простое трансцендентное расширение ассоциативно-коммутативного кольца - простое трансцендентное расширение ассоциативно-коммутативного кольца  с единицей. Тогда с единицей. Тогда 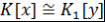 . .
Лемма 3. Пусть  - ассоциативно-коммутативное кольцо с единицей, - ассоциативно-коммутативное кольцо с единицей,  и лишь конечное число и лишь конечное число 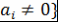 . Тогда множество . Тогда множество 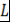 является ассоциативно-коммутативным кольцом с единицей является ассоциативно-коммутативным кольцом с единицей 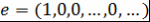 относительно операций, заданных по правилу: относительно операций, заданных по правилу:
1) 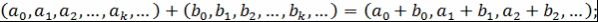
2) 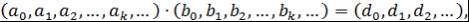 где где
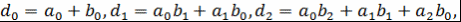 и т.д., и т.д.,
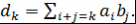
Теорема 1. Пусть  - ассоциативно-коммутативное кольцо с единицей. Тогда для - ассоциативно-коммутативное кольцо с единицей. Тогда для  существуют простые трансцендентные расширения, причём любые 2 из них изоморфны. существуют простые трансцендентные расширения, причём любые 2 из них изоморфны.
Замечание. Кольцо  , построенное в лемме 3, и являющееся простым трансцендентным расширением кольца , построенное в лемме 3, и являющееся простым трансцендентным расширением кольца  согласно теореме 1, называется кольцом многочленов (полиномов) от одной переменной (неизвестной) согласно теореме 1, называется кольцом многочленов (полиномов) от одной переменной (неизвестной)  над кольцом над кольцом  и обозначается и обозначается 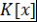 . Элементы кольца . Элементы кольца 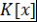 называются многочленами (полиномами) над кольцом называются многочленами (полиномами) над кольцом  от переменной от переменной 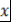 . .
Пусть, например, 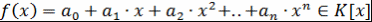 , причём , причём 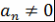 (ввиду теоремы 1). Тогда (ввиду теоремы 1). Тогда 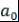 - свободный или постоянный член многочлена - свободный или постоянный член многочлена 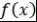 , , 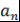 - старший коэффициент многочлена - старший коэффициент многочлена 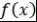 . .
Определение 3. Пусть  - ассоциативно-коммутативное кольцо с единицей, - ассоциативно-коммутативное кольцо с единицей, 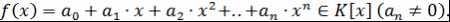 Число Число  называется степенью многочлена называется степенью многочлена  и обозначается и обозначается 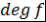 , т.е. , т.е. 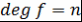 (степень многочлена - это степень переменной при старшем коэффициенте). (степень многочлена - это степень переменной при старшем коэффициенте).
Определение 4. Нулевым многочленом называется многочлен, все коэффициенты которого равны 0, и обозначается 0. По определению полагают, что степень нулевого многочлена равна  , т.е. , т.е.  . Таким образом, если . Таким образом, если  , то , то  ( (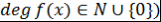 . .
Теорема 2. Пусть  - ненулевое ассоциативно-коммутативное кольцо с единицей, - ненулевое ассоциативно-коммутативное кольцо с единицей, 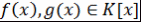 . Тогда: . Тогда:
)  ; ;
)   . .
Следствие 2.1. Пусть  - область целостности. Тогда - область целостности. Тогда  . .
Теорема 3. Если  - область целостности, то - область целостности, то 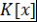 - область целостности. - область целостности.
Теорема 4. Пусть  - область целостности. Тогда для - область целостности. Тогда для 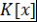 существует поле частных. существует поле частных.
Определение 5. Пусть  - ассоциативно-коммутативное кольцо с единицей. Говорят, что многочлен - ассоциативно-коммутативное кольцо с единицей. Говорят, что многочлен  делится на многочлен делится на многочлен 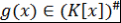 , если , если 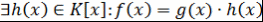 и обозначается и обозначается  или или  . .
Простейшие свойства отношения делимости в 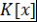 : :
1) рефлексивность 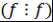 ; ; 
) транзитивность  и и  ; ;
) |
 Скачать 6.33 Mb.
Скачать 6.33 Mb.