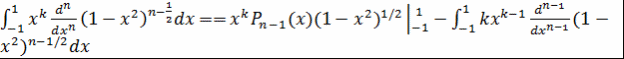Теорема 6. Многочлены Чебышева образуют ортогональную систему многочленов на отрезке 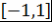 с весовой функцией с весовой функцией 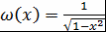 . .
Доказательство. Сделаем замену 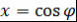 . Получим . Получим



при 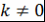 . Теорема доказана. . Теорема доказана.
Следствие 2. Если 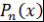 - многочлен степени - многочлен степени  и и
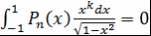
при 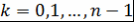 , то , то 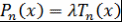 , где , где 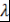 - некоторое число. - некоторое число.
Доказательство. В пространстве  со скалярным произведением со скалярным произведением

ортогональное дополнение к подпространству, порожденному многочленами 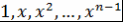 , порождено многочленом Чебышева , порождено многочленом Чебышева 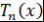 . Следствие доказано. . Следствие доказано.
Теорема 7. Многочлены Чебышева можно вычислять по формуле
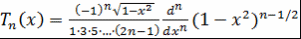 . .
Доказательство. Индукцией по  доказывается, что при доказывается, что при 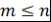  , где , где 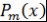 - многочлен степени - многочлен степени  , причем , причем 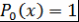 , , 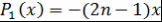 и и
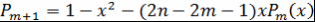 при при 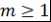 . .
Следовательно, 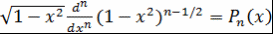 - многочлен степени - многочлен степени  . .
Проверим, что 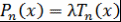 , т.е. , т.е.
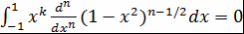
при 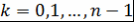 . Интегрируя по частям получаем . Интегрируя по частям получаем
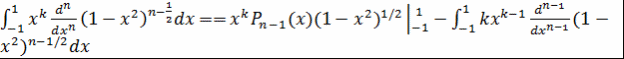
Первое слагаемое равно нулю, так как 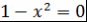 при при 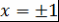 . Затем интегрируем по частям второе слагаемое и т.д. Чтобы в конце концов получить нуль, необходимо проинтегрировать по частям . Затем интегрируем по частям второе слагаемое и т.д. Чтобы в конце концов получить нуль, необходимо проинтегрировать по частям 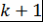 раз. При этом на последнем шаге возникнет дифференциал раз. При этом на последнем шаге возникнет дифференциал  . Это означает, что число . Это означает, что число 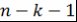 должно быть неотрицательно, т.е. должно быть неотрицательно, т.е.  . .
Остается проверить, что 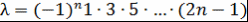 . Для этого вычисляют . Для этого вычисляют 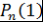 . Действительно, что при . Действительно, что при  рекуррентное соотношение рекуррентное соотношение 
принимает вид  . Таким образом, . Таким образом,
 . Кроме того, . Кроме того, 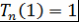 . Теорема доказана. . Теорема доказана.
Теорема 8. Пусть многочлен 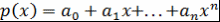 , где , где 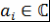 , таков, что , таков, что 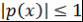 при при 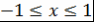 . Тогда . Тогда 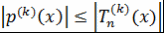 при при 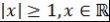 . .
Доказательство. Воспользуемся тем, что 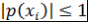 при при 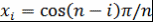 , , 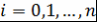 . Многочлен . Многочлен  полностью определяется значениями полностью определяется значениями  . .
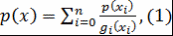
Где

Дифференцируя 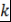 раз соотношение (1), получим раз соотношение (1), получим

Так как 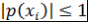 , то , то

Многочлен 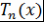 в точке в точке 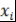 принимает значение принимает значение 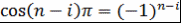 . Поэтому . Поэтому
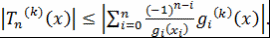
Кроме того,  . Далее, при . Далее, при  знак числа знак числа 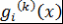 не зависит от не зависит от 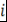 . Действительно, все корни многочлена . Действительно, все корни многочлена 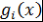 принадлежат отрезку принадлежат отрезку 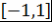 . Поэтому все корни многочлена . Поэтому все корни многочлена 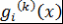 также принадлежат этому отрезку. Следовательно, также принадлежат этому отрезку. Следовательно, 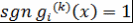 при при 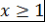 и и 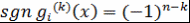 при при 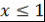 . .
В итоге при  получаем получаем

В этом случае из неравенства (2) следует, что 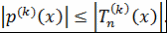 Теорема доказана. Теорема доказана.
Теорема 9. Пусть многочлен 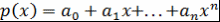 , где , где 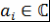 , таков, что , таков, что 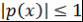 при при 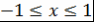 . Тогда . Тогда 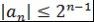 . .
Доказательство. Так как  , где , где 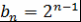 , то по теореме 8 при , то по теореме 8 при 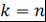 получим получим 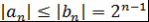 . Теорема доказана. . Теорема доказана.
Теорема 10. При 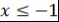 и при и при 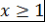 выполняется неравенство выполняется неравенство 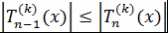 . .
Доказательство. Для многочлена  выполняется условие теоремы 8. Поэтому выполняется условие теоремы 8. Поэтому 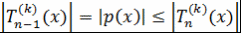 . Теорема доказана. . Теорема доказана.
Теорема 11. При 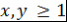 выполняется неравенство выполняется неравенство
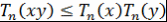 . .
Доказательство. Пусть  . Рассмотрим многочлен . Рассмотрим многочлен 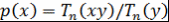 . Проверим, что многочлен . Проверим, что многочлен  удовлетворяет условию теоремы 8, т.е. что удовлетворяет условию теоремы 8, т.е. что 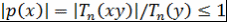 при при 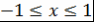 . При вещественном . При вещественном 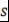 функция функция 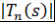 зависит только от зависит только от 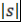 , причем если , причем если 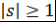 , то , то 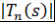 монотонно возрастает с возрастанием монотонно возрастает с возрастанием 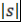 . Кроме того, . Кроме того,
 при при 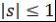 . Следовательно, если . Следовательно, если 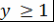 и и 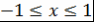 , то , то  . .
Согласно теореме 8 при 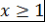 выполняется неравенство выполняется неравенство  , т.е. , т.е. 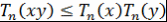 . Теорема доказана. . Теорема доказана.
Определение 6. Для последовательности функций 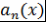 рассматривают ряд рассматривают ряд 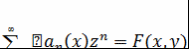 . Если радиус сходимости данного ряда положителен, то функцию . Если радиус сходимости данного ряда положителен, то функцию 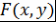 называют производящей функцией последовательности называют производящей функцией последовательности 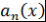 . .
Теорема 12. При 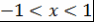 и и 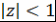 выполняются следующие равенства: выполняются следующие равенства:
(а) 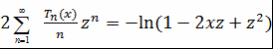
(б)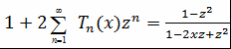 . .
Доказательство.
а) Пусть |
 Скачать 6.33 Mb.
Скачать 6.33 Mb.