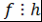 и и  ; ;
)  ; ;
) . .
Определение 6. Пусть  - ассоциативно-коммутативное кольцо с единицей, - ассоциативно-коммутативное кольцо с единицей, 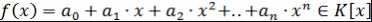 (т.е. (т.е.  ), ),  . Элемент . Элемент  называется значением многочлена называется значением многочлена 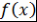 в точке в точке 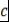 (на элементе (на элементе 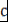 ) и обозначается ) и обозначается  , то есть , то есть 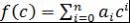 . .
Теорема 5 (теорема Безу). Пусть  - ассоциативно-коммутативное кольцо с единицей, - ассоциативно-коммутативное кольцо с единицей, 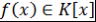 , ,  . Тогда существует . Тогда существует  такой, что такой, что 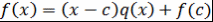 . .
Доказательство. Пусть  . Тогда . Тогда  . .
Таким образом, 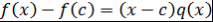 , где , где  . Теорема доказана. . Теорема доказана.
Определение 7. Пусть  - ассоциативно-коммутативное кольцо с единицей, - ассоциативно-коммутативное кольцо с единицей, 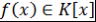 . Элемент . Элемент  называется корнем многочлена называется корнем многочлена 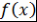 , если , если 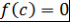 . .
Следствие 5.1. Пусть  - ассоциативно-коммутативное кольцо с единицей, - ассоциативно-коммутативное кольцо с единицей, 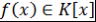 , ,  . Тогда . Тогда 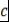 - корень - корень  делится на делится на 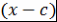 . .
Следствие 5.2. При делении многочлена 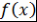 на на 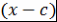 получается остаток получается остаток  , равный , равный 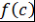 . .
Теорема 6. Пусть  - область целостности, - область целостности, 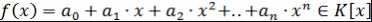 , , 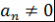 . Тогда многочлен . Тогда многочлен 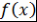 имеет не более имеет не более  попарно различных корней. Другими словами, любой ненулевой многочлен -й степени над областью целостности имеет не более попарно различных корней. Другими словами, любой ненулевой многочлен -й степени над областью целостности имеет не более  попарно различных корней. попарно различных корней.
Доказательство. Доказательство проведём методом математической индукции по параметру  . .
) Пусть 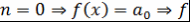 не имеет корней, т.е. не имеет корней, т.е.  имеет нуль корней и значит имеет нуль корней и значит  - верно. - верно.
) Пусть  . Предположим, что утверждение верно при . Предположим, что утверждение верно при  . .
) Докажем, что утверждение верно при 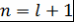 : : 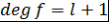 . Если . Если  не имеет корней, то число корней равно не имеет корней, то число корней равно 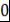 и и  - верно. Пусть - верно. Пусть  имеет хотя бы один корень и имеет хотя бы один корень и 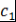 - корень - корень 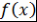 такой, что такой, что 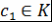 . Тогда по теореме Безу . Тогда по теореме Безу  , где , где  , причём , причём 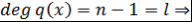 по пункту 2) по пункту 2) 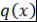 имеет не более имеет не более 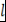 попарно различных корней. попарно различных корней.
Покажем, что все корни многочлена 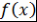 , отличные от , отличные от 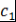 , являются также корнями многочлена , являются также корнями многочлена 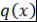 . Пусть . Пусть  - корень - корень 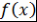 , , 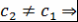
 , т.е. , т.е.  так как так как  - область целостности) - область целостности)   - корень - корень 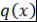 . Таким образом, многочлен . Таким образом, многочлен 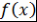 имеет корень имеет корень 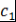 , а все остальные корни многочлена , а все остальные корни многочлена  являются также корнями многочлена являются также корнями многочлена 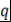 . Так как . Так как 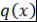 имеет не более имеет не более 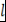 попарно различных корней, то многочлен попарно различных корней, то многочлен  имеет не более, чем имеет не более, чем  попарно различных корней. попарно различных корней.
Из 1)-3) по методу математической индукции следует, что утверждение верно для любого 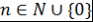 . Теорема доказана. . Теорема доказана.
Следствие 6.1. Пусть  - область целостности, - область целостности,  . Если многочлен . Если многочлен 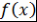 имеет более имеет более  попарно различных корней, то попарно различных корней, то 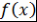 является нулевым многочленом. является нулевым многочленом.
Определение 8. Пусть 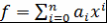 , ,  , где , где  - ассоциативно-коммутативное кольцо с единицей. Многочлены - ассоциативно-коммутативное кольцо с единицей. Многочлены  и и  называются алгебраически равными, если называются алгебраически равными, если 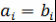 , ,  . .
Определение 9. Многочлены  и и  из из 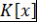 называются функционально равными, если называются функционально равными, если 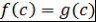 , , 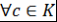 , т.е. значения многочленов , т.е. значения многочленов  и и  в любой точке кольца в любой точке кольца  совпадают. совпадают.
Теорема 7. Пусть  - бесконечная область целостности, - бесконечная область целостности, . Многочлены . Многочлены  и и  алгебраически равны алгебраически равны  и и  равны функционально. равны функционально.
Теорема 8. Пусть 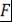 - поле, - поле,  . Тогда существуют единственные многочлены . Тогда существуют единственные многочлены  такие, что такие, что 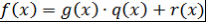 , причем , причем  . .
Определение 10. Пусть 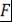 - поле, - поле,  . Многочлен . Многочлен 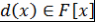 называется наибольшим общим делителем многочленов называется наибольшим общим делителем многочленов 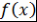 и и 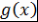 (или коротко, НОД (или коротко, НОД 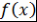 и и 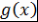 ) и обозначается ) и обозначается  , если выполняются два условия: , если выполняются два условия:
) 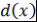 - общий делитель многочленов - общий делитель многочленов 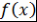 и и 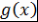 , т.е. , т.е.  и и 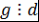 ; ;
) 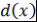 делится на любой общий делитель многочленов делится на любой общий делитель многочленов 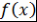 и и 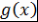 , т.е. если , т.е. если  и и 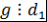 , то , то |
 Скачать 6.33 Mb.
Скачать 6.33 Mb. .
. . Теорема доказана.
. Теорема доказана.