 . Пусть, например, . Пусть, например,  . Так как левая часть . Так как левая часть  делится на делится на  , то , то 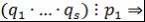 по лемме 4 хотя бы один из множителей делится на по лемме 4 хотя бы один из множителей делится на  . Так как множители можем менять местами, то будем считать, что . Так как множители можем менять местами, то будем считать, что 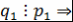 по лемме 8 по лемме 8 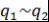 и по замечанию 3 и по замечанию 3  , где , где 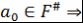  , , 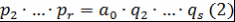 . Так как левая часть . Так как левая часть 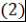 делится на делится на  , то, как и выше, получим , то, как и выше, получим  и и 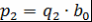 , где , где 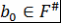 , причем , причем 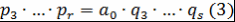 и т.д., через конечное число шагов получим и т.д., через конечное число шагов получим 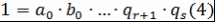 . Допустим, что . Допустим, что  противоречие противоречие  . Таким образом, представление многочлена . Таким образом, представление многочлена 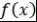 в виде требуемого произведения определяется однозначно с точностью до порядка следования множителей и ассоциированности. Теорема доказана. в виде требуемого произведения определяется однозначно с точностью до порядка следования множителей и ассоциированности. Теорема доказана.
Определение 15. Пусть  - поле. Многочлен - поле. Многочлен  называется нормированным или приведенным, если называется нормированным или приведенным, если 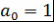 . .
Следствие 10.1. Любой многочлен  положительной степени над полем положительной степени над полем  допускает представление в виде: допускает представление в виде: 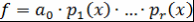 , где , где 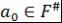 , , 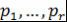 - неприводимые над - неприводимые над  нормированные многочлены. нормированные многочлены.
Определение 16. Пусть 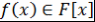 , ,  - поле, - поле, 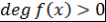 . Представление многочлена . Представление многочлена 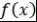 в виде в виде 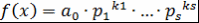 , где , где 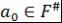 , ,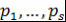 - попарно различные неприводимые над полем - попарно различные неприводимые над полем  нормированные многочлены, нормированные многочлены, 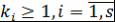 , называется каноническим представлением многочлена , называется каноническим представлением многочлена  , число , число  называется кратностью множителя называется кратностью множителя 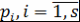 . Если . Если  , то , то 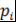 называется простым неприводимым множителем многочлена называется простым неприводимым множителем многочлена  . .
Определение 17. Пусть 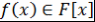 , ,  - ассоциативно-коммутативное кольцо с единицей, - ассоциативно-коммутативное кольцо с единицей, 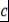 - корень - корень 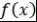 . Число . Число 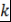 называется кратностью корня называется кратностью корня 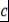 многочлена многочлена 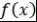 , если , если  , но , но 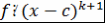 . .
В этом случае пишут 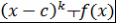 - данная запись означает, что - данная запись означает, что 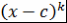 - это наибольшая степень - это наибольшая степень  , которая делит , которая делит 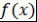 . .
Теорема 11. Пусть  - несократимая рациональная дробь. Если - несократимая рациональная дробь. Если  - корень - корень 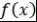 , то , то  . .
Доказательство. Так как 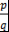 - корень - корень 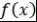 , то , то 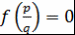 , то есть: , то есть:

 . Так как . Так как 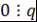 , то , то  . Так как . Так как 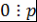 , то , то 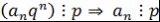 . .
Теорема доказана.
Следствие 11.1. Рациональные корни нормированного многочлена с целыми коэффициентами являются его целыми корнями.
Следствие 11.2. Целые корни многочлена с целыми коэффициентами являются делителями свободного числа.
Теорема 12. Пусть 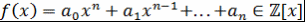 , , 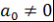 , , 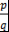 - несократимая рациональная дробь. Если - несократимая рациональная дробь. Если 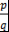 - корень - корень 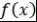 , то , то 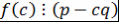 , , 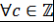 . .
Следствие 12.1. Пусть  , , 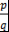 - несократимая рациональная дробь. Если - несократимая рациональная дробь. Если 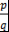 - корень - корень 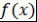 , то , то  , ,  . .
Глава 3. Многочлены Чебышева и их основные свойства
3.1 Определение и простейшие свойства многочленов Чебышева
многочлен чебышев корень переменная
Определение 1. Многочлены 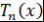 , где , где  , определенные рекуррентным соотношением , определенные рекуррентным соотношением  и начальными условиями и начальными условиями 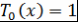 и и  называют многочленами Чебышева. называют многочленами Чебышева.
Определение многочленов Чебышева основано на том, что  полиномиально выражается через полиномиально выражается через 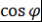 , т.е. существует такой многочлен , т.е. существует такой многочлен 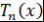 , что , что  при при 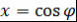 . .
Формула 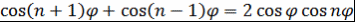 показывает, что многочлены показывает, что многочлены 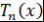 , определенные рекуррентным соотношением , определенные рекуррентным соотношением  и начальными условиями и начальными условиями 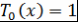 и и  , обладают нужным свойством. , обладают нужным свойством.
Непосредственно из того, что  при при 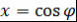 , следует, что , следует, что  при при 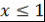 . А из рекуррентного соотношения следует, что . А из рекуррентного соотношения следует, что 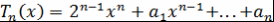 , где , где 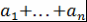 - целые числа. - целые числа.
Теорема 1. Пусть 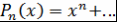 - многочлен степени - многочлен степени  со старшим коэффициентом 1, причем со старшим коэффициентом 1, причем 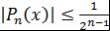 при при  . .
Тогда 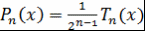 . Другими словами, многочлен . Другими словами, многочлен 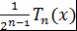 - наименее уклоняющийся от нуля на интервале - наименее уклоняющийся от нуля на интервале 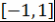 многочлен степени многочлен степени  со старшим коэффициентом 1. со старшим коэффициентом 1.
Доказательство. Воспользуемся свойством многочлена 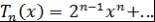 , а именно тем, что , а именно тем, что 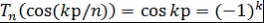 при при  . Рассмотрим многочлен . Рассмотрим многочлен 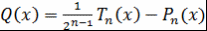 . Его степень не превосходит . Его степень не превосходит 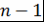 , поскольку старшие члены многочленов , поскольку старшие члены многочленов 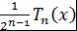 и и  равны. Из того, что равны. Из того, что 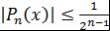 при при  , следует, что в точке , следует, что в точке
 знак числа знак числа 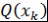 cовпадает со знаком числа cовпадает со знаком числа  . Таким образом, в концах каждого отрезка . Таким образом, в концах каждого отрезка 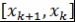 многочлен многочлен 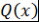 принимает значения разного знака. Поэтому у многочлена принимает значения разного знака. Поэтому у многочлена 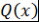 на этом отрезке есть корень. В случае, когда на этом отрезке есть корень. В случае, когда 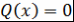 , либо , либо |
 Скачать 6.33 Mb.
Скачать 6.33 Mb.