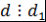 . .
Лемма 4. Пусть  - поле, - поле, 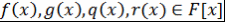 , , 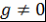 и и 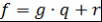 . Тогда НОД многочленов . Тогда НОД многочленов  и и  и НОД многочленов и НОД многочленов  и и  ассоциированы, т.е. ассоциированы, т.е. 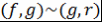 . .
Лемма 5. НОД двух многочленов определяется однозначно с точностью до ассоциированности.
Определение 11. Пусть  - поле, - поле,  . Многочлен . Многочлен 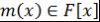 называется наименьшим общим кратным многочленов называется наименьшим общим кратным многочленов 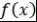 и и 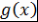 (или коротко, НОК (или коротко, НОК 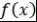 и и 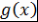 ) и обозначается ) и обозначается 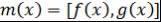 , если выполняются два условия: , если выполняются два условия:
) 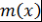 - общее кратное многочленов - общее кратное многочленов 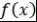 и и 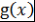 , т.е. , т.е. 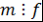 и и 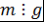 ; ;
) 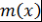 делит любое общее кратное многочленов делит любое общее кратное многочленов 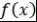 и и 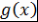 , т.е. если , т.е. если 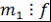 и и 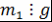 , то , то 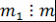 . .
Лемма 6. НОК двух многочленов определяется однозначно с точностью до ассоциированности.
Пусть  - поле, - поле,  . Для нахождения НОК многочленов . Для нахождения НОК многочленов 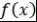 и и 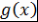 применяется следующая формула: применяется следующая формула: 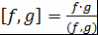 . .
Теорема 9 (теорема о линейном представлении НОД). Пусть  - поле, - поле,  , , 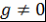 , , 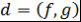 . Тогда . Тогда 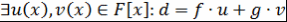 . .
Определение 12. Пусть  - поле, - поле,  , ,  . Многочлен вида . Многочлен вида 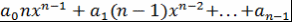 называется формальной производной многочлена называется формальной производной многочлена 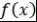 и обозначается и обозначается 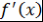 . .
Нетрудно проверить, что формальная производная многочлена удовлетворяет следующим свойствам:
) 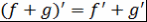 ; ;
) 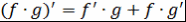 ; ;
) 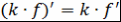 ; ;
) 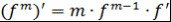 . .
Определение 13. Многочлен 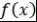 положительной степени над полем положительной степени над полем  называется неприводимым над называется неприводимым над , если он не допускает представления в виде произведения двух многочленов над полем , если он не допускает представления в виде произведения двух многочленов над полем  меньшей степени. меньшей степени.
Определение 14. Многочлен 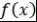 положительной степени над полем положительной степени над полем  называется приводимым над называется приводимым над  , если он допускает представление в виде произведения двух многочленов над полем , если он допускает представление в виде произведения двух многочленов над полем  меньшей степени. меньшей степени.
Лемма 7. Многочлен первой степени неприводим над любым полем.
Лемма 8. Пусть  - поле, - поле, 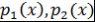 - неприводимые над - неприводимые над  многочлены. Если многочлены. Если 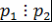 , то , то 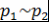 . .
Замечание 1. Пусть  - поле. Тогда - поле. Тогда  - область целостности - область целостности 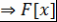 - область целостности - область целостности 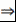 все элементы области целостности все элементы области целостности 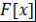 подразделяются на 4 вида: подразделяются на 4 вида:
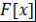 = =       
Замечание 2. Поскольку НОД и НОК многочленов определяются однозначно с точностью до ассоциированности, то многочлены  и и  являются взаимно простыми являются взаимно простыми 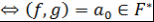 . .
Замечание 3. Пусть  - неприводимый над - неприводимый над  многочлен. Если многочлен. Если 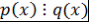 , то либо , то либо 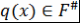 , либо , либо 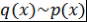 . .
Лемма 9. Пусть  - поле, - поле, 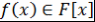 , ,  - неприводимый над - неприводимый над  многочлен. f многочлен. f  p p 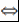  и и  взаимно просты. взаимно просты.
Лемма 10. Пусть  - поле, - поле, 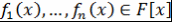 , ,  - неприводимый над - неприводимый над  многочлен. Если многочлен. Если 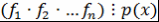 , то хотя бы , то хотя бы 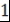 из множителей из множителей  делится на делится на  , то есть , то есть 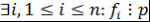 . .
Теорема 10. (Основная теорема о многочленах). Любой многочлен положительной степени над полем  допускает представление в виде произведения неприводимых над допускает представление в виде произведения неприводимых над  многочленов, причем такое представление единственно с точностью до порядка следования множителей и ассоциированности. многочленов, причем такое представление единственно с точностью до порядка следования множителей и ассоциированности.
Доказательство. 1) Существование. Пусть 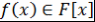 и и 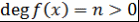 . Доказательство проведем методом математической индукции по параметру . Доказательство проведем методом математической индукции по параметру  . .
. Пусть 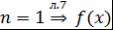 неприводим над неприводим над 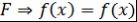 - искомое представление. - искомое представление.
. Допустим, что утверждение верно для любого многочлена положительной степени 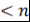 над полем над полем  . .
. Докажем утверждение для многочлена 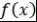 . Если . Если 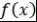 неприводим над неприводим над  , то , то  - искомое представление. Пусть - искомое представление. Пусть 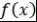 приводим над приводим над 
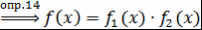 , где , где 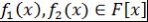 и и 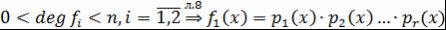 и и 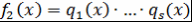 - представление - представление 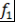 и и 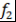 в виде произведения неприводимых над в виде произведения неприводимых над  многочленов многочленов  - искомое представление. - искомое представление.
Из 1-3 по методу математической индукции 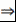 утверждение верно для любого утверждение верно для любого 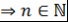 . .
) Единственность. Пусть 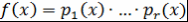 и и 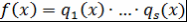 - требуемые представления - требуемые представления 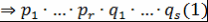 . Так как . Так как 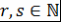 , то либо , то либо 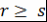 , либо , либо |
 Скачать 6.33 Mb.
Скачать 6.33 Mb.



