Многочлены Чебышева и их основные свойства
 Скачать 6.33 Mb.
|
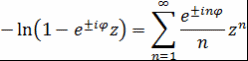 . Тогда  . Поэтому  . Кроме того, при  . Следовательно, Теорема доказана. б) Продифференцировав по  обе части равенства (а), получим Следовательно,  Теорема доказана. Теорема 13. Пусть  и  . Тогда Доказательство. Согласно теореме 12 (а),   Поэтому  Суммирование ведется до тех пор, пока  . Поэтому  . Теорема доказана.Для многочлена  : где  При  выполняется равенство а при  выполняется равенство Таким образом, если  , а при многочлены  задаются формулой (1), то выполняется соотношение где Соотношения (1) и (2) можно записать следующим образом. Пусть 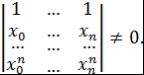 и  , где  - некоторое фиксированное число. Тогда (при  второе соотношение принимает вид  ). Покажем, что соотношения (3) эквивалентны не только для указанных последовательностей, но и для произвольных последовательностей. Заметим, что первое соотношение имеет вид  , а второе соотношение имеет вид  . Поэтому каждое соотношение однозначно определяет как последовательность  по последовательности  , так и последовательность по последовательности . Для последовательностей  ,  , где  и  - фиксированные наборы чисел, соотношения (3) эквивалентны, поскольку они эквивалентны для последовательностей  ,  . Проверим, что для любой последовательности  можно подобрать такие числа  и  , что при  . Выберем произвольные попарно различные числа . Тогда для чисел получим систему линейных уравнений с определителем Эта система уравнений имеет решение при любых  .Соотношение (3) позволяют получать нетривиальные тождества с биномиальными коэффициентами. Пусть, например,  при всех  . Тогда  Данные тождества получаются из разложений  и  по биному Ньютона. В таком случае соотношение  принимает вид   Заключение В курсовой работе ¾ изучены основные понятия теории многочленов от одной переменной (многочлен, степень многочлена, нулевой многочлен, неприводимый (приводимый) над полем многочлен, наибольший общий делитель и наименьшее общее кратное многочленов над полем, каноническое представление многочлена, корень многочлена, кратность корня многочлена и др.), приведены примеры многочленов (многочлены над числовыми полями), рассмотрены основные свойства многочленов от одной переменной (свойства кольца многочленов над областью целостности, свойства степени многочлена, свойства неприводимых многочленов над полем и др.); ¾ изучены и детально изложены центральные результаты о многочленах Чебышева: теорема Чебышева о наименее уклоняющемся от нуля на интервале [-1,1] нормированном многочлене, теоремы о вычислении значений многочлена Чебышева, теорема о свойстве коммутирования многочленов Чебышева, теорема об эквивалентных парах многочленов, теорема об ортогональности системы многочленов Чебышева, теоремы о неравенствах для многочленов Чебышева). Список используемой литературы 1. Прасолов В.В. Многочлены. - М.: МЦНМО, 2001. 2. Винберг Э.Б. Курс алгебры. - М.: МЦНМО, 2011. . Куликов Л.Я. Алгебра и теория чисел. - М.: Оникс, 2012. . Кострикин А.И. Введение в алгебру. В 3-х частях. Часть 1: Основы алгебры: учебник. - М.: МЦНМО, 2009. . Кострикин А.И. Введение в алгебру. В 3-х частях. Часть 2: Линейная алгебра: учебник. - М.: МЦНМО, 2012. . Кострикин А.И. Введение в алгебру. В 3-х частях. Часть 3: Основные структуры алгебры: учебник. - М.: МЦНМО, 2009. . Курош А.Г. Основы высшей алгебры. - СПб.: Лань, 2011. . Курош А.Г. Лекции по общей алгебре. - СПб.: Лань, 2007. . Родина М.А., Солодовников А. С. Задачник-практикум по алгебре. - М.: Просвещение, 1986. . Фаддеев Д.К. Лекции по алгебре. - СПб.: Лань, 2007. . Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. - СПб.: Лань, 2008. . Окунев Л.Я. Высшая алгебра. - СПб.: Лань, 2009. . Прасолов В.В., Шварцман О.В. Азбука римановых поверхностей. - М.: Фазис, 1999. |