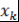 - двукратный корень, либо внутри одного из отрезков - двукратный корень, либо внутри одного из отрезков 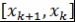 и и  есть еще один корень. Это следует из того, что в точках есть еще один корень. Это следует из того, что в точках 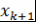 и и  мнгочлен мнгочлен 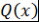 принимает значения одного знака (рис.1). принимает значения одного знака (рис.1).

Рис.1
Количество отрезков 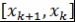 равно равно  , поэтому многочлен , поэтому многочлен 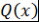 имеет по крайней мере имеет по крайней мере  корней. Для многочлена степени не более корней. Для многочлена степени не более 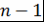 это означает, что он тождественно равен нулю, т.е. это означает, что он тождественно равен нулю, т.е. 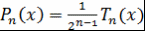 . Теорема доказана. . Теорема доказана.
Теорема 2. Пусть 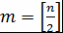 . Тогда . Тогда
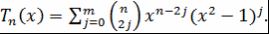
Доказательство. Поскольку  , то , то 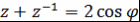 и и  . Следовательно, . Следовательно,  . .
Пусть 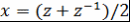 и и 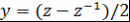 . Тогда . Тогда 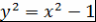 и и

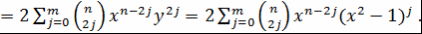
Теорема доказана.
Следствие 1. Пусть  - нечетное простое число. Тогда - нечетное простое число. Тогда
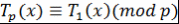 . .
Доказательство. Запишем  в виде в виде 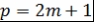 . Тогда . Тогда
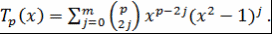
Если 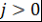 , то , то  делится на делится на  . Поэтому . Поэтому
 . Следствие доказано. . Следствие доказано.
Определение 2. Композиция многочленов  и и  определяется равенством определяется равенством  . .
Определение 3. Многочлены  и и  называются коммутирующими, если называются коммутирующими, если 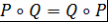 , т.е. , т.е.  . .
Теорема 3. Многочлены 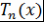 и и 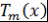 коммутирующие. коммутирующие.
Доказательство. Пусть 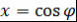 . Тогда . Тогда  и и 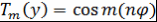 . Поэтому . Поэтому 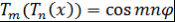 . Аналогично . Аналогично 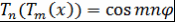 . Таким образом, равенство . Таким образом, равенство 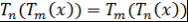 выполняется при выполняется при 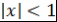 , а значит, это равенство выполняется при всех , а значит, это равенство выполняется при всех 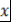 . Теорема доказана. . Теорема доказана.
Определение 4. Пусть 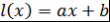 , где , где 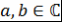 и и  . Говорят, что пара многочленов . Говорят, что пара многочленов 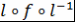 и и  эквивалентна паре многочленов эквивалентна паре многочленов 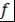 и и  . .
Теорема 4 (Ритт). Пусть и и  - коммутирующие многочлены. Тогда пара многочленов - коммутирующие многочлены. Тогда пара многочленов 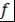 и и  эквивалентна одной из следующих пар: эквивалентна одной из следующих пар:
(1) 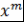 и и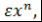 где где
(2) 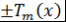 и и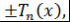 где где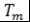 и и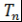 - многочлены Чебышева; - многочлены Чебышева;
(3) 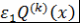 и и где где
Теорема 4 была доказана в 1922 году американским математиком Риттом; все известные ее доказательства весьма сложные. Современное изложение доказательства теоремы Ритта приведено в книге Прасолова В.В., Шварцмана О.В. [13].
В некоторых случаях вместо многочлена 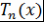 рассматривают многочлен рассматривают многочлен 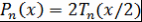 со старшим коэффициентом 1. Многочлены со старшим коэффициентом 1. Многочлены 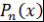 удовлетворяют рекуррентному соотношению удовлетворяют рекуррентному соотношению 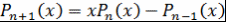 . Поэтому . Поэтому 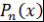 - многочлен с целыми коэффициентами. - многочлен с целыми коэффициентами.
Если 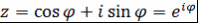 , то , то 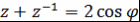 и и  . Следовательно, . Следовательно, 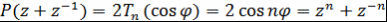 , т.е. многочлен , т.е. многочлен 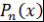 соответствует полиномиальному выражению величины соответствует полиномиальному выражению величины 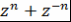 через через 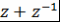 . .
С помощью многочленов 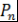 можно доказать следующее утверждение. можно доказать следующее утверждение.
Теорема 5. Если оба числа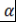 и и 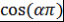 рациональны, то число рациональны, то число 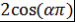 целое, т.е. целое, т.е. . .
Доказательство. Пусть 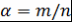 - несократимая дробь и - несократимая дробь и 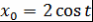 , где , где 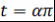 . Тогда . Тогда  . Поэтому . Поэтому 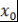 - корень многочлена - корень многочлена  с целыми коэффициентами. Пусть с целыми коэффициентами. Пусть 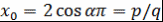 - несократимая дробь. Тогда - несократимая дробь. Тогда 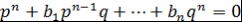 , и значит, , и значит, 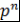 делится на делится на 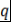 . Однако числа . Однако числа 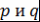 взаимно простые. Поэтому взаимно простые. Поэтому 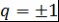 , т.е. , т.е.  - целое число. Теорема доказана. - целое число. Теорема доказана.
3.2 Основные теоремы о многочленах Чебышева
Определение 5. Многочлены 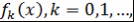 называют ортогональными многочленами на отрезке называют ортогональными многочленами на отрезке 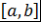 с весовой функцией с весовой функцией 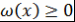 , если , если 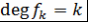 и и  при при 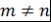 . .
В пространстве  многочленов степени не более многочленов степени не более  задают скалярное произведение формулой задают скалярное произведение формулой  . .
Ортогональные многочлены 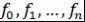 образуют ортогональный базис в пространстве образуют ортогональный базис в пространстве  с таким скалярным произведением. с таким скалярным произведением.
Если задан отрезок и весовая функция, то ортогональные многочлены определены однозначно с точность до пропорциональности. В самом деле, они получаются в результате ортогонализации базиса 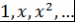
Наиболее известны следующие ортогональные многочлены:
|

|
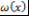
|
Название
|
-1
|
1
|
1
|
многочлены Лежандра
|
-1
|
1
|

|
многочлены Гегенбауэра
|
-1
|
1
|
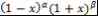
|
многочлены Якоби
|

|

|

|
многочлены Эрмита
|
0
|

|
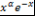
|
многочлены Лагерра
| |
 Скачать 6.33 Mb.
Скачать 6.33 Mb.
