Лекция № 1, математика Множества. Множества и операции над ними

• Название: Множества и операции над ними
• Дата: 02.03.2023
• Размер: 0.62 Mb.
• Имя файла: Лекция № 1, математика Множества.doc
• Тип: Лекция; #964262
• страница: 3 из 4

8. Вычитание множеств. Дополнение множества

Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.

Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.

Разность множеств А и В обозначают А \ В. Тогда, по определению, имеем: А\В={х |х А и х В}.

Если представить множества А и В при помощи кругов Эйлера, то разность А\В изобразится заштрихованной областью (рис. 10).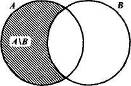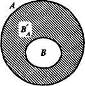


Рис. 10 Рис. 11

В школьном курсе математики чаще всего приходится выполнять вычитание множеств в случае, когда одно из них является подмножеством другого, при этом разность множеств А\В называют дополнением множества В до множества А, и обозначают символом В^/_А, а наглядно изображают так, как представлено на рисунке 11.

Определение. Пусть В с А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В.

Как уже было сказано, в случае когда В A, A\B = В^/_А.

Из определения следует, что В^/_А = {х | х А и х В}.

Выясним, как находить дополнение подмножества на конкретных примерах.

Если элементы множеств А и В перечислены и В А, то, чтобы найти дополнение множества В до множества А, достаточно перечислить элементы, принадлежащие множеству А и не принадлежащие множеству В. Так, если А = {1, 2, 3, 4, 5}, а В = {2,4},то В^/_А = {1,3,5}.

В том случае, когда указаны характеристические свойства элементов множеств А и В и известно, что В А, то множество В^/_А задают также с помощью характеристического свойства, общий вид которого «х А и х В». Так, если А - множество четных чисел, а В - множество чисел, кратных 4, то В^/_А - это множество, содержащее такие четные числа, которые не делятся на 4. Например, 22 В^/_А, т.к. 22 А (т.е. оно четное) и 22 В (т.е. оно не кратно 4).

Вычитание - это третья операция над множествами, с которыми мы уже познакомились. Нам известно, что пересечение множеств более сильная операция, чем объединение. А как быть с вычитанием? Например, каков порядок выполнения действий в выражении А\В С? Условились считать, что пересечение - более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении А\В С такой: сначала находят пересечение множеств В и С, а затем полученное множество вычитают из множества А.

Что касается объединения и вычитания множеств, то их считают равноправными. Например, в выражении А\ В С надо сначала выполнить вычитание (из А вычесть В), а затем полученное множество объединить с множеством С.

Вычитание множеств обладает рядом свойств. В частности, можно доказать, что для любых множеств А, В и С справедливы следующие равенства:

1) (А\В)\С = (А\С)\В;

2) (А В) \С=(А\С) (В\С);

3) (А\В) С=(А С) \(В С);

4) А\(В С)=(А\В) (А\С);

5) А\(В С)+(А\В) (А\С).
9. Понятие разбиения множества на классы

Понятия множества и операций над множествами позволяют уточнить наше представление о классификации - действии распределения объектов по классам.

Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса - четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.

Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество X разбито на классы X₁, Х₂,..., Х_п, если:

1) подмножества X₁, Х₂,..., Х_п попарно не пересекаются;

2) объединение подмножеств X₁, Х₂,..., Х_п совпадает с множеством X.

Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, если из множества X треугольников выделить подмножества равнобедренных, равносторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмножества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять мри помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Положим, что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда

про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества натуральных чисел (рис. 12). Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.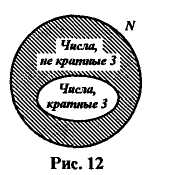


Вообще, если на множестве X задано одно свойство, то это множество разбивается на два класса. Первый- это класс объектов, обладающих этим свойством, а второй- дополнение первого класса до множества X. Во втором классе содержатся такие объекты множества X, которые заданным свойством не обладают. Такую классификацию называют дихотомической.

Рассмотрим теперь ситуацию, когда для элементов множества заданы два свойства. Например, какие свойства натуральных чисел, как «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N натуральных чисел можно выделить дна подмножества: А - подмножество чисел, кратных 3, и В - подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13).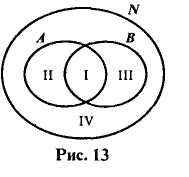



Проанализируем получившийся рисунок. Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей - на рисунке они пронумерованы. Каждая область изображает некоторое подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II - из чисел, кратных 3 и не кратных 5; подмножество III -из чисел, кратных 5 и не кратных 3; подмножество IV- из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14):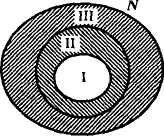


Рис. 14
I - класс чисел, кратных 6; II - класс чисел, кратных 3, но не кратных 6; III - класс чисел, не кратных 3.
10. Декартово произведение

Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.

Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а; b). Элемент а называют первой координатой (компонентой) пары, а элемент b - второй координатой (компонентой) пары.

Пары (а; b) и (с; d) равны в том и только в том случае, когда a =c и b = d.

В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).

Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, 4 = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая- множеству В. Если мы перечислим все такие пары, то получим множество:

{(1;3),(1;5),(2;5),(3;3),(3;5)}.

Видим, что имея два множества А и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств Аи В.

Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.

Декартово произведение множеств А и В обозначают Ах В. Используя это обозначение, определение декартова произведения можно записать так:

А х В= {(х;у) |х А и у В}.

З а д а ч а 1. Найдите декартово произведение множеств А и В, если:

a)A = {m;p},B={e,f,k};

б)А=В={3,5}.

Решение. а) Действуем согласно определению- образуем все пары, первая компонента которых выбирается из А, а вторая - из В:

А х В= {( m; е), (m; f), (m; k), (p; e), (p;f), (p; к)}.

б) Декартово произведение равных множеств находят, образуя всевозможные пары из элементов данного множества:

А х А={(3;3), (3;5), (5;3), (5;5)}

Операцию нахождения декартова произведения множеств называют декартовым умножением. Выясним, какими свойствами обладает эта операция. Так как декартовы произведения А х В и В х А состоят из различных элементов, то декартово умножение множеств А и В свойством коммутативности не обладает. Можно доказать, что для декартова умножения не выполняется и свойство ассоциативности. Но декартово произведение дистрибутивно относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства:

(А В) х С = (А х С) (В х С),

(А \ В) х С = (А х В) \ (В х С).

З а д а ч а 2. Проверьте справедливость свойства дистрибутивности декартова умножения относительно объединения, если:

А = {3; 4; 5}, В ={5; 7}, С ={7; 8}.

Решение. Найдем объединение множеств А и В: А В = {3,4,5,7}. Далее перечислим элементы множества (А В) х С, используя определение декартова произведения: (А В) х С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.

Чтобы найти элементы множества (А х С) (В х С), перечислим сначала элементы множеств А х С и В х С:

А х С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8)}

В х С={(5;7),(5;8),(7;7),(7;8)}.

Найдем объединение полученных декартовых произведений: (А х С) (В х С) = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.

Видим, что множества (А В) х С и (А х С) (В х С) состоят из одних и тех же элементов, следовательно, для данных множеств А, В и С справедливо равенство (А В) х С = = (А х С) (В х С).

Выясним теперь, как можно наглядно представлять декартово произведение множеств.

Если множества А и В конечны и содержат небольшое число элементов, то можно изобразить декартово произведение этих множеств при помощи графа или таблицы. Например, декартово произведение множеств А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке 17(а, б).

В А	3	5
1	(1,3)	(1,5)
2	(2,3)	(2,3)
3	(3,3)	(3,3)

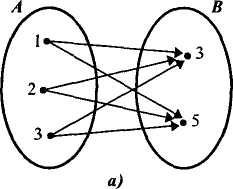б) Рис. 17

Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение А хВ множеств А = {1, 2, 3} и В = = (3, 5} на координатной плоскости будет выглядеть так, как показано на рисунке 18.

у
5
3


0 1 2 3 х Рис.18

Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В - на оси Оу.

Такой способ наглядного представления декартова произведения двух числовых множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.

Задача 3. Изобразить на координатной плоскости декартово произведение Ах В, если:

а) А = {1,2,3},В = [3,5];

б) А = [1,3], В = [3,5];

в) A = R, В = [3,5];

г) А = R, В = R.

Р е ш е н и е, а) Так как множество А состоит из трех элементов, а множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декартово произведение А х В будет состоять из бесконечного множества нар, первая компонента которых либо 1, либо 2, либо 3, а вторая-любое действительное число из промежутка [3, 5]. Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками (рис. 19).

у
5
3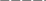


0 1 2 3 х Рис. 19

б) В этом случае бесконечны оба множества А и В. Поэтому первой координатой пары, принадлежащей множеству Ах В, может быть любое число из промежутка [1,3], и, следовательно, точки, изображающие элементы декартова произведения данных множеств А и В, образуют квадрат (рис. 20).

у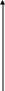
5
3




0 1 2 3 х Рис. 20

Чтобы подчеркнуть, что элементы декартова произведения изображаются и точками, лежащими внутри квадрата, этот квадрат можно заштриховать.

в) Этот случай отличается от предыдущего тем, что множество А состоит из всех действительных чисел, т.е. абсцисса точек, изображающих элементы множества А х В, принимает все действительные значения, в то время как ордината выбирается из промежутка [3,5]. Множество таких точек образует полосу (рис. 21).

у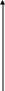
5
3




0 х Рис. 21
г) Декартово произведение R x R состоит из всевозможных действительных чисел. Точки, изображающие эти пары, сплошь заполняют координатную плоскость. Таким образом, декартово произведение R x R содержит столько же элементов, сколько точек находится на координатной плоскости.

В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367- это упорядоченный набор из трех элементов, а запись слова «математика» - это упорядоченный набор из 10 элементов.

Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа - это число элементов, из которых он состоит. Например, (3; 6; 7) - это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) - это кортеж длины 10.

Рассматривают в математике и декартово произведение трех, четырех и вообще и множеств.

Определение. Декартовым произведением множеств A₁, А₂,..., А_n называется множество всех кортежей длины n, первая компонента которых принадлежит множеству A₁, вторая - множеству А₂,..., n-я - множеству An.

Декартово произведение множеств A₁, А₂,..., А_nобозначают так: A₁ х А₂ х... х А_n.

З а д а ч а 4. Даны множества: A₁ = {2, b), А₂ = {3, 4, 5}, А₃ = {6,7}. Найти A₁ х А₂ х А₃.

Ре ш е н и е. Элементами множества A₁х А₂х А₃ будут кортежи длины 3 такие, что первая их компонента принадлежит множеству A1, вторая - множеству А₂, третья - множеству А₃.

A₁х А₂х А₃ = {(2, 3, 6), (2, 3, 7), (2, 4, 6), (2, 4, 7),

(2, 5, 6), (2, 5,7), (3,3,6), (3,3, 7),

(3,4, 6), (3,4,7), (3,5,6), (3,5,7)}.