методика математики книга. Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.58 Mb.
|
Математичні ранки сприяють вихованню позитивних рис характеру учнів, 'збуджують прагнення більше знати. Математичний ранок у початкових класах — це свято, яке старанно готують і дорослі, і діти. Підготовка ранку навчає і виховує такою ж мірою, як і сам ранок. Вдалий розподіл завдань і обов'язків відповідно до здібностей та інтересів учнів дасть їм змогу максимально виявити ініціативу і фантазію, сприятиме підвищенню ефективності математичного ранку. У початковій школі бажано практикувати 5 математичних ранків: один у 2 класі і по два у 3 та 4 класах. У 2 класі ранок проводиться у другому півріччі навчального року, а у 3 і 4 класах — по одному в кожному півріччі. Математичний ранок — свято, основу якого становлять командні й парні змагання на математичному матеріалі певного класу. Новий і позапрограмовий матеріал має бути, але у невеликому обсязі і в цікавій формі. Зміст і форма математичних ранків можуть бути різні, але треба домагатися, щоб кожен учень був не тільки глядачем свята, а й активним його учасником. На математичному ранку мусять працювати і сильні, і слабкі учні. Свято має відбуватися весело, жваво. Математичні ранки присвячують закінченню вивчення певного розділу програми, важливим народним чи державним подіям, визначним українським математикам. Цей захід — один з видів художньої самодіяльності. Він потребує ґрунтовної підготовки. Ще під час уроків учитель має опрацювати основні форми змагань та ігор, що використовуватимуться на цьому святі. Іноді потрібні будуть і репетиції у позаурочний час. Відповідно до набуття досвіду підготовки і проведення математичних ранків можна буде до цієї роботи залучати і декого з батьків. Методика викладання математики в початкових класах 301 Ранок відбувається в класі (якщо проводиться для одного класу) або у шкільному залі (якщо у святі беруть участь два класи). Приміщення святково прикрашають, розвішують портрети вчених-математиків, висловлювання про математику, цікаві запитання і задачі, ребуси, лабіринти тощо. Здебільшого учасники математичного ранку поділяються на дві групи. Дві групи — це два паралельні класи або один клас, поділений на дві групи. З кожної групи виділяється команда гравців (5-10 учнів). Інші учні з групи виконують роль активних вболівальників чи резерву підтримки. Кожна команда обирає собі назву (можна назву і девіз). Один з групи учнів виконує роль капітана команди. Кожного разу обирають нового капітана. Тому з ними необхідно проводити додаткову роботу. Капітани команд мусять мати достатньо чіткі уявлення про сценарій математичного ранку. У приміщенні школярі розміщуються за "принципом": одна група зліва, друга — справа. Учні, які входять до складу команд, сідають останніми (для зручності виходу до дошки). Тексти математичних завдань подають різними способами, але найкраще — на окремих заздалегідь підготовлених таблицях. Як правило, числові дані завдань добираються так, щоб обчислення можна було виконувати усним способом. Здебільшого розв'язання завдань учні виконують про себе, записуючи чи повідомляючи тільки відповіді. Пояснення чи коментування подаються лише на вимогу ведучого. Роль ведучого на математичному ранку виконує вчитель. Ведучий — це режисер, він остаточно схвалює сценарій математичного ранку, вносить до нього корективи в ході проведення. Роль ведучого треба проводити у мажорному тоні, підбадьорюючи і підтримуючи гравців. За правильне розв'язання математичного завдання гравцю чи команді зараховується певна кількість очок. Команді, яка виконала завдання швидше або красивіше, зараховується додатково одне очко. Переможців здебільшого визначає ведучий, але можна й призначити суддів. Бажано визначити премії переможцям. Це можуть бути кольорові листівки з підписами, чисті учнівські зошити, олівці тощо. Ще краще, щоб кожен учень отримав сувенір, наприклад, книжку з цікавими задачами і вправами з математики для даного класу (їх мають заздалегідь закупити батьки). Ранок проводиться на III і IV уроках навчального дня. Безпосередньо дійова частина ранку займає одну годину, решта часу йде на розгляд висловлювань про математику, ознайомлення із завданнями, розвішаними на стінах, організаційний момент та на підбиття підсумків змагання і проведення коротеньких бесід виховного спрямування на матеріалі числових даних чи математичних фактах. Можна також підсумовувати навчальну роботу за півріччя. Змістом математичних завдань є звичайні приклади на 1-3 дії, вправи на знаходження значень виразів з буквеним компонентом, рівняння на одну (іноді дві) операції, прості і складені арифметичні задачі, задачі підвищеної складності, логічні задачі, вправи з геометричним матеріалом. Зовнішня302 Розділ XV. Позакласна робота з математики особливість завдань — це цікава і наочна форма подання їх змісту, можливість порівняльного ефекту. Розробка ранку подається у вигляді сценарію. Подамо опис (сценарій) математичного ранку, проведеного у 2 класі (Український коледж ім. В. Сухомлинського, вчителька Т.Г. Хайруліна). Ведучий: Діти, сьогодні у нас буде незвичайне свято-змагання — математичний ранок. Наша мета — показати свою кмітливість, винахідливість і знання з математики. Команди, які будуть змагатись, і вболівальники візьмуть участь у розв'язуванні задач, прикладів і цікавих завдань. Перш за все, послухаємо і подивимось привітання команд. На сцені шикуються команди. Назва першої команди — "Сонечко", назва другої — "Усмішка". Вітання команд і проголошення девізів Капітан команди "Сонечко": "Наш девіз!". Гравці разом: "Раз, два, три, чотири, п'ять. Вміють діти рахувать. І яскраве сонце сяє, Щоб наш настрій піднімать". Капітан команди "Усмішка": "Наш девіз!". Гравці разом: "Скільки усмішок навкруг. Ти — мій друг, і я — твій друг. Будем разом рахувать, Розважатись, жартувать". Ведучий: Молодці команди. Тепер проведемо з вами математичну ізминку. /. Знайди шлях у лабіринті. На дошці малюнки двох лабіринтів (мал.168).  Мол. 168 Ведучий: Казкові герої Колобок і біле ведмежа Умка пішли погуляти. Проте їх спіткало лихо: вони заблукали. Щоб допомогти героям казок Методика викладання математики в початкових класах 303 потрапити додому, команди мають знайти шляхи у лабіринтах. Хто готовий показати шлях казковому герою, піднімає руку. (Ведучий визначає, хто буде відповідати, і викликає цього гравця до дошки). //. Математична естафета. Ведучий: Наступним змаганням буде математична естафета. Математична естафета — це змагання команд. Команди шикуються в дві колони. За сигналом ведучого перші гравці підбігають до дошки, де записана умова прикладів, розв'язують два перших приклади і повертаються до своєї команди. Вони торкаються рукою наступного гравця, після чого той приймає естафету і прямує до дошки розв'язувати наступних два приклади. І так до кінця. Виграє команда, яка швидше і правильніше виконає завдання. Завдання для першої командиЗавдання для другої команди 34 +17 44 - 26 66 +19 37 - 28 45 - 29 94 - 67 84 - 38 23 + 69 61-17 59+ 18 81-13 29 + 16 70-31 80-16 92-44 100-17 52 + 28 _ 33 + 28 73 +17 34 + 58 Ведучий: Поки команди трохи відпочинуть, позмагаються вболівальники. У них буде можливість надати допомогу команді, за яку вони вболівають. III. "Риболови". На набірному полотні розставлені приклади і зверху закриті фігурами рибок. і 45 + 5 23 + 18 78 + 13 і 63 - 25 84-29 58 - 34 Ведучий: На сцену я викликатиму вболівальників (одного — вболіваль-„лка команди "Сонечко", іншого — вболівальника команди "Усмішка"). (Учасників можна визначати за допомогою жеребкування). Вболівальник знімає рибку з дошки і розв'язує приклад, схований за цією рибкою. Якщо приклад він розв'язав правильно, то віддає "зловлену" рибку капітану команди, за яку вболіває. Так викликають 3 пари вболівальників. Ведучий: Наступний конкурс. IV. "Розв'яжи задачу-вірш". Вболівальники команд для своїх суперників підготували по дві задачі-вірші. Зараз ми їх послухаємо. Кожен з учнів розкаже задачу-вірш. Вболівальники команди-суперника слухають цю задачу і розв'язують її. Учні, які знайшли відповідь, піднімають руку. Ведучий обирає, хто із вболівальників буде відповідати. Задачі-вірші Для першої командиДля другої команди йі Гнав Івась телят до річки лі Сім бичків і три телички. у$„ Хай вони поп'ють води. ■щ Полічи теляток ти. ■?;;' Посадив татусь Миколи "18 штук квасолин. А сердиті 5 індиків Взули нові черевики. Рипу-рипу, походжають. Скільки всіх, вони не знають. 13 мавпочок у клітках — Дорослі є і мавпи-діти, 304 Розділ XV. Позакласна робота з математики 9 виткнулись з землі. Дорослих мавп у клітці — 5. Скільки штук ще не зійшли? А скільки там є мавпенят? Ведучий: Команди відпочили і тепер продовжать змагання. Зараз ми перевіримо, як команди вміють розв'язувати задачі. V. Конкурс команд. На дошці розміщено короткі записи задач (мал. 169). Для першої командиДля другої команди  Мал. 169 Ведучий: Послухайте уважно задачі (він розповідає зміст кожної задачі). Кожна задача на дві дії. Гравцям треба записати ці дії, виконати обчислення і пояснити, про що вони дізналися у кожній дії. Капітани команд призначають, хто з гравців їхньої команди буде розв'язувати задачу. VI. Конкурс уболівальників "Розгадайребус". Ведучий: Наступний конкурс знову для вболівальників. Потрібно розв'язати ребуси. (Викликають по черзі трьох уболівальників кожної команди, вони дають відповіді з місця). Для першої команди Для другої команди 7'я (сім'я) -р>^,„..- ЮОляр (столяр) тіЮО (тісто) V""" 40а (сорока) акЗса (актриса) ! , віЗна (вітрина) VII. Конкурс капітанів. Ведучий: Наступний наш конкурс — конкурс капітанів. Ми з вами визначимо, хто з наших капітанів уважніший. У мене в руках "Загадковий пакет". У ньому знаходяться різні геометричні фігури (круги, квадрати, прямокутники, п'ятикутники). Капітани (по черзі) за моїм завданням, не дивлячись у пакет, а тільки опустивши в нього руку, повинні знайти там відповідну до назви геометричну фігуру. Виграє той, хто дасть більше правильних відповідей. (Пакет з одного боку прозорий, щоб уболівальники могли спостерігати за тим, як капітани виконують завдання). Методика викладання математики в початкових класах 305 VIII. Конкурс "Жива нумерація". Ведучий: У цьому конкурсі візьмуть участь змішані команди, бо до команд ми додамо по кілька вболівальників. Всього за кожну команду буде виступати по 10 учасників. Скільки вболівальників треба запросити до кожної команди? (Правильно, ще по 5 учнів). На грудях у гравця буде одна з десяти цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Гравці команд сідають на спеціально поставлені стільці або лаву відповідно зліва і справа від двох пар стільців, на яких будуть "записуватися" числа. Кожній парі учнів треба буде сісти так, щоб цифри на їх грудях утворювали назване число чи потрібну відповідь. До стільців гравці не біжать, а йдуть після команди ведучого: "Можна йти". Завдання: 1. Записати числа: 18, 23, 45. 2. Записати числа, кожне з яких на 4 більше від того, яке я скажу: 6, 20, 9. 3. Записати відповіді до названих мною прикладів: 70+10 72-2 14 + 25 Ведучий: Поки судді підраховують кількість балів кожної команди, ми з вами поговоримо про ті написи і задачі, які прикрашають сьогодні наше приміщення. Люди здавна високо цінували значення математики. Про це свідчить велика кількість цікавих і мудрих висловів, присвячених цій науці. Так, стародавні греки називали математику гімнастикою розуму. А видатний український педагог Василь Олександрович Сухомлинський стверджував: "Розумова праця на уроках математики — пробний камінь мислення". Діти, а хто з вас встиг розв'язати задачі, зображені малюнками? Почнемо із задачі, малюнок до якої зображено ліворуч (мал. 170). Хто може відповісти, скільки літрів води вміщують банка і бідон окремо, і пояснити свою відповідь? (Відповідають бажаючі). Добре, спробуйте розв'язати задачу, зображену праворуч (мал. 171). Скільки слив треба перекласти": 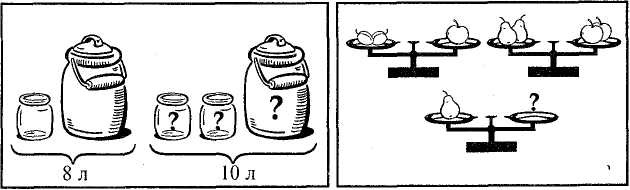 Мал. 170 Мал. 171 Хто знає, скільки слив треба покласти на праву шальку терезів, щоб врівноважити одну грушу? (Відповідають бажаючі). Ведучий: На цьому наше математичне свято закінчується. Команда "Сонечко" набрала 20 балів, а команда "Усмішка" — 18 балів. Підіб'ємо підсумки змагань. Виграла команда "Сонечко". Ваші оплески переможцям. Вручення призів. 306 Розділ XV. Позакласна робота з математики § 52. Математичні олімпіади Математичні олімпіади молодших школярів мають пропедевтичний характер. Основними рівнями олімпіад учнів початкових класів є класні та шкільні. Міжшкільні чи районні проводяться за умов належної уваги працівників методичних кабінетів. Першою особливістю математичних олімпіад молодших школярів і необхідною умовою їх ефективності є масовість. Кожному учню має бути надана можливість узяти в ній участь. Реальним заходом забезпечення масовості є організація і проведення класних олімпіад. Друга особливість і друга необхідна умова ефективності олімпіад молодших школярів — опосередкована та безпосередня участь батьків у їх підготовці. Реально цього можна досягти, якщо протягом певного часу учням під час підготовки пропонується розв'язати вдома деяку кількість "нестандартних" задач. Зрозуміло, що процес опрацювання нестандартних задач охоплюватиме консультації і допомогу з боку батьків чи старших братів і сестер. Третьою особливістю і важливою умовою здійснення математичних олімпіад молодших школярів є повне забезпечення вчителя задачним матеріалом як до змісту завдань самої олімпіади, так і до завдань підготовчої роботи. Реальний захід — видання відповідного друкованого посібника масовим тиражем. Учителю потрібно буде лише уточнити, скоротити або доповнити "задачну систему" відповідно до умов роботи з учнями свого класу. Четверта особливість і необхідна вимога — проведення олімпіади в умовах режиму, коли кожний учасник має впоратися успішно, тобто розв'язати хоча б одну задачу. Більшість учнів має впоратися з двома-трьома задачами. Переможцями слід вважати третину учнів, яка має кращі результати у розв'язанні задач олімпіади. Розв'язування всіх задач не є вимогою для переможців. Усім учасникам олімпіади оголошується подяка і даруються листівки з відповідними записами. П'ятою особливістю можна вважати поступовість у нарощуванні турів олімпіад. У 2 класі проводяться тільки класні олімпіади. У 3 класі проводяться класні і шкільні, а в 4 класі — класні, шкільні і міжшкільні (районні). Усі класні олімпіади бажано провести 5 — 15 квітня, шкільні — 16 — 25 квітня. Якщо олімпіада продовжуватиметься і на міжшкільному рівні, то її можна провести 5—15 травня. Час проведення класних і шкільних олімпіад має бути узгоджений і затверджений керівниками школи. Для проведення шкільного туру бажано визначити організатора. Обсяг і зміст задач кожної математичної олімпіади варто розглянути на засіданні методичної комісії вчителів початкових класів. Бажано, щоб початок (відкриття) олімпіади (і класної, і шкільної) був офіційно-урочистим. Приміщення слід святково прикрасити, доцільно виготовити методико-математичний лозунг: "Математика — гімнастика розуму", "Над задачею треба думати", "Задачі — це шлях у математику". Добре, якщо буде присутній дехто з батьків. (Змагаються їхні діти^ Методика викладання математики в початкових класах 307 Відкриває олімпіаду хтось із керівників школи; вчитель математики, керівник методичного об'єднання вчителів початкових класів або вчитель-пенсіонер бажає дітям успіхів у математичних змаганнях. В учнів на партах лежать чисті подвійні аркуші паперу в клітинку, аркуші для чернеток, лінійки. За вказівкою вчителя учні підписують аркуші, на яких вони будуть записувати розв'язання задач (на класних олімпіадах — прізвище та ім'я, на шкільних — клас, прізвище та ім'я). Учитель роздає учням картки з текстами задач олімпіади чи ознайомлює їх із задачами за записами на дошках. Він пропонує їм одразу прочитати всі задачі (крім резервної) і запитати, якщо є щось незрозуміле. Далі вчитель подає коротку інструкцію. Всього задач 6, але кожен розв'язує стільки, скільки зможе (і скільки встигне) за відведений час (40 - 50 хв). Розв'язувати задачі можна у будь-якому порядку. В разі потреби можна користуватися чернетками. Умову задач не треба переписувати. Перед записом розв'язання необхідно писати номер задачі (задача 1, задача 5). Підручниками з математики користуватися можна. Якщо у процесі роботи виникне запитання, то слід підняти руку. Відповідь учню вчитель дає персонально. На час розв'язування задач потрібно підтримувати в учнів спокійно-діловий, але бадьорий настрій. Учитель і присутні мають бути особливо тактовні, підтримувати дітей морально, а в окремих випадках (окремим учням) надавати методичну допомогу. Через 20-25 хв варто провести фізкультхвилинку (не менш як на 2 хв). Після закінчення відведеного часу вчитель збирає аркуші з розв'язаннями задач, дякує учням за участь в олімпіаді. Перевіряє роботи школярів вчитель. На нашу думку, необов'язково підкреслювати і виправляти помилки. Достатньо буде, якщо вчитель щодо кожної задачі у кожній роботі зробить для себе такі помітки: "+" — задача розв'язана правильно; "н" — розв'язування задачі не закінчено чи допущено помилку; "—" — задача не розв'язана або учень не приступив до її розв'язування. Слід додатково зробити позначки про оригінальність розв'язування задачі. Результативність робіт учнів можна оцінювати у зручний для самого вчителя спосіб. Зокрема, так: а) у звичайних шкільних балах; б) у балах за підрахунками очок — розв'язування кожної задачі оцінюється від 1 до 4 очок; в) шляхом ранжування: успішно пройшов старт — розв'язав 1 - 2 задачі; успішно подолав більшу частину дистанції — розв'язав 3 — 4 задачі; успішно наблизився до фінішу — розв'язав 5 і більше задач. Якщо вчитель буде повертати роботи учням, то варто скористатися записами: "зараховано", "добре", "відмінно". За результатами перевірки класної олімпіади у 3 і 4 класах треба визначити третину учнів (переможців) для участі у шкільній олімпіаді, підготувати стислу інформацію про загальні результати учнів класу та оригінальні способи розв'язування задач окремими учнями: зазначити, які задачі варто опрацювати на уроці (для підготовки до шкільної олімпіади). Особливість шкільної олімпіади полягає в тому, що в ній бере участь тільки третина учасників класної олімпіади. Задачі для шкільної олімпіади пропонуються тільки в одному варіанті. Учасники олімпіади мають сидіти306 Розділ XV. Позакласна робота з математики § 52. Математичні олімпіади Математичні олімпіади молодших школярів мають пропедевтичний характер. Основними рівнями олімпіад учнів початкових класів є класні та шкільні. Міжшкільні чи районні проводяться за умов належної уваги працівників методичних кабінетів. Першою особливістю математичних олімпіад молодших школярів і необхідною умовою їх ефективності є масовість. Кожному учню має бути надана можливість узяти в ній участь. Реальним заходом забезпечення масовості є організація і проведення класних олімпіад. Друга особливість і друга необхідна умова ефективності олімпіад молодших школярів — опосередкована та безпосередня участь батьків у їх підготовці. Реально цього можна досягти, якщо протягом певного часу учням під час підготовки пропонується розв'язати вдома деяку кількість "нестандартних" задач. Зрозуміло, що процес опрацювання нестандартних задач охоплюватиме консультації і допомогу з боку батьків чи старших братів і сестер. Третьою особливістю і важливою умовою здійснення математичних олімпіад молодших школярів є повне забезпечення вчителя задачним матеріалом як до змісту завдань самої олімпіади, так і до завдань підготовчої роботи. Реальний захід — видання відповідного друкованого посібника масовим тиражем. Учителю потрібно буде лише уточнити, скоротити або доповнити "задачну систему" відповідно до умов роботи з учнями свого класу. Четверта особливість і необхідна вимога — проведення олімпіади в умовах режиму, коли кожний учасник має впоратися успішно, тобто розв'язати хоча б одну задачу. Більшість учнів має впоратися з двома-трьома задачами. Переможцями слід вважати третину учнів, яка має кращі результати у розв'язанні задач олімпіади. Розв'язування всіх задач не є вимогою для переможців. Усім учасникам олімпіади оголошується подяка і даруються листівки з відповідними записами. П'ятою особливістю можна вважати поступовість у нарощуванні турів олімпіад. У 2 класі проводяться тільки класні олімпіади. У 3 класі проводяться класні і шкільні, а в 4 класі — класні, шкільні і міжшкільні (районні). Усі класні олімпіади бажано провести 5 — 15 квітня, шкільні — 16 — 25 квітня. Якщо олімпіада продовжуватиметься і на міжшкільному рівні, то її можна провести 5—15 травня. Час проведення класних і шкільних олімпіад має бути узгоджений і затверджений керівниками школи. Для проведення шкільного туру бажано визначити організатора. Обсяг і зміст задач кожної математичної олімпіади варто розглянути на засіданні методичної комісії вчителів початкових класів. Бажано, щоб початок (відкриття) олімпіади (і класної, і шкільної) був офіційно-урочистим. Приміщення слід святково прикрасити, доцільно виготовити методико-математичний лозунг: "Математика — гімнастика розуму", "Над задачею треба думати", "Задачі — це шлях у математику". Добре, якщо буде присутній дехто з батьків. (Змагаються їхні діти^ Методика викладання математики в початкових класах 307 Відкриває олімпіаду хтось із керівників школи; вчитель математики, керівник методичного об'єднання вчителів початкових класів або вчитель-пенсіонер бажає дітям успіхів у математичних змаганнях. В учнів на партах лежать чисті подвійні аркуші паперу в клітинку, аркуші для чернеток, лінійки. За вказівкою вчителя учні підписують аркуші, на яких вони будуть записувати розв'язання задач (на класних олімпіадах — прізвище та ім'я, на шкільних — клас, прізвище та ім'я). Учитель роздає учням картки з текстами задач олімпіади чи ознайомлює їх із задачами за записами на дошках. Він пропонує їм одразу прочитати всі задачі (крім резервної) і запитати, якщо є щось незрозуміле. Далі вчитель подає коротку інструкцію. Всього задач 6, але кожен розв'язує стільки, скільки зможе (і скільки встигне) за відведений час (40 - 50 хв). Розв'язувати задачі можна у будь-якому порядку. В разі потреби можна користуватися чернетками. Умову задач не треба переписувати. Перед записом розв'язання необхідно писати номер задачі (задача 1, задача 5). Підручниками з математики користуватися можна. Якщо у процесі роботи виникне запитання, то слід підняти руку. Відповідь учню вчитель дає персонально. На час розв'язування задач потрібно підтримувати в учнів спокійно-діловий, але бадьорий настрій. Учитель і присутні мають бути особливо тактовні, підтримувати дітей морально, а в окремих випадках (окремим учням) надавати методичну допомогу. Через 20-25 хв варто провести фізкультхвилинку (не менш як на 2 хв). Після закінчення відведеного часу вчитель збирає аркуші з розв'язаннями задач, дякує учням за участь в олімпіаді. Перевіряє роботи школярів вчитель. На нашу думку, необов'язково підкреслювати і виправляти помилки. Достатньо буде, якщо вчитель щодо кожної задачі у кожній роботі зробить для себе такі помітки: "+" — задача розв'язана правильно; "н" — розв'язування задачі не закінчено чи допущено помилку; "—" — задача не розв'язана або учень не приступив до її розв'язування. Слід додатково зробити позначки про оригінальність розв'язування задачі. Результативність робіт учнів можна оцінювати у зручний для самого вчителя спосіб. Зокрема, так: а) у звичайних шкільних балах; б) у балах за підрахунками очок — розв'язування кожної задачі оцінюється від 1 до 4 очок; в) шляхом ранжування: успішно пройшов старт — розв'язав 1 - 2 задачі; успішно подолав більшу частину дистанції — розв'язав 3 — 4 задачі; успішно наблизився до фінішу — розв'язав 5 і більше задач. Якщо вчитель буде повертати роботи учням, то варто скористатися записами: "зараховано", "добре", "відмінно". За результатами перевірки класної олімпіади у 3 і 4 класах треба визначити третину учнів (переможців) для участі у шкільній олімпіаді, підготувати стислу інформацію про загальні результати учнів класу та оригінальні способи розв'язування задач окремими учнями: зазначити, які задачі варто опрацювати на уроці (для підготовки до шкільної олімпіади). Особливість шкільної олімпіади полягає в тому, що в ній бере участь тільки третина учасників класної олімпіади. Задачі для шкільної олімпіади пропонуються тільки в одному варіанті. Учасники олімпіади мають сидіти308 Розділ XV. Позакласна робота з математики по одному за партами чи столами. У школах, де є паралельні класи, істотна особливість олімпіади полягає у тому, що разом працюють учні різних класів. В організації шкільної олімпіади беруть участь учителі математики і керівники шкіл. Про результати шкільної олімпіади у 4 класах і можливих учасників міжшкільної олімпіади не зайвим буде оголосити наказом по школі. На міжшкільну чи районну олімпіаду варто визначити третину від учасників шкільної олімпіади у 4 класах. Подамо зміст завдань класних олімпіад (перший варіант) та зразки завдань шкільного (3 і 4 класи) і міжшкільного (4 клас) турів. 2 клас 1. Утвори двоцифрові числа, використовуючи тільки цифри 0, 2, 5 і 7. У кожному числі цифри мають бути різні. Всі числа записати у порядку від меншого до більшого. ■•■ 2. Серед чисел 7, 10, 12, 15, 18, 23, 27, 30 знайди такі три числа, сума яких дорівнює 50. 3. Роман розповідав сестрі про зустріч з футболу команд "Шахтар" і "Карпати": — У першому таймі з рахунком 2 : 1 виграли "Карпати", але у другому таймі виграла команда "Шахтар" з рахунком 4 : 2. — А яка команда перемогла? — запитала сестра. Що мав відповісти Роман? 4. Від дуба до сосни 62 м. їжак ішов від дуба до сосни, а назустріч йому — Заєць. Хто з них був дальше від дуба і на скільки метрів, коли їжак пройшов 18 м, а Заєць - 43 м? 5. До годівниці спочатку прилетіло 10 голубів, потім горобці. Голубів було на 4 більше, ніж горобців. Скільки всього птахів прилетіло? 6. Накресли який-небудь прямокутник і поділи його двома відрізками на З трикутники і один п'ятикутник. Резервна. Три дошкільниці Галинка, Маринка й Олеся прийшли на святковий ранок у сукнях різного кольору: жовтого, рожевого й синього. Галинка була не в жовтій сукні, Маринка - не в жовтій і не в рожевій. У сукні якого кольору була кожна дівчинка? 3 клас 1. Запиши всі трицифрові числа, використовуючи тільки цифри 0, 3 і 7. Повторювати цифри можна. 2. Використовуючи чотири рази цифру 5, знаки дій і дужки, запищи число ЗО. 3. На біговій доріжці рівномірно поставлені стовпи. Від першого до четвертого стовпа бігун добіг за 12 с. Через скільки секунд після цього бігун буде біля сьомого стовпа? (Швидкість бігу однакова). 4. Дівчатка мали посадити 24 кущі аґрусу, малини і смородини. Кущів аґрусу мало бути стільки, скільки кущів малини, а кущів смородини — у 2 рази більше, ніж аґрусу. Скільки кущів кожного виду посадили дівчатка? 5. Два рибалки вирішили зварити на вогнищі юшку. Перший рибалка дав 5 рибин, а другий — 4. Тільки вони зварили, як підійшов мисливець. За свою порцію юшки він дав їм 18 грибів. Як рибалки мають поділити ці гриби між собою? 6. З чотирьох однакових квадратів склади один великий. Знайди його периметр, якщо периметр малого квадрата дорівнює 8 см.« Методика викладання математики в початкових класах Ш- Резервна. Є каструлі на 5 л і 3 л. Потрібно набрати з річки 4 л води. Шкільний тур (3 клас) ., 1. Скільки треба цифрових знаків, щоб пронумерувати зошит у 100 сторінок? ■ 2. Розстав дужки так, щоб рівності були правильними: 4 + 6 • 3 = 30 30 - 10 - 3 = 24 18 : 6 ■ 3 + 3 = 12 3. На складі є колоди однакової товщини завдовжки по 4 м і 5 м. Потрібно напиляти 20 колод по 1 м кожна. Одне перепилювання триває 1 хв. Чи можна виконати завдання за 15 хв? 4. Три білочки збирали горіхи. Перша білочка знайшла 8 горіхів, друга — 5, а третя — лише 2. Ці горіхи білочки поділили між собою порівну. Скільки горіхів віддала перша білочка третій? Друга білочка — третій? 5. Господарка хотіла купити кавун на 3 кг, а купила на 5 кг, тому заплатила на 1 грн. 20 коп. більше. Скільки коштував кавун? 6. Ширина смужки дорівнює 2 см. Від неї відрізали прямокутник з периметром 20 см. Знайди довжину прямокутника. Резервна. Десятилітровий бідон повний. Як з нього за допомогою семилітрового і трилітрового бідонів відлити 5 л води? 4 клас 1. Запиши всі чотирицифрові числа, які можна утворити з цифр 0 і 1. 2. У рівності однаковими буквами позначено однакові цифри: АБВГ |
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Бондаренко | + | + | | + | | + | | |
| Вакула | + | + | + | + | + | + | | |
Бажано, щоб до проведення класної олімпіади ця таблиця була заповнена не менш як на половину. Розв'язування окремих домашніх задач може бути здійснено і в класі. У тих випадках, коли у сім'ї не можна сподіватися на оптимальну організацію розв'язування домашніх задач, варто провести з учнями одне-два післяурочні заняття.
2 клас
ці. Запиши всі можливі двоцифрові числа за допомогою: а) цифр 2, 7 і 9; б) цифр 0, 3, 5 і 8 (повторювати цифри можна). .2. Учень записав підряд усі числа від 1 до 100. Скільки разів йому довелося ■писати цифру 8?
3. Якими п'ятьма монетами можна набрати 80 коп.?
4. Розстав цифри І, 2, 3, 4, 5, 6, 7, 8 і 9 по сторонах трикутника так, щоб їх сума н&< кожній стороні дорівнювала 20.
Вказівка. На одній стороні записано цифри 5, 2, 9 і 4.
5. Біля будинку ростуть 2 липи, 5 яблунь і 8 груш. Скільки всього плодових дерев росте біля будинку?
6. 5 хлопчиків і 18 дівчаток прибирали клас. Потім Марина, Івась і Таня пішли у сад поливати квіти. Скільки дівчаток залишилося у класі?
7. Братові 18 років, а сестрі 10 років. Скільки років буде братові, коли сестрі стане стільки років, скільки йому зараз?
8. У першій бригаді було 12 тракторів, а у другій — менше. Коли з першої у другу переїхало 4 трактори, то в обох бригадах тракторів стало порівну. Скільки тракторів було у другій бригаді спочатку?
9. У господарки було 12 гусей, тобто на 8 менше, ніж качок. Скільки качок і гусей було разом?
10. Півпериметр прямокутника дорівнює 50 см, а одна з його сторін — 30 см. На скільки сантиметрів довжина прямокутника більша, ніж його ширина?
11. Побудуй прямокутник і поділи його двома відрізками на 2 трикутники і 2 чотирикутники.
12. Забери одну паличку, щоб із чотирьох квадратів утворилося три (мал. 173).
Методика викладання математики в початкових класах
313
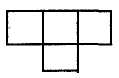Мал. 17313. 4 товариші спускалися з гори на санчатах. Ігор проїхав дальше, ніж Роман. Роман проїхав менше, ніж Олег, але дальше, ніж Вадим. Хто проїхав найменше?
14. Чотири товариші Іван, Мирон, Мишко і Сергій отримали за контрольну роботу оцінки "5", "4", "З". Сашко отримав оцінку вищу, ніж Іван, а Мирон — таку саму оцінку, як і Сергій. Хто з хлопчиків одержав "трійку"?
3 клас
1. Запиши всі трицифрові числа, використовуючи тільки цифри 1 і 9.
2. Дві дівчинки мали по 70 коп. У кожної було по 4 монети. У першої дівчинки були такі монети: 25 коп., 25 коп., 10 коп., 10 коп. Які монети були у другої дівчинки?
3. Використовуючи шість разів цифру 2 і знаки дій та дужки, запиши число 100.
4. Мама дала Яринці стільки п'ятаків, скільки серед чисел від 3 до 48 таких, які діляться на 3. Скільки грошей мама дала Яринці?
5. Хлопчик по прямій лінії забив у землю 6 кілочків. Відстань між кожними сусідніми кілочками дорівнює 6 м. Скільки метрів становить відстань між крайніми кілочками?
6. У багатоповерховому будинку від поверху до поверху 15 східців. Скільки східців треба пройти, щоб піднятися на третій поверх?
7. Для 2 коней і 12 корів видали 100 кг сіна. Кожному коневі видавали по 8 кг сіна. Скільки кілограмів сіна видавали кожній корові?
8. Маса молока в повному бідоні становить 34 кг. Маса молока в бідоні, наповненому наполовину, дорівнює 19 кг. Скільки кілограмів становить маса бідона?
9. Заєць на 3 кг важчий, ніж кріль. Маса 2 зайців така, як 5 кролів. Скільки кілограмів становить маса зайця?
10. Два хлопчики купували однакові зошити. Разом вони заплатили 100 коп., але перший з них заплатив на 20 коп. більше, ніж другий. Скільки копійок заплатили перший і другий хлопчики окремо?
11. Побудуй квадрат зі стороною 6 см. Розріж його на 4 рівні частини і склади з них 2 квадрати.
12. Побудуй прямокутник зі сторонами 9 см і 4 см. Розріж його по ламаній лінії на такі дві частини, щоб можна було скласти квадрат.
13. Є бідони на 5 л і 3 л. Треба з цистерни відлити 7 л молока. Як це зробити?
14. Є два пакети. Один вміщує 200 г цукрового піску, а інший — 350 г. Як за допомогою цих пакетів відсипати 500 г цукру?
4 клас
1. Запиши різними цифрами найбільше п'ятицифрове число, в якого сума цифр дорівнює 10.
2. У числі 59 241 закресли такі дві цифри, щоб число, утворене залишеними цифрами, було: а) найбільшим; б) найменшим.
3. В яких з даних рівнянь значення невідомого однакові? 314
Розділ XV. Позакласна робота з математики
600 - (х + 20) = 200 600 - х + 20 = 200
(600 - 20) - х = 200 600 - х - 20 = 200
4. Віднови цифри:
х2х
х5
111
5. Два хлопчики зі швидкістю 80 м/хв вийшли назустріч один одному. Відстань між ними була 960 м. З одним хлопчиком був собака, який біг у 4 рази швидше, ніж ішов хлопчик. Собака бігав від одного хлопчика до іншого, а потім назад. Скільки метрів пробіг собака, поки хлопчики йшли назустріч один одному?
6. Швидкість течії річки дорівнює 5 км/год. Катер проплив за течією річки 180 км за 6 год, а потім ту саму відстань у зворотному напрямі. Скільки годин катер плив проти течії?
7. З ділянки площею 4 а зібрали 3 400 кг буряків, з ділянки площею 5а — 4 800 кг і з ділянки площею 6 а — 5 300 кг. Визнач середню врожайність буряків з одного ара всієї засіяної площі.
8. За 6 год молодий робітник обробляє 192 деталі. Його наставник за одну годину обробляє на 8 деталей більше, ніж молодий робітник. За скільки годин наставник обробить 320 деталей?
9. Задача з оповідання А.П. Чехова. "Купець купив 138 аршинів чорного і синього ■.сукна за 540 грн. Запитується, скільки аршинів купив він першого і другого, якщо
синє сукно коштувало 5 грн. за аршин, а чорне — 3 грн.?".
10. Брат у 3 рази старший за сестру, а сестра на 6 років молодша, ніж брат. Скільки років кожному?
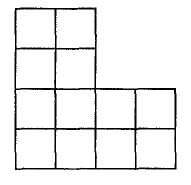
11. Фігура містить 12 квадратів. Розріж її на 4 однакові частини (мал. 174).
Мол. 174
12. Ставок має форму квадрата. Біля його вершин ростуть верби. Треба у 2 рази збільшити площу ставка, але так, щоб він мав форму квадрата і верби не опинилися у воді.
13. Запиши всі можливі трицифрові числа, які можна утворити з цифр 0, 1, 2 і 3. Повторювати цифри не можна.
14. Для зв'язку між кожними 2 артилерійськими батареями виділили одного зв'язківця. Скільки зв'язківців потрібно, щоб забезпечити зв'язок між 5 батареями?
РОЗДІЛ XVI
ВИХОВНА РОБОТА НА УРОЦІ МАТЕМАТИКИ
Молодший школяр відрізняється від дорослої дитини не тільки обсягом знань і умінь. Ця відмінність якісна: він про все робить висновок по-своєму, бачить, оцінює по-своєму, в нього інша логіка, а не просто "менш логічна", ніж у вчителя або батьків. І те нове, що відкривають дитині у школі, — це не "доважок", а кардинальна перебудова її досвіду, в результаті якої й з'являється новий, розумний погляд на світ.
Кожна країна зміцнюється і багатіє сумлінною та наполегливою працею своїх громадян, тому діти мають зрозуміти, що любов до Батьківщини має бути дієвою і корисними своїй країні мусять бути не тільки дорослі, а й діти. Однак найголовніше завдання школярів — вчитися.
Традиційно виховна діяльність в українській сім'ї зорієнтована на досягнення християнсько-національного виховного ідеалу. В центрі уваги батьків стояла і стоїть особистість дитини, її самоцінність. Головними засадами розвитку особистості є усталені моральні норми народу як частка загальнолюдських цінностей. Український менталітет і духовність грунтуються насамперед на гуманістичних принципах, моральних цінностях, в основі яких лежать прагнення гармонії з природою, християнські чесноти.
Виховання — це сукупність знань, культурних навичок, поглядів, що становлять загальний рівень духовного розвитку дитини і є результатом систематичного впливу навчання; це сума впливів на психіку людини, спрямованих на підготовку її до активної участі у виробничому, громадському й культурному житті суспільства. Виховання досягає великих успіхів, якщо враховують його залежність не тільки від віку, а й від індивідуальних особливостей розвитку дитини.
Об'єктивне та систематичне оцінювання навчальної, суспільно корисної діяльності і поведінки молодших школярів учителем, однокласниками і батьками сприяє розвитку в них самосвідомості і пов'язаних з нею таких рис, як відповідальність, почуття власної гідності, повага до іншої людини.
У початкових класах закладаються основи охайності, точності, чемності, вміння поводитись у школі, на вулиці, в громадських місцях.
Молодші школярі мають добре усвідомити, що основна риса вихованої людини — це повага до інших. Без цього гарні зовнішні прояви культури будуть фальшиві й лицемірні.
Виховання гуманних якостей — важливе завдання вчителів і батьків. Доброта, чуйність, турботливість, уважність, дієва любов до всього живого — засади гуманізму та милосердя. Виховуючи в дитини спрямованість на іншу людину, формуючи ставлення до оточення як до цінності, не меншої, ніж цінність власної особистості, ми закладаємо в дитячій душі основи для розвитку найкращих людських якостей.
316
РозділXVI. Виховна робота на уроці математики
Особливість і відповідальність початкової школи у вихованні дітей полягають у тому, що перші симптоми неправильного формування особистості виявляються вже в молодшому шкільному віці. Учитель має своєчасно помітити це і вжити заходів щодо усунення причин, які призвели до похибок у вихованні.
На уроках математики здійснюється як вузькопрофесійне, так і комплексне виховання.
Вузькопрофесійне виховання забезпечує розвиток специфічних якостей математичної діяльності (точність, логічність у судженнях, кмітливість), зв'язок з практикою при введенні понять і розв'язуванні задач.
Комплексне виховання передбачає формування не тільки професійно-математичних якостей учня. Воно відповідає принципу всебічного й гармонійного розвитку особистості. Адже виховний процес неперервний. На виховних заняттях нерідко узагальнюються знання, нагромаджені на уроках, у групі продовженого дня, у позакласній роботі.
У початкових класах виховання на уроках математики здійснюється значною мірою на основі розв'язування задач. Задачі дають змогу пов'язувати навчання з життям, ознайомлювати учнів з пізнавально важливими фактами.