экономика. ДИПЛОМ Чадан. Общая характеристика района
 Скачать 3.68 Mb. Скачать 3.68 Mb.
|
|
2.3.2 Определение сил сопротивления движения ленты Силы сопротивления на ленточном конвейере разделяются на статические, не зависящие от ускорения ленты, и динамические. Статические силы сопротивления на ленточном конвейере разделяют на распределенные (которые распределены на значительной длине) и сосредоточенные (силы сопротивления в местах погрузки, на отклоняющих барабанах, силы сопротивления очистных устройств и т.д.). Динамические силы сопротивления проявляются при пуске и остановке конвейера, зависят от его конструктивных особенностей и ряда режимных параметров и в приближенных расчетах учитываются увеличением запаса прочности ленты. Силы сопротивления грузовой и порожней ветвей с учетом сопротивления вращающихся частей роликоопор: -для порожняковой ветви 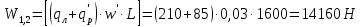 (2.3.2.1) (2.3.2.1) 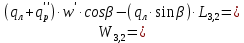 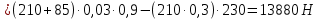 (2.3.2.2) (2.3.2.2) 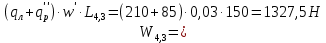 (2.3.2.3) (2.3.2.3)-для грузовой ветви 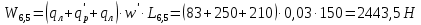 (2.3.2.4) (2.3.2.4)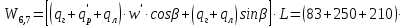 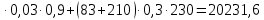 Н (2.3.2.5) Н (2.3.2.5)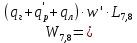 =(83+250+210) ∙ 0,03 ∙ 1600 = 26064 Н (2.3.2.6) =(83+250+210) ∙ 0,03 ∙ 1600 = 26064 Н (2.3.2.6)где 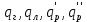 - распределенная линейная нагрузка соответственно от груза, ленты, вращающихся частей роликоопор верхней и нижней ветвей, Н/м; - распределенная линейная нагрузка соответственно от груза, ленты, вращающихся частей роликоопор верхней и нижней ветвей, Н/м;  - коэффициент сопротивления движению для грузовой и порожней ветвей, равный 0,03; L- длина рассматриваемого участка, м. - коэффициент сопротивления движению для грузовой и порожней ветвей, равный 0,03; L- длина рассматриваемого участка, м.Распределенная линейная нагрузка от массы транспортируемого груза 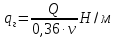 , (2.3.2.7) , (2.3.2.7)где Q – производительность конвейера, т/ч. 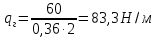 . .2.3.3 Тяговый расчет конвейера Полное сопротивление движению конвейерной ленты определяется методом обхода контура конвейера. Для этого весь контур конвейера разбивают на участки (рис.2.3.3.1), границы которых обозначают характерными точками. Эти точки вводятся в тех местах, где изменяются характеристики трассы: угол наклона конвейера, появляется сосредоточенное сопротивление и т.п. 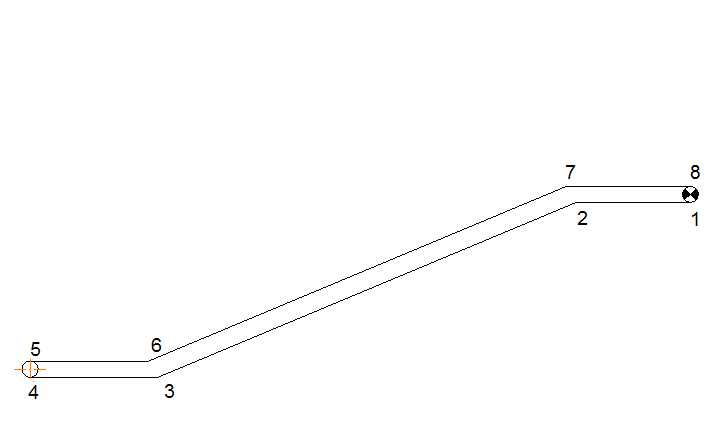 Рис.2.3.3.1. Расчетная схема конвейера Пронумеровав все точки контура, находим натяжения в них по формулам: 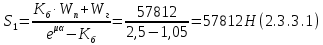 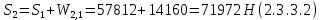 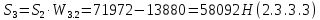 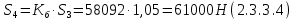 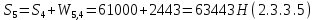 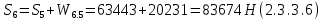 Определяем тяговое усилие по формуле: 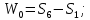 (2.3.3.7) (2.3.3.7)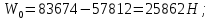 но фактическое тяговое усилие будет больше на 2%, так как при расчетах не учитывалось сопротивления на отклоняющих барабанах натяжной станции. Таким образом, тяговое усилие 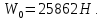 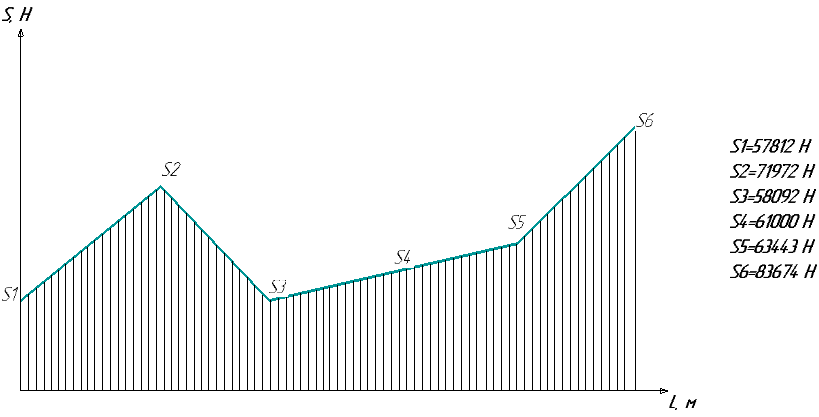 Рис. 2.3.3.2. Натяжение ленты в характерных точках контура конвейера. 2.3.4 Выбор ленты конвейера Принимаем к установке резинотканевую ленту. Для резинотканевых лент определяют число прокладок по выбранной прочности прокладки, т.е. по σр в Н на 1 мм ширины одной прокладки ленты: 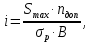 (2.3.4.1) (2.3.4.1)где 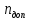 – запас прочности ленты; – запас прочности ленты;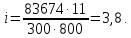 Число прокладок принимаем равным 4. Выбираем резинотканевую ленту марки ТЛК-300, у которой σр=1200 Н/мм – разрывное усилие, отнесенное к 1мм ширины ленты, mл=14,2 кг – масса 1м2 ленты, L=800 мм. 2.3.5 Определение мощности привода Мощность приводной станции N (кВт) определяется по формуле: 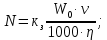 (2.3.5.1) (2.3.5.1)где η=0,85÷0,9 – КПД механической передачи, 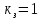 - коэффициент запаса мощности. - коэффициент запаса мощности.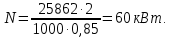 2.4 Расчет динамических нагрузок в канатах става ленточного конвейера Часто на ленточных конвейерах с канатным ставом подвесные роликоопоры мест загрузки крепятся непосредственно к несущим канатам, которые являются хорошими амортизаторами, обладающими к тому же нелинейными характеристиками. В этом случае канаты необходимо рассчитывать на суммарные статические и динамические нагрузки. Для расчета динамических нагрузок канаты става заменим упругой гибкой нитью с параметрами, равными суммарным параметрам канатов. Для вывода основных соотношений первоначально проанализируем деформации упругой нити жестко закрепленной в точках подвески с сосредоточенной массой посредине (рис.2.4.1, а); при этом погонной массой нити по сравнению с сосредоточенной массой пренебрегаем. 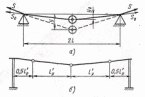 Рис 2.4.1. К расчету динамических усилий в канатах става (жестко закрепленных на стойках): а – для одной, б – для трех масс в пролете. Введем следующие обозначения: m – сосредоточенная масса; y0 – начальное статическое смещение массы m; y – суммарное (динамическое и статическое) смещение нити; F, FK – площадь поперечного сечения нити и каната (F=2FK); E – модуль упругости материала нити; l – половина расстояния между точками закрепления. Сила растяжения нити S равна 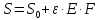 . (2.4.1) . (2.4.1)Относительное удлинение нити ɛ, соответствующее ее вертикальному смещению на величину y, равно 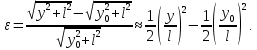 (2.4.2) (2.4.2)Восстанавливающую силу определим как 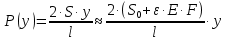 (2.4.3) (2.4.3)Членом y02/l2 в уравнении (2.4.2) пренебрегаем, так как он – величина второго порядка малости; тогда уравнение (2.4.3) можно преобразовать к виду 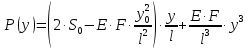 . .Рассмотрим процесс удара куска массой M по массе m, закрепленной на нити; скорость куска в момент удара равна υ. При решении задачи воспользуемся законом сохранения энергии. Потенциальная энергия системы состоит из двух частей: потенциальной энергии деформации растянутой нити и потенциальной энергии массы m, зависящей от ее положения. Следовательно, кинетическая энергия T0, приобретенная массой m, равна потенциальной энергии нити при ее максимальном отклонении за вычетом начальной потенциальной энергии: 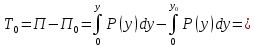 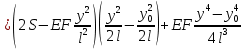 . (2.4.4) . (2.4.4)Из выражения (2.4.4) получим 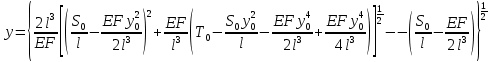 . (2.4.5) . (2.4.5)Подставляя в выражение (2.4.1) значение y из (2.4.5), получим 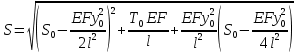 . (2.4.6) . (2.4.6)Определим кинетическую энергию T0, сообщенную массе m. Если удар не абсолютно упругий и коэффициент восстановления равен μ, то начальную скорость массы m (м/с) определяем как 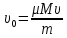 , , и следовательно, 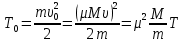 , (2.4.7) , (2.4.7) где T – кинетическая энергия падающего куска. Таким образом, для схемы, изображенной на рис.2.4.1, а, задача решена. При ударе куска груза по средней роликоопоре практически одновременно с ней начнут перемещаться и боковые роликоопоры. Исходя из геометрических соображений, имеем приближенное соотношение 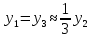 , (2.4.8) , (2.4.8)отсюда 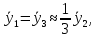 где 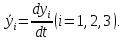 Полная кинетическая энергия системы 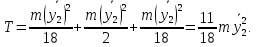 Отсюда приведенная масса, участвующая в ударе, равна 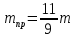 ; это значение необходимо использовать при определении T0 по уравнению (2.4.7): ; это значение необходимо использовать при определении T0 по уравнению (2.4.7):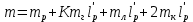 , (2.4.9) , (2.4.9)где mр – масса роликоопоры; mг, mл, mк – погонная масса груза, ленты и канатов; K – коэффициент, учитывающий количество груза, приходящегося на каждую роликоопору в месте погрузки (K изменяется от 1 до 0). Выражение (2.4.6) применимо, в случае если канаты жестко закреплены на стойках и жесткость стоек значительна. Однако если погрузка осуществляется в средней части конвейера с канатами, свободно опирающимися на стойки, то при решении необходимо учитывать податливость соседних участков. При этом возможны два случая (рис.2.4.2). 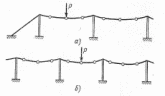 Рис 2.4.2. К расчету динамических усилий в канатах става: а – с одной упругой заделкой, б – с двумя упругими заделками. Рассмотрим определение динамического усилия для случая, изображенного на рис.2.4.2, а. Относительное удлинение каната определяется как разность между полной деформацией системы и деформацией пружины с податливостью, эквивалентной податливости соседнего участка става. Согласно уравнению (2.4.2) запишем 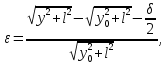 (2.4.10) (2.4.10) где δ – деформация пружины, равная 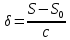 ; с – жесткость пружины. ; с – жесткость пружины. В выражении (2.4.10) предполагается, что суммарная деформация пружины δ делится пополам между отрезками l. Преобразовав выражение (2.4.10), получим следующие выражения для относительной деформации: 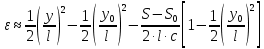 и натяжение каната по (2.3.1) равно 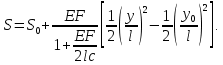 (2.4.11) (2.4.11)Сравнив уравнение (2.4.11) с уравнением (2.4.1) видим, что вместо величины EF для случая жесткого закрепления канатов в данном случае необходимо использовать величину 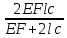 . Аналогично для схемы, изображенной на рис.2.4.2,б и соответствующей загрузке в средней части конвейера, получим . Аналогично для схемы, изображенной на рис.2.4.2,б и соответствующей загрузке в средней части конвейера, получим 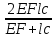 . .Для определения динамических усилий необходимо в соответствии с конструкцией конвейера определить жесткость соседних участков катанного става. С достаточной для практических расчетов точностью считаем, что при ударе деформируется по одному пролету с каждой стороны. Пусть из соседнего пролета при ударе выбирается часть каната длиной δ при возрастании натяжения каната в нем на величину S – S0 – Fтр, где S – S0 увеличение натяжения каната в пролете, в котором произошел удар, а Fтр – сила трения каната о стойку. Таким образом, среднюю жесткость соседнего пролета можно определить как c = (S – S0 – Fтр)/δ. Если другой конец каната в соседнем пролете считать жестко закрепленным, то изменение длины каната в этом пролете 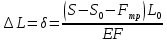 , (2.4.12) , (2.4.12)где L0 – начальная длина каната в пролете 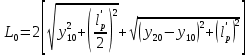 ; ;yi0 – значение провесов при натяжении S0. Изменение длины каната в пролете 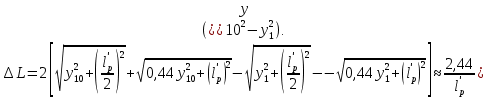 Подставляя выражения для L0 и ∆L в (2.4.12) и пренебрегая величиной 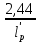 , получим , получим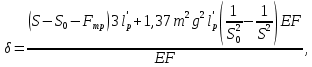 и жесткость пролета при навеске трех роликоопор 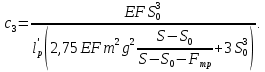 (2.4.13) (2.4.13)Сила трения Fтр невелика по сравнению с величиной S – S0, поэтому ею можно пренебречь. Расчеты: Исходные данные: Производительность Q=60 т/ч; Ширина ленты B=800 мм; Скорость ленты 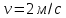 . .Статическое натяжение для двух канатов при навеске трех роликоопор между стойками равно S0 = 6000 Н. Определим эквивалентную сосредоточенную массу по формуле (2.4.9) m = 240 + 83,3∙0,8 + 210∙0,8 + 2∙80∙0,8 = 602,64 Н, откуда приведенная масса по (2.3.9) 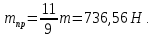 Определим кинетическую энергию T0 по формуле (2.4.7). Для расчета принимаем: масса куска падающего на ленту М=10 кг; высота падения груза h=0,5 м; коэффициент восстановления, определяемый экспериментально, μ=0,5; квадрат скорости падения куска υ2 =2gh=10 м2/с2. Подставляя эти значения в выражение для T0, получим: 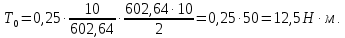 Жесткость соседнего пролета при навеске в нем трех роликоопор определим по формуле (2.4.13), пренебрегая силой трения: 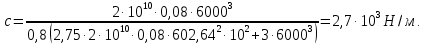 По формуле (2.4.11) определим динамические условия, возникающие в канатах става при погрузке в хвостовой части конвейера: 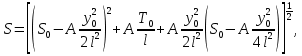 где 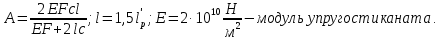 Подставляя значения всех величин, получим 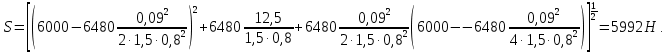 2.5 Условие эксплуатации ленточных конвейеров Увеличение производительности очистных забоев за счет внедрения новых средств механизации, влечет за собой развитие наиболее прогрессивных поточных видов транспорта, основу которого составляют ленточные конвейеры, обеспечивающие рост производительности труда и снижение себестоимости транспортирования полезного ископаемого. В связи с этим совершенствование их конструкций и улучшение технико-экономических показателей является основной задачей, стоящей перед конвейерным транспортом. Около 70% процентов всех ленточных конвейеров транспортируют горную массу, крупность кусков которой зачастую превышает 200 мм. Падение таких крупных кусков на ленту, а также их транспортирование, может привести к пробоям ленты и выходу из строя подшипниковых узлов роликов. Большинство ленточных конвейеров оснащены главным образом жесткими трехроликовыми опорами, поддерживающими груженую ветвь и однороликовыми – для порожняковой ветви конвейера. Установлено, что на каждом конвейере имеется определенный процент невращающихся роликов, причем причём одной из главных причин преждевременного выхода из строя роликов груженной ветви ленточных конвейеров являются значительные динамические нагрузки, возникающие в подшипниковых узлах при транспортировании крупнокусковых грузов. Для повышения срока службы конвейерных лент при транспортировании горной массы особое значение имеет правильное устройство пунктов загрузки. В настоящее время, в пунктах загрузки ленточных конвейеров преимущественно устанавливают жесткие роликоопоры, такие же, как и на линейных секциях. На некоторых конвейерах применяют обрезиненные ролики, работа которых малоэффективна. С целью уменьшения контактных нагрузок на ленту и ролики, возникающих в процессе погрузки на ленточный конвейер горной массы, иногда устанавливают колосниковые решетки, обеспечивающие подсев мелких фракций породы для образования на ленте «постели». Известно, что контактная динамическая нагрузка на ленту и роликоопоры узлов загрузки зависит от высоты падения кусков груза, которая колеблется в пределах от 0,2 до 2,0 м. Анализ условий эксплуатации ленточных конвейеров показывает, что их отдельные узлы требуют изменения. Широкое применение в горнодобывающей промышленности ленточных конвейеров, способных транспортировать полезные ископаемые на большие расстояния и с минимальными затратами, предъявляет высокое требование надежности и долговечности конвейера в целом, а также отдельных его узлов. С увеличением длины транспортирования существенно возрастает стоимость конвейерной ленты и роликов, составляющих большую часть стоимости конвейерной установки, так как является основными массовыми узлами ленточных конвейеров. Создание конструкций роликов, не требующих периодического возобновления смазки, применение современных видов уплотнений подшипниковых узлов и долговременной смазки позволит создать роликоопоры, работающие без ремонта и дополнительной смазки не менее 3 лет. |
