экономика. ДИПЛОМ Чадан. Общая характеристика района
 Скачать 3.68 Mb.
|
|
4.1.2. Расчет и построение механических характеристик асинхронного двигателя в тормозных режимах. В упрощенном варианте механическая характеристика в режиме динамического торможения является зеркальноотображенной относительно начала координат и смещенной вверх в начало координат. Эта характеристика представлена на рис.4.1.2. Значения добавочных сопротивлений принимаем равными сопротивлениям в двигательном режиме. Торможение двигателя начинается со скорости wC = 103.38 c-1. 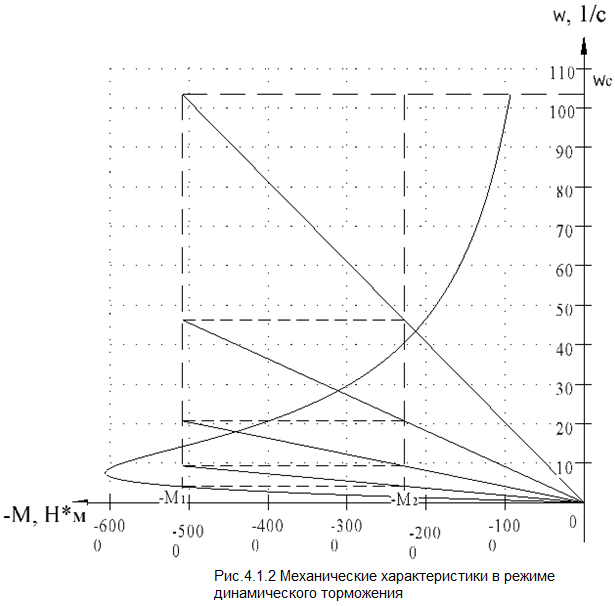 4.2. Расчет и построение механических переходных процессов 4.2.1. Расчет механических переходных процессов в двигательном режиме Расчет переходных процессов с линейными механическими характеристиками двигателя ведется по формулам: для угловой скорости 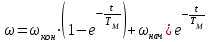 ; (4.2.1)для момента 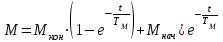 , (4.2.2)где wнач, wкон – соответственно начальная и конечная угловые скорости двигателя; Mнач, Mкон – соответственно начальный и конечный моменты двигателя; TM – механическая постоянная времени элекропривода. Произведем расчет механического переходного процесса при пуске привода с линейной механической (в рабочей части) характеристикой двигателя и постоянным моментом сопротивления рабочей машины. Рассмотрим пуск двигателя в четыре ступени. Работа двигателя на первой ступени описывается выражением, полученным из уравнения (4.2.1), в котором принимают wнач = 0. Тогда 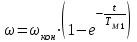 , (4.2.3)где wкон – конечная угловая скорость двигателя, работающего на первой ступени пускового резистора; TM1 – механическая постоянная времени, соответствующая работе привода на первой ступени пускового резистора: для асинхронного двигателя 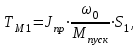 (4.2.4)где Jпр – момент инерции электропривода, приведенный к валу двигателя; S1 – скольжение АД на искусственной механической характеристике, соответствующего номинальному моменту. Механическая постоянная времени: для асинхронного двигателя, работающего на естественной механической характеристике  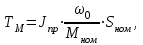 (4.2.5)Тогда 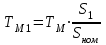 - для асинхронного двигателя, где S1 – скольжение АД на искусственной механической характеристике, соответствующего номинальному моменту.Конечная угловая скорость на первой ступени wкон = wс1. Работа двигателя на первой пусковой ступени длится (34)TM1. Задаваясь временем от t = 0 до t = 4TM1, определяем угловую скорость двигателя и результаты расчетов сводим в табл.4.2.1. По данным табл.4.2.1. строим кривую зависимости угловой скорости от времени w = f(t), которая приведена на рис.4.2.1. 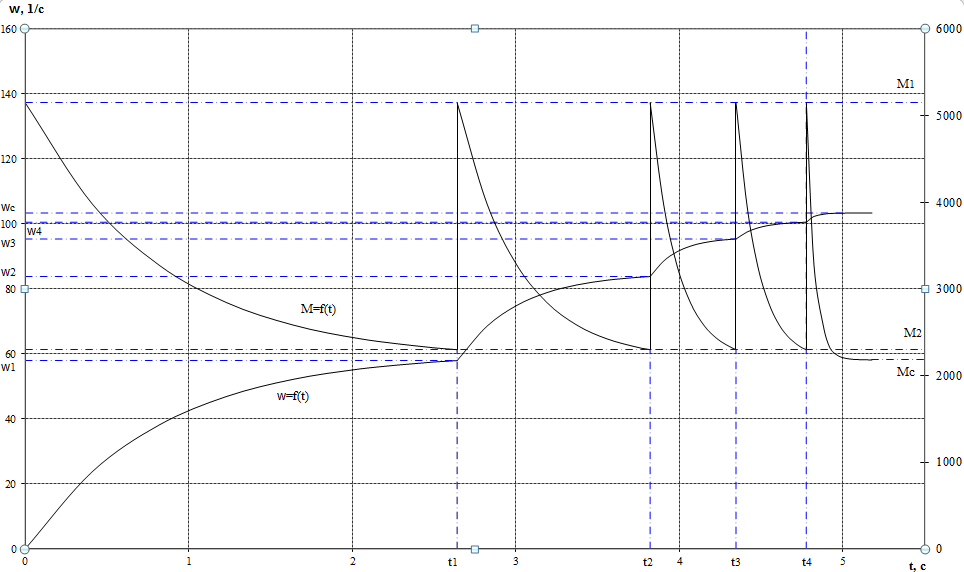 Рис.4.2.1 Кривые переходного процесса при пуске двигателя Однако при реализации автоматического управления пуском, двигателя разгоняется лишь до скорости w1, так как при этой скорости происходит переход двигателя на новую механическую характеристику. Поэтому для определения времени работы на первой ступени из уравнения (4.2.1) получим формулу для определения времени работы на ступени 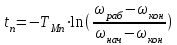 , (4.2.6)где tn – время работы на n-ной ступени; TMn – постоянная времени n-ной ступени; 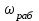 - угловая скорость, при которой происходит переключение;Далее расчет зависимости w = f(t) ведется по формуле (4.2.1), в которой начальными и конечными условиями будут wнач = w1, wкон = wс2. Механическая постоянная времени электропривода 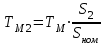 , где S2 – берется из графика на рис.4.1.1. (4.2.7)Аналогично предыдущему задаемся временем t и рассчитываем w, а результаты сводят в табл.4.2.2, 4.2.3, 4.2.4, 4.2.5 соответственно и строим переходный процесс, приведенный на рис.4.2.1. Таблица 4.2.1.
Таблица 4.2.2.
Таблица 4.2.3.
Таблица 4.2.4.
Таблица 4.2.5.
Данные времен работы двигателя на ступенях и постоянные времени представлены в табл.4.2.6. и табл.4.2.7. соответственно. Таблица 4.2.6. Таблица 4.2.7.
Расчет зависимости M=f(t) ведут по формуле (4.2.2), в которой начальные и конечные значения Mнач = M1, Мкон = Мс одинаковы для всех ступеней пускового резистора, а изменяется лишь величина механической постоянной времени. Для первой ступени TM = TM1, для второй ступени TM = TM2 и т.д. Задаваясь временем t с теми же значениями, что и при расчете кривой w=f(t), находят момент М, а результаты расчетов занесем в табл.4.2.1…4.2.5. По данным этих таблиц построена криваяM=f(t), которая представлена на рис.4.2.1. 4.2.2. Расчет механических переходных процессов двигателя, работающего в режиме динамического торможения. Рассмотрим механический переходный процесс при динамическом торможении двигателя. Расчет механического переходного процесса при торможении двигателя ведется по формуле: 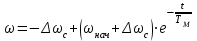 , (4.2.8)в которой Dwc – перепад скорости при моменте нагрузки Мс, а также начальная скорость wнач. Величины wнач и Dwc берутся из графика, изображенного на рис.4.2.2 и представленного ниже. Расчет переходного процесса ведется по формуле (4.2.8) до скорости w = -wc. Задаваясь временем t от 0 до 4TM1. Результаты расчета занесем в табл.4.2.8, по которым построим зависимость w = f(t) представленную на рис.4.2.3. Аналогично расчету переходного процесса для двигательного режима занесем данные расчетов в табл.4.2.8, 4.2.9, 4.2.10, 4.2.11, 4.2.12 соответственно. Расчет зависимости M=f(t) при торможении двигателя в режиме динамического торможения ведется по формуле (4.2.2), в которой Mнач = -M1, Мкон = Мс. Таблица 4.2.8.
Таблица 4.2.9.
Таблица 4.2.10.
Таблица 4.2.11.
Таблица 4.2.12.
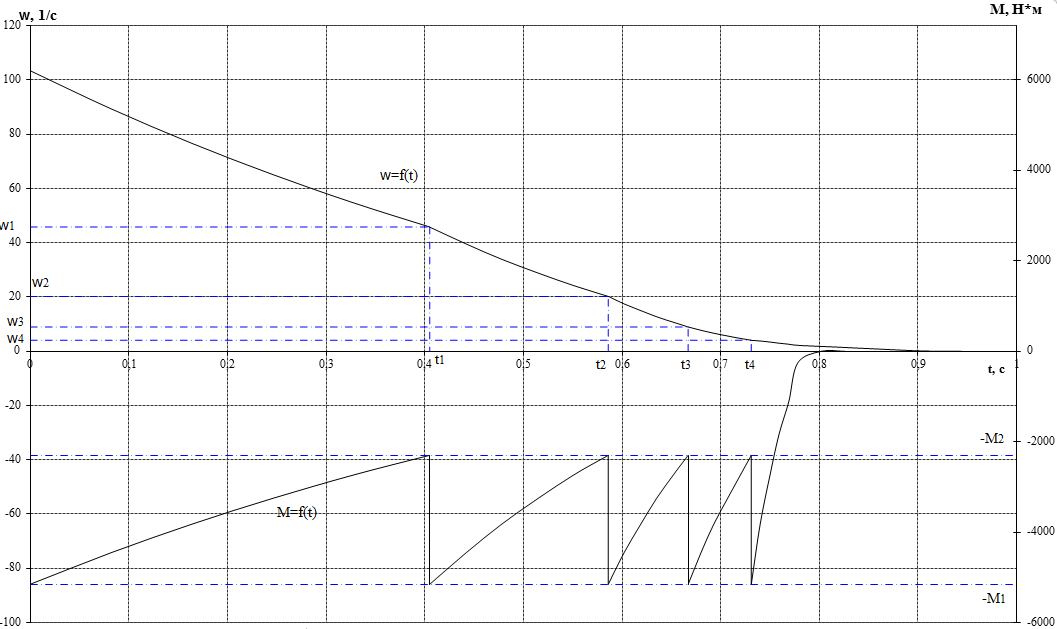 Рис.4.2.3 Кривые переходного процесса в режиме динамического торможения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||