§ 3.3. Способы изменения скорости
простых и сложных реакций
Как указывалось, скорость химической реакции зависит от большого числа различных факторов. Из кинетических уравнений следует, прежде всего, что скорость простой реакции пропорциональна концентрациям веществ, являющихся реагентами в данной реакции. Следовательно, для простых реакций увеличение концентрации исходных веществ практически всегда приводит к увеличению скорости (за исключением реакций нулевого порядка, скорость которых не зависит от концентрации).
Если реакция, описываемая стехиометрическим уравнением (I), характеризуется различающимися частными порядками по компонентам А и В, наибольшее влияние на скорость реакции будет оказывать изменение концентрации реагента, имеющего больший частный порядок. Например, если кинетическое уравнение реакции, в которой участвуют два реагента, имеет вид 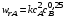 , то увеличение концентрации реагента А в 2 раза вызовет рост скорости в 4 раза, а двукратное повышение концентрации реагента В приведет к возрастанию скорости лишь в 1,19 раза. , то увеличение концентрации реагента А в 2 раза вызовет рост скорости в 4 раза, а двукратное повышение концентрации реагента В приведет к возрастанию скорости лишь в 1,19 раза.
Для сложных реакций, в частности для параллельных, вопрос о выборе концентраций реагентов для управления процессом также не является однозначным. Рассмотрим для примера систему из двух параллельных реакций разного порядка (при постоянной температуре):
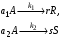 (II) (II)
Говоря об увеличении скорости такой реакции, нужно сначала решить, какая реакция более важна, т. е. какая реакция приводит к образованию нужного целевого продукта. Нас интересует чаще всего не то, насколько быстро израсходуется реагент А, а насколько быстрее будет образовываться целевой продукт по сравнению с побочным.
Пусть в рассматриваемом примере целевым является продукт первой реакции R, а побочным – продукт S.
Для анализа соотношения скоростей целевого и побочных процессов пользуются мгновенной, или дифференциальной, селективностью, равной отношению скорости расходования реагента А на целевую реакцию к общей скорости расходования реагента и на целевую, и на побочные реакции.
Значение дифференциальной селективности в ходе процесса в общем случае не остается постоянным, так как оно определяется отношением скоростей реакций, а скорость реакции по мере ее протекания меняется. Таким образом, дифференциальная селективность характеризует эффективность целевой реакции в некоторый момент времени при некотором значении концентраций реагентов и продуктов и при заданной температуре. Лишь в том случае, когда параметры процесса во времени и пространстве не меняются (это возможно при проведении процесса в стационарном реакторе идеального смешения), φ' остается постоянной величиной.
При протекании химической реакции меняются концентрации реагентов и продуктов. Рассмотрим, как при изменении концентрации исходного реагента А для системы параллельных реакций (II) при постоянной температуре процесса меняется дифференциальная селективность φ'.
Пусть целевая реакция имеет по исходному реагенту А порядок n1, а побочная реакция – п2,тогда
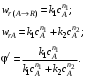 (3.5) (3.5)
Проанализируем зависимость φ' от концентрации реагента А. Для удобства преобразуем выражение (3.5):
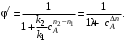 (3.6) (3.6)
Здесь 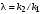 t– величина, не зависящая от концентрации реагента A; n = п2 – п1– разность порядков побочной и целевой реакций по исходному реагенту А. t– величина, не зависящая от концентрации реагента A; n = п2 – п1– разность порядков побочной и целевой реакций по исходному реагенту А.
Очевидно, что φ' может быть как возрастающей, так и убывающей функцией от концентрации. Определим характер функции φ'(сА) по знаку первой производной:
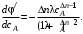 (3.7) (3.7)
Как видно из уравнения (3.7), знак первой производной зависит от знака 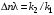 – всегда положительного, сA в любой степени также положительная величина. Если ∆n < 0, т. е. если n1 > п2(порядок целевой реакции по исходному реагенту больше порядка побочной реакции), то φ'(са) – возрастающая функция; скорость целевой реакции с ростом концентрации исходного реагента возрастает значительно быстрее скорости побочной реакции и доля скорости целевой реакции в суммарной скорости возрастает (рис. 3.1, кривая 2). – всегда положительного, сA в любой степени также положительная величина. Если ∆n < 0, т. е. если n1 > п2(порядок целевой реакции по исходному реагенту больше порядка побочной реакции), то φ'(са) – возрастающая функция; скорость целевой реакции с ростом концентрации исходного реагента возрастает значительно быстрее скорости побочной реакции и доля скорости целевой реакции в суммарной скорости возрастает (рис. 3.1, кривая 2).
В этом случае желаемый результат – увеличение скорости образования целевого продукта R по сравнению со скоростью образования побочного продукта S (увеличение дифференциальной селективности φ') – достигается при использовании исходного реагента высокой концентрации.
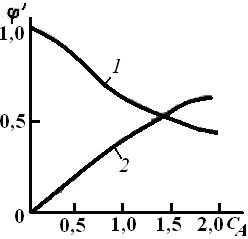
Рис. 3.1. Зависимость дифференциальной селективности от концентрации исходного реагента А для параллельных реакций при различных соотношениях порядков реакций n1 и п2: 1 – п1= 1, k1 = 10 ч–1 n2 = 2,5, k2 = 15 м4,5/(кмолъ1,5·ч);
2 – n1 = 2,5, k1 =154,5/(кмолъ1,5·ч); n2 = 1; k2 = 10 ч–1
При ∆n > 0 (n1 < п2)характер зависимости φ' от концентрации исходного реагента противоположный: dφ'/dcA < 0, следовательно, φ'(сА) – убывающая функция (кривая 1),и более высокая дифференциальная селективность по целевому продукту достигается при низкой концентрации исходного реагента. Следовательно, не всегда выгодно стремиться увеличивать концентрацию реагента. Правда, при низких концентрациях реагента небольшим будет абсолютное значение скорости при прочих равных условиях. Тогда нужно искать другие пути увеличения скорости реакции при сохранении высокого значения дифференциальной селективности. При ∆n = 0 дифференциальная селективность, как это видно из уравнения (3.7), остается постоянной величиной при любых значениях концентрации исходных реагентов, и изменить φ' можно, лишь изменив соотношение k2/k1.
Проще всего можно повлиять на это соотношение, изменив температуру проведения реакции, так как температура является одним из технологических параметров, в наибольшей степени влияющим на скорость химической реакции. Рассмотрим влияние температуры на скорость химической реакции более подробно.
Экспериментально при изучении кинетики химических реакций было обнаружено, что при увеличении температуры на 10 градусов скорость реакции возрастает в 2–4 раза. Более строго эта зависимость выражается в виде уравнения Аррениуса
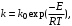 (3.8) (3.8)
где k – константа скорости реакции; k0– предэкспоненциальный множитель; Е – энергия активации реакции; R – универсальная газовая постоянная; Т – температура.
Энергия активации элементарной реакции Е – это минимальный избыток энергии над средней внутренней энергией молекул, необходимый для того, чтобы произошло химическое взаимодействие (энергетический барьер, который должны преодолеть молекулы при переходе из одного состояния реакционной системы в другое).
Для обратимых реакций разность энергий активации прямой (E1) и обратной (Е2)реакций равна тепловому эффекту реакции.
Предэкспоненциальный множитель k0 учитывает число соударений, вероятность распада активированного комплекса реакции на исходные реагенты без образования продуктов реакции, пространственную ориентацию молекул реагентов, а также ряд других факторов, влияющих на скорость реакции и не зависящих от температуры. При более строгом рассмотрении следует учесть, что k0также зависит от температуры, но при температурах, когда RT<<Е,с достаточно хорошим приближением этой зависимостью можно пренебречь.
Часто уравнение Аррениуса представляют в виде линейной зависимости логарифма константы скорости от обратной температуры: ln k = f(l/T). В таком виде удобно провести его анализ.
Из анализа зависимости ln k = f(l/T),приведенной на рис. 3.2, можно сделать следующие выводы.
Во-первых, из неравномерности температурной шкалы следует, что химические реакции более чувствительны к изменениям температуры в области более низких температур. На прямой 1,соответствующей химической реакции с энергией активации 165 кДж/моль, выбраны два участка I и II, характеризующиеся одинаковым изменением температуры (∆T = 100 К), но в разных температурных интервалах: участок I – в области температур, близких к комнатной температуре, участок II – в области более высоких температур (
600 К). Для участка I при изменении температуры на 100 градусов константа скорости реакции k1увеличивается в 1,9·107 раз, для участка II при той же ∆T наблюдается увеличение константы скорости лишь в 820 раз, примерно на четыре порядка ниже, чем на участке I.
Второй важный вывод вытекает из сравнения температурных зависимостей скоростей реакций с различными значениями энергии активации. Чем выше энергия активации реакции, тем более чувствительна она к изменениям температуры.
При изменении температуры от 500 до 600 К скорость первой реакции (Е = 165 кДж/моль) увеличивается в 820 раз (участок II), а скорость второй реакции (E = 40 кДж/моль) – лишь в 5,3 раза (участок III).
Последний вывод чрезвычайно важен при выборе условий проведения сложных (параллельных и последовательных) реакций.
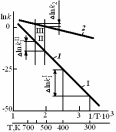
Рис. 3.2. Зависимость константы скорости химической реакции от температуры для реакций с энергиями активации 165 кДж/моль (1) и 40 кДж/моль (2): участок I – изменение ln kпри росте температуры с 300 до 400 К; участок II – то же, при росте температуры с 500 до 600 К; участок III – изменение ln kдля реакции с низкой энергией активации при изменении температуры с 500 до 600 К
Рассмотрим, например, влияние температуры на дифференциальную селективность для параллельных реакций (II):
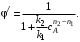
Для того чтобы выделить только влияние температуры на селективность, примем, что целевая и побочная реакции имеют одинаковый порядок (n1= п2). Преобразуем уравнение (3.6) с учетом уравнения (3.8):
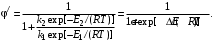
Пренебрегая слабым влиянием температуры на предэкспоненциальные множители в уравнении Аррениуса, считаем, что σ= k2,0/k1,0 от температуры не зависит. Производная положительна, если ∆Е=Е1–Е2>0, и отрицательна, если ∆Е < 0:
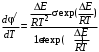 . .
Таким образом, если энергия активации целевой реакции превышает энергию активации побочной реакции, то с ростом температуры наблюдается возрастание дифференциальной селективности, т. е. относительно более быстрое увеличение скорости целевой реакции по сравнению с ростом скорости побочной реакции и суммарной скорости процесса. Наоборот, если E1 < Е2,для увеличения дифференциальной селективности φ' нужно понижать, а не повышать температуру.
Из уравнения Аррениуса видно, что принципиально возможен еще один путь управления скоростью химической реакции – изменение величины Е – энергии активации реакции. Высота энергетического барьера реакции тесно связана с ее механизмом. Если изменить путь реакции, направив ее к конечным продуктам через некоторые новые промежуточные комплексы, то можно изменить и значение энергии активации. Такой путь возможен при применении катализаторов.
Из приведенного выше рассмотрения влияния температуры на скорость реакции с различной энергией активации следует, что в случае применения катализатора для ускорения целевого процесса при проведении параллельных реакций, возможна такая ситуация, когда энергия активации побочной реакции окажется выше энергии активации целевой реакции. Тогда повышение температуры, часто применяемое для интенсификации химико-технологических процессов, приведет к снижению селективности по целевому продукту.
|
 Скачать 1.75 Mb.
Скачать 1.75 Mb.
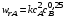
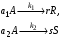 (II)
(II)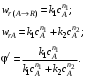 (3.5)
(3.5)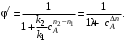 (3.6)
(3.6)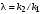
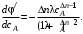 (3.7)
(3.7)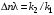 – всегда положительного, сA в любой степени также положительная величина. Если ∆n < 0, т. е. если n1 > п2(порядок целевой реакции по исходному реагенту больше порядка побочной реакции), то φ
– всегда положительного, сA в любой степени также положительная величина. Если ∆n < 0, т. е. если n1 > п2(порядок целевой реакции по исходному реагенту больше порядка побочной реакции), то φ
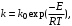 (3.8)
(3.8)
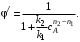
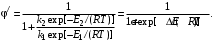
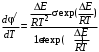 .
.