Общая химическая технология
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
§ 2.3. Зависимость константы равновесия от температурыФункциональная зависимость константы равновесия от температуры при постоянном давлении передается уравнением изобары Вант-Гоффа 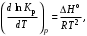 (2.9) (2.9)где ∆H° – изменение энтальпии при стандартном состоянии. Из уравнения (2.9) следует, что при положительных значениях ∆H° (эндотермические реакции) 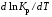 >0 и Кр(Т)– возрастающая функция. Если ∆H° < 0 (экзотермические реакции), то >0 и Кр(Т)– возрастающая функция. Если ∆H° < 0 (экзотермические реакции), то 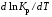 < 0 и константа равновесия уменьшается с повышением температуры. В обоих случаях равновесные концентрации участников реакции меняются, т. е. анализ уравнения показывает, что оно в количественной форме отражает вывод, вытекающий из принципа смещения равновесия: повышение температуры всегда смещает равновесие в направлении эндотермической реакции. < 0 и константа равновесия уменьшается с повышением температуры. В обоих случаях равновесные концентрации участников реакции меняются, т. е. анализ уравнения показывает, что оно в количественной форме отражает вывод, вытекающий из принципа смещения равновесия: повышение температуры всегда смещает равновесие в направлении эндотермической реакции.Для процессов, протекающих при постоянном объеме, зависимость константы равновесия от температуры передается уравнением изохоры Вант-Гоффа 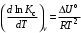 , ,где ∆U° – изменение внутренней энергии в стандартном состоянии. Уравнения изобары и изохоры реакции определяют зависимость константы равновесия от температуры в дифференциальной форме. Для практических расчетов равновесия при различных температурах требуется провести интегрирование этих уравнений. Если ∆H°не зависит от температуры (это справедливо для узкого интервала температур), то из выражения (2.9) получаем 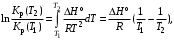 по которому, располагая данными о ∆Н° и Крдлякакой-либо одной температуры Т1 можно легко определить значение константы равновесия при другой температуре Т2. Интегрируя уравнение (2.9) при условии независимости теплового эффекта от температуры, можно вынести ∆Н° из-под знака интеграла и получить следующее уравнение: 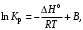 где В – постоянная интегрирования. Так как согласно уравнению изотермы Вант-Гоффа 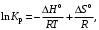 то В = ∆S°/R (при условии независимости ∆Н° и ∆S° от температуры). § 2.4. Расчет равновесия по термодинамическим даннымРасчет константы равновесия и изменения энергии Гиббса позволяет определить равновесный состав реакционной смеси, а также и максимально возможное количество продуктов. Определение констант равновесия химических реакций. В основе расчета констант равновесия для идеальных газов по термодинамическим данным лежат уравнения (2.5) и (2.6). Эти уравнения связывают константу равновесия с изменением энергии Гиббса ∆G°, зависящей от изменения энтальпии ∆Н° и энтропии ∆S°. При этом, поскольку важно не абсолютное значение термодинамических функций отдельных участников реакции, а лишь их изменение, необходимо иметь какую-то точку отсчета. В качестве таковой принято, что для простых веществ (С, О2, Н2 и т. п.) в стандартных условиях и стандартном состоянии (для газов – идеальный газ, для жидкостей – чистая жидкость, для твердого тела – наиболее стабильная при данных условиях модификация) 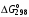 = 0 и = 0 и 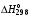 = 0. Тогда каждое сложное соединение можно охарактеризовать стандартной энергией Гиббса = 0. Тогда каждое сложное соединение можно охарактеризовать стандартной энергией Гиббса 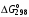 энтальпией энтальпией 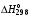 и энтропией и энтропией 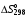 его образования из простых веществ. его образования из простых веществ.Значения термодинамических функций для большого числа простых веществ и соединений приводятся в справочной литературе. Пользуясь справочными данными, можно вычислить стандартные изменения энергии Гиббса, используя правило Гесса. Так, например, для реакции СО2 (г) + 4Н2 (г) 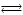 СН4 (г) + 2Н2О (г) СН4 (г) + 2Н2О (г)–394,4 0 –50,8 –228,4 значения 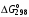 всех участников реакции известны и приведены под уравнением (в кДж/моль). всех участников реакции известны и приведены под уравнением (в кДж/моль).Тогда для реакции 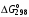 = –50,8 – 2·228,4 + 394,4 = –113,2 кДж/моль. = –50,8 – 2·228,4 + 394,4 = –113,2 кДж/моль.Отсюда легко рассчитать константу равновесия при 298 К: 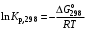 и, следовательно, значение константы равновесия при температуре процесса. Определение констант равновесия сложных реакций осуществляют комбинированием простых реакций. При этом важно выделить и учесть каждую из составляющих простых реакций. Комбинирование необходимо проводить таким образом, чтобы через константы, известные и приводимые в таблицах, можно было выразить константы более сложных реакций или получить по известным константам неизвестные. Так, для последовательных превращений 1) А + B 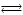 R R2) R 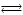 S + Z S + ZA + B 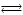 S + Z S + Zконстанта равновесия суммарной реакции равна произведению констант равновесия составляющих ее простых реакций: 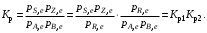 Соответственно, суммарное изменение энергии Гиббса равно сумме ее изменений для отдельных реакций: 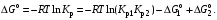 Определение состава реакционной смеси при химическом равновесии. Рассмотрим связь константы равновесия Kр и равновесной степени превращения хa,е для газовой реакции А 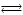 2R. 2R.После установления равновесия на 1 моль введенного вещества реакционная смесь будет содержать (1 – хa,е) моль реагента А и 2хa,е моль продукта R. Всего в равновесном состоянии будет находиться 1 – хa,е + 2хa,е = = 1 + хa,е моль. Если общее давление системы в момент равновесия равно р,можем записать равновесные парциальные давления компонентов согласно выражению (2.8): 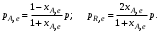 Тогда связь между константой равновесия и равновесной степенью превращения выразится уравнением 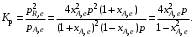 Получили простое уравнение, из которого видно также влияние давления: при постоянной температуре снижение общего давления ведет к увеличению хa,е. Перегруппировав это выражение, получаем 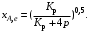 (2.10) (2.10)Расчетная формула (2.10) позволяет найти значения хa,е для разных давлений при постоянной температуре и, следовательно, рассчитать равновесный состав смеси. На рис. 2.1 приведена зависимость равновесной степени превращения реагента хa,е при протекании реакции А 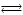 2R от относительного давления 2R от относительного давления 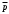 = р/р0, где р0 – стандартное давление, равное 0,098 МПа. = р/р0, где р0 – стандартное давление, равное 0,098 МПа.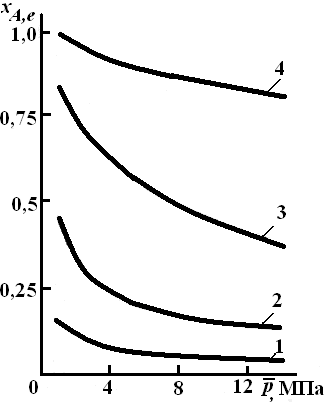 Рис. 2.1. Зависимость равновесной степени превращения обратимой реакции А  2R от давления для разных значений 2R от давления для разных значений константы равновесия Кр:1 – 0,1; 2 – 1,0; 3 – 10,0; 4 – 100,0 Пример 2.1. Рассмотрим расчет равновесия по известным значениям Kр для реакции окисления диоксида серы: SO2 + 0,5О2 + zN2 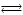 SO3 + zN2, SO3 + zN2,a b n где а, b, n – количество (моль) компонентов исходной смеси SO2, O2, N2, (а + b + n) = 1. Количество каждого компонента (моль) при достижении равновесной степени превращения хA,е составит SO2 O2 N2 SO3 а – ахA,е b – 0,5ахA,е n ахA,е Общее число молей равновесной смеси 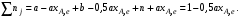 Обозначив общее давление через р, выразим равновесные давления компонентов: 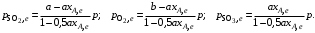 Тогда 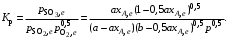 Отсюда 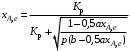 . (2.11) . (2.11)Найдем состав равновесной смеси, если в исходной смеси содержится 7 % SO2, 11 % О2, 82 % N2. При T = 650 К константа равновесия Кр= 629. Подставляя исходные данные в уравнение (2.11), получим 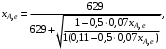 откуда находим хA,е= 0,994 и, следовательно, в равновесной смеси содержится (моль): SO3 – 0,069, SO2 – 0,001, О2 – 0,076, N2 – 0,82. В приведенном примере рассмотрена реакция, протекающая с уменьшением числа молей (∆n < 0). Полученная расчетная формула (2.11) наглядно иллюстрирует зависимость равновесной степени превращения от давления в системе – повышение общего давления ведет за собой увеличение хA,е. |
