ЖБК-№2-SODIQ. Общие данные для проектирования
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
б) на уровне отметке + 18,4 для крайних колонн: – по первой формы колебаний 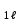 = S = S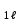 = 43.8 кН; = 43.8 кН; 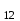 = =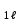 = 43.8 кН; = 43.8 кН;– по второй формы колебаний 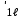 = S = S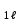 = – 22.9 кН; = – 22.9 кН; 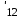 = – 22.9 кН; = – 22.9 кН;–а также для среднего колонна – по первой формы колебаний 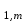 = S = S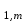 = 86.3 кН; = 86.3 кН; – по второй формы колебаний 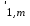 = S = S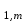 = – 45.1 кН. = – 45.1 кН. в) Расчетные значения перерезывающих сил – на отметке +14,0 м для крайних колонн 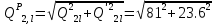 = 84.4 кН; = 84.4 кН;– а также для среднего колонна 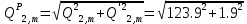 = 123.9кН; = 123.9кН;– а также на отметке + 12,00 для крайних колонн 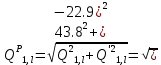 = 49.4 кН; = 49.4 кН;– а также для среднего колонна 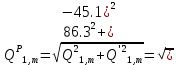 = 97.4 кН. = 97.4 кН.3.5.6.Определение изгибающих моментов от действия сейсмических сил –для крайних колонн на отметке 0,00 м по первой формы колебания М 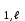 = S = S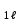 ∙ Н + S ∙ Н + S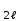 ∙ Н1= 43.8 ∙ 18.4 + 37.2 ∙ 14 = 1326.7 кН∙м; ∙ Н1= 43.8 ∙ 18.4 + 37.2 ∙ 14 = 1326.7 кН∙м;а также по второй формы колебания М 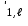 = S = S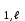 ∙ Н + S ∙ Н + S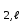 ∙ Н1= - 22.9 ∙ 18,4 + 46.5 ∙ 14 = 229.6 кН∙м. ∙ Н1= - 22.9 ∙ 18,4 + 46.5 ∙ 14 = 229.6 кН∙м.а также на отметке + 14,0 м по первой формы колебания М 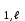 = S = S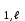 ∙ Н2= 43.8 ∙ 4,4 = 192.7 кН∙м; ∙ Н2= 43.8 ∙ 4,4 = 192.7 кН∙м;по второй формы колебания М 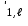 = S = S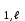 ∙ Н2= - 22.9 ∙ 4.4 = - 100.8 кН∙м. ∙ Н2= - 22.9 ∙ 4.4 = - 100.8 кН∙м.–для среднего колонна на уровне отметки 0,00 м по первой формы колебания: М 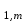 = S = S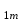 ∙ 18.4 + S ∙ 18.4 + S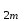 ∙ 14 = 86.3 ∙ 18.4 + 37.6 ∙ 14 = 2114.3 кН∙м; ∙ 14 = 86.3 ∙ 18.4 + 37.6 ∙ 14 = 2114.3 кН∙м;по второй формы колебания: М 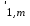 = S = S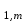 ∙ Н + S ∙ Н + S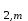 ∙ Н1= - 45.1 ∙ 18.4 + 47 ∙ 14 = -171.8 кН∙м. ∙ Н1= - 45.1 ∙ 18.4 + 47 ∙ 14 = -171.8 кН∙м.а также на отметке + 14,0 м, по первой формы колебания: М 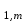 = S = S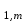 ∙ Н2= 86.3 ∙ 4.4 = 380 кН∙м; ∙ Н2= 86.3 ∙ 4.4 = 380 кН∙м;по второй формы колебания М 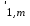 = S = S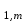 ∙ Н2= - 45.1 ∙ 4.4 = - 198.4 кН∙м. ∙ Н2= - 45.1 ∙ 4.4 = - 198.4 кН∙м.3.5.7.Расчетные значения изгибающих моментов для крайних колонн – на отметке 0,00 м М 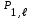 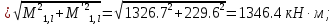 – на отметке 8,50 м М 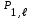 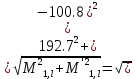 а также для среднего колонна –на отметке 0,00 м М 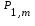 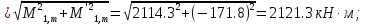 – на отметке 14,0 м М 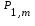 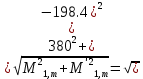 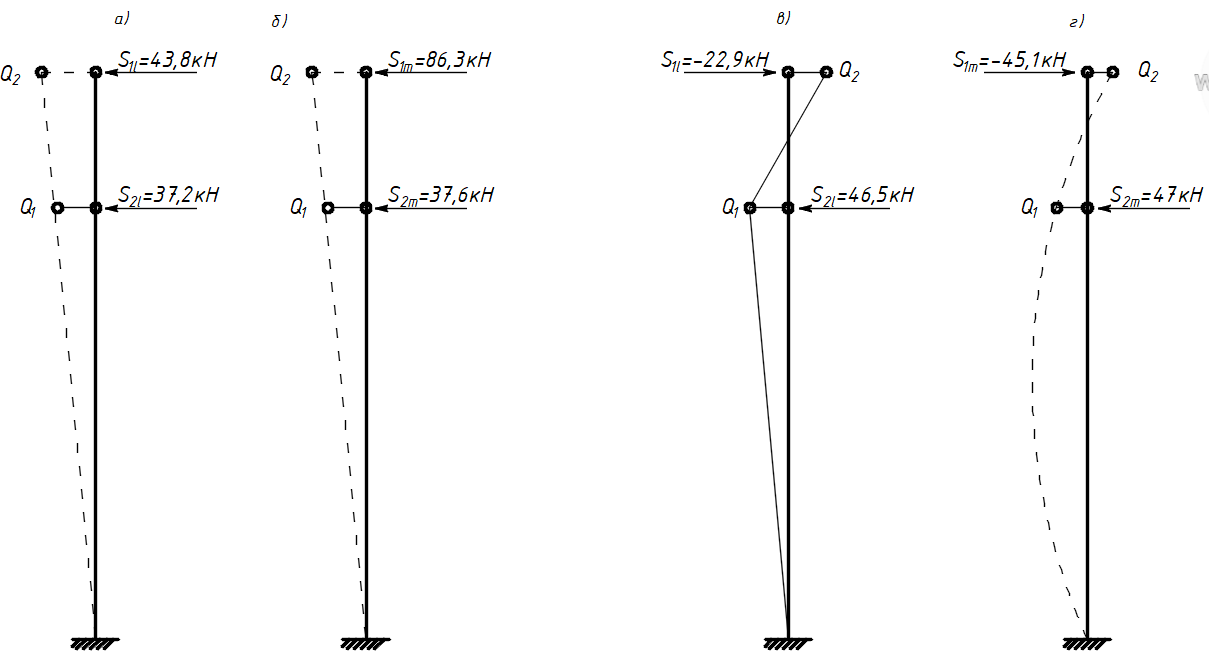 Рис.6. Действие сейсмических сил на отдельные колонны: а) на крайних колонн по 1-й формы колебания, б) на среднюю колонну по 1-й формы колебания, в) а также для крайних и среднего колонна по 2-й формы колебания 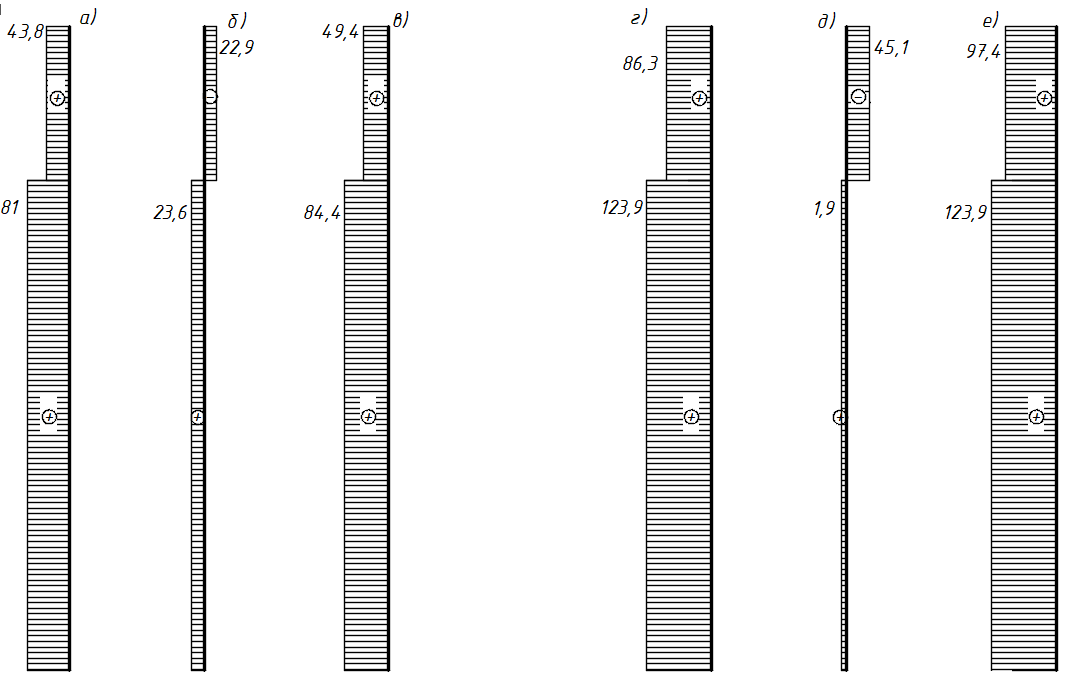 Рис.7. Эпюра поперечных сил от действии сейсмических сил для крайних колонн; а также для средних колонн: а,г) 1-я форма колебания; б,д) 2-я форма колебания; в,е) расчетные значения перерезывающих сил 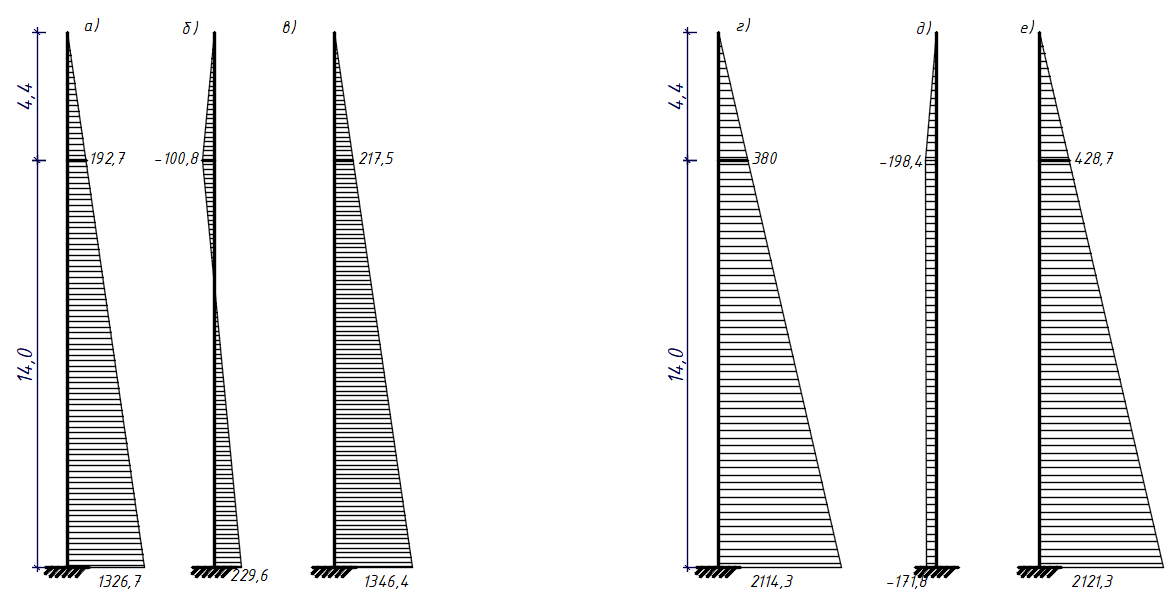 Рис.8. Эпюра изгибающих моментов от действии сейсмических сил для крайних колонн; а также для средних колонн: а,г) 1-я форма колебания; б,д) 2-я форма колебания; в,е) расчетные значения перерезывающих сил 4. Определение усилий в колоннах рамы 4.1. Общие положения. Расчёт рамы выполняют методом перемещений. Неизвестным является ∆1- горизонтальное перемещение верха колонны. Основная система содержит горизонтальную связь, препятствующую этому перемещению. Каноническое уравнение метода перемещений имеет вид: 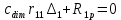 где R1p-реакция верха колонн от внешнего воздействия; cdim –коэффициент учитывающий пространственный характер работы каркаса здания. Постоянная, снеговая, ветровая нагрузки действуют одновременно на все рамы температурного блока, при это пространственный характер работы каркаса не проявляется cdim =1. Крановая же нагрузка приложена только к нескольким рамам блока, однако благодаря жесткому диску покрытия в работу вовлекаются все рамы блока, проявляется пространственная работа, cdim >1. Подвергают основную систему единичному перемещению ∆1=1 и вычисляют реакции верхнего конца сплошной и двухветвевой колонн R∆ по формулам приведённым далее. 4.1.1.Для сплошной крайней колонны: 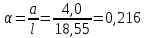 где 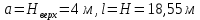 ; ; 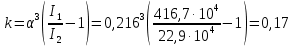 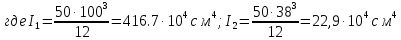 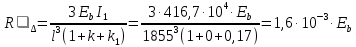 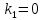 4.1.2.Для средней двухветвевой колонны при числе панелей n=5 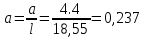 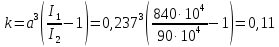 Где 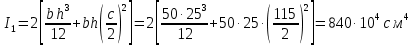 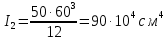 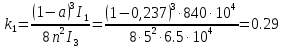 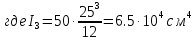 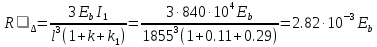 Суммарная реакция 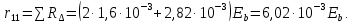 4.2. Усилия в колоннах рамы от постоянной нагрузки Продольная сила F1=201кН на крайней колоне действует с эксцентриситетом e0. В верхней части e0=0, момент M1=F1e0=201∙0=0 В подкрановой части колонны кроме силы F1 приложенной с эксцентриситетом 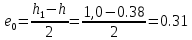 , действуют: , действуют: -расчётная нагрузка от стеновых панелей толщиной 30 см 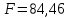 кН с кН с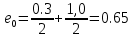 Расчётная нагрузка от подкрановых балок 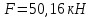 c c 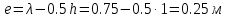 Расчётная нагрузка от надкрановой части колонны F=19.9кН с е0=0.31м Суммарное значение момента 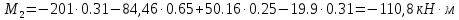 Вычисляют реакцию верхнего конца левой колонны по формуле: 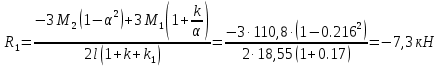 Согласно принятому в расчёте правилу знаков реакция, направленная вправо, положительна. Реакция правой колонны 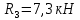 , средней колонны , средней колонны 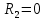 (так как загружена центрально). Суммарная реакция связей в основной системе (так как загружена центрально). Суммарная реакция связей в основной системе 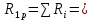 7,3+0-7,3=0, при этом из канонического уравнения 7,3+0-7,3=0, при этом из канонического уравнения 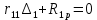 следует, что следует, что 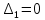 . Упругая реакция левой колонны . Упругая реакция левой колонны 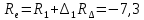 4.2.1. Изгибающие моменты в сечениях колонны (нумерация сечений показана на рис.) равны: 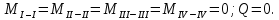 4.2.2. Продольные силы в средней колонне: 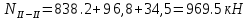 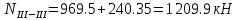 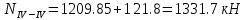 4.3. Усилия в колоннах рамы от снеговой нагрузки Реакция верхней опоры двух крайних колонн. 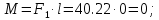 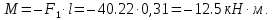 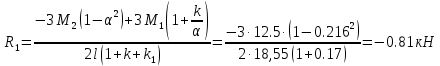 Согласно принятому в расчёте правилу знаков реакция, направленная вправо, положительна. Реакция правой колонны 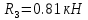 , средней колонны , средней колонны 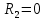 (так как загружена центрально). Суммарная реакция связей в основной системе (так как загружена центрально). Суммарная реакция связей в основной системе 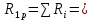 0.81+0-0.81=0, при этом из канонического уравнения 0.81+0-0.81=0, при этом из канонического уравнения 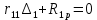 следует, что следует, что 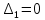 . Упругая реакция левой колонны . Упругая реакция левой колонны 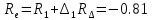 4.3.1. Продольные силы в средней колонне: 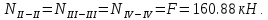 4.4. Усилия в колоннах от крановой нагрузки. Рассматривают следующие виды загружения: 1) 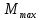 на крайней колонне и на крайней колонне и 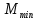 на средней; на средней;2) 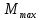 на средней колонне и на средней колонне и 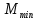 на крайней; на крайней;3) четыре крана с 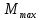 на средней колонне; на средней колонне;4) тормозная сила на крайней колонне; тормозная сила на средней колонне. 4.4.1. Давление D 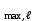 на крайней колонне, на крайней колонне, 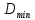 на среднюю колонну на среднюю колоннуВ первом случае на крайней колонне сила 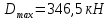 приложена с эксцентриситетом e=0.25м (аналогично эксцентриситету приложения нагрузки от веса подкрановой балки (см. рис.). Момент в узле приложена с эксцентриситетом e=0.25м (аналогично эксцентриситету приложения нагрузки от веса подкрановой балки (см. рис.). Момент в узле 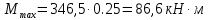 . Реакция опоры левой колонны . Реакция опоры левой колонны 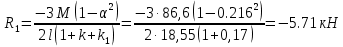 Одновременно на средней колонне действует сила 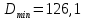 кН эксцентриситетом кН эксцентриситетом 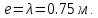 При этом При этом 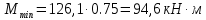 . Реакция опоры средней колонны: . Реакция опоры средней колонны: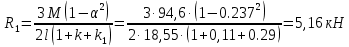 Суммарная реакция в основной системе 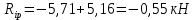 с учётом пространственной работы 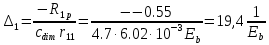 Где 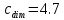 при шаге рам 6м и длине температурного блока 72м. при шаге рам 6м и длине температурного блока 72м.4.4.2.Упругая реакция средней колонны: 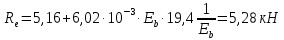 4.4.3. Изгибающие моменты в расчётных сечениях средней колонны: 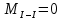 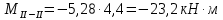 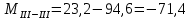 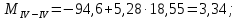 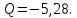 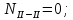 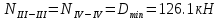 4.4.4. Крановая Н на левой колонне. Реакция верхней опоры двух левых колонн 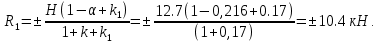 Реакции 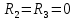 мешавад; ҳосили ҷамъи реаксияҳои мешавад; ҳосили ҷамъи реаксияҳои R 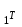 = ± R1=10.4 кН. = ± R1=10.4 кН.Перемещение 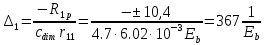 4.4.5. Упругая реакция средней колонны: 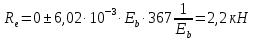 4.4.6. Изгибающие моменты в расчётных сечениях средней колонны: 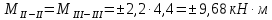 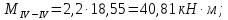 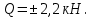 4.4.7. Давление D 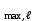 на средней колонне на средней колоннеD 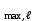 =426,6 кН; D =426,6 кН; D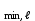 = 84,32 кН приложена в двух крайних колоннах = 84,32 кН приложена в двух крайних колоннахИзгибающий момент на средней колонны от действии вертикальной давление М 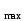 = М = М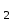 = D = D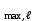 ∙ е ∙ е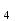 = – 426,6 ∙ 0,75 = – 320 кН∙м. = – 426,6 ∙ 0,75 = – 320 кН∙м. Одновременно на средней колонне действует сила 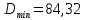 кН эксцентриситетом кН эксцентриситетом 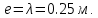 М М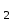 = М = М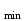 = D = D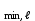 ∙ е ∙ е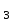 = 84,32 ∙ = 84,32 ∙ 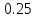 =21,1 кН∙м. =21,1 кН∙м.Реакция опоры левой колонны 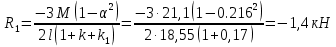 Реакция опоры средней колонны: 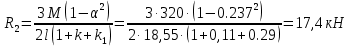 Суммарная реакция в основной системе 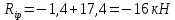 с учётом пространственной работы 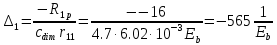 Где 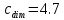 при шаге рам 6м и длине температурного блока 72м. при шаге рам 6м и длине температурного блока 72м. |
