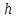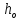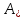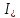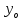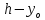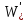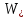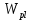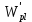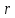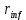ЖБК-№2-SODIQ. Общие данные для проектирования
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
8. Расчет балки по предельным состояниям второй группы 8.1. Геометрические характеристики сечений Отношение модулей упругости арматуры и бетона для стали класса 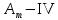 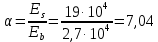 Приведенная площадь сечения К-К (рис. 1 г.) без учета ненапрягаемой арматуры, при 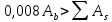 , без учета продольной арматуры. , без учета продольной арматуры.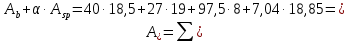 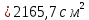 Статический момент приведённого сечения относительно нижней грани балки 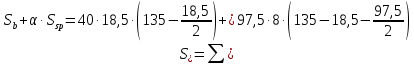 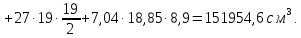 Расстояние от нижней грани сечения до центра тяжести приведенного сечения 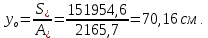 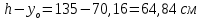 Момент инерции приведенного сечения относительно его центра тяжести 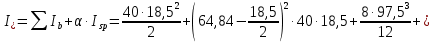 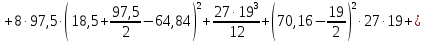 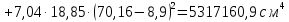 Момент сопротивления приведенного сечения для нижней грани 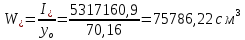 Для верхней грани 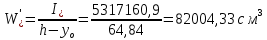 Упругопластический момент сопротивления по растянутой зоне, согласно формуле 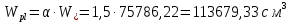 при 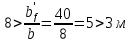 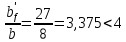 Коэффициент 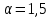 Упругопластический момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента 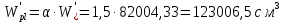 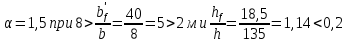 Расстояние от ядровой точки, наиболее удалённой от растянутой зоны (верхней), до центра тяжести приведенного сечения согласно формуле 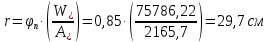 Здесь 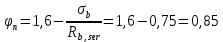 То же, наименее удаленной от растянутой зоны (нижней) 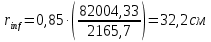 Отношение напряжения в бетоне от нормальных нагрузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы предварительно принимаем равным 0,75. Расстояние от центра тяжести приведенного сечения до равнодействующей усилий в напрягаемой арматуре 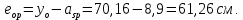 Аналогично вычисляем геометрические характеристики сечения И-И. Результаты расчетов сводим в таблицу. Табл.9.
8.2. Определение величины потер предварительного напряжения арматуры Значения предварительного напряжения назначать таким образом, чтобы для стержневой и проволочной арматуры выполнялись условия 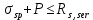 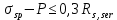 Значение «P» при электротермическом способе вычисляется по формуле 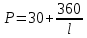 где, P – в МПа; l – длина натягиваемого стержня (расстояние между наружными гранями упоров), м. 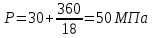 Проверяем условие: 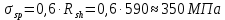 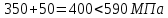 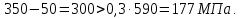 Сечение К – К Первые потери (до окончания обжатия) 1. От релаксации напряжений в арматуре при электротермическом способе натяжения. 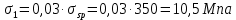 2.От температурного перепада между натянутой арматурой и упорами 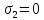 , т.к. пропаривании форма с упорами нагревается вместе с изделиями. , т.к. пропаривании форма с упорами нагревается вместе с изделиями.Усилие обжатия 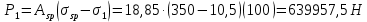 Эксцентриситет этого усилия относительно центра тяжести приведенного сечения 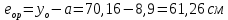 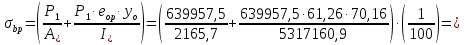 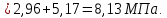 Устанавливаем величину передаточной прочности бетона из условия 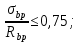 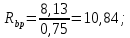 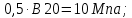 принимаем принимаем 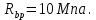 Тогда отношение Тогда отношение 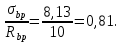 Вычисляем сжимающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия 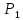 и с учетом изгибающего момента от веса балки. и с учетом изгибающего момента от веса балки.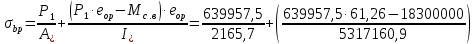 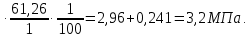 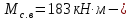 момент от собственного веса балки, согласно табл.3 момент от собственного веса балки, согласно табл.33.Потери от быстронатекающей ползучести при 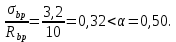 Где 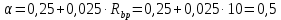 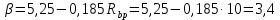 Принимаем 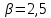 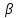 принимается не более 2,5 и не менее 1,1. принимается не более 2,5 и не менее 1,1.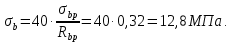 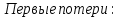 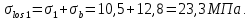 Усилие обжатия с учетом потери 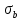 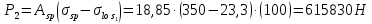 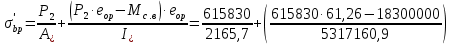 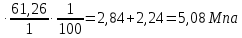 Вторые потери (после обжатия бетона) 4. От усадки бетона 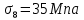 5. От ползучести бетона при 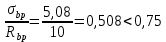 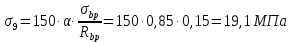 Вторые потери 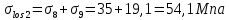 Полные потери 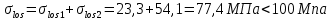 , что меньше установленного минимального значения потерь, принимаем , что меньше установленного минимального значения потерь, принимаем 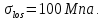 Усилия обжатия с учетом полных потерь 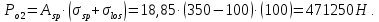 Сечение И-И Аналогично вычислены величины потерь предварительного напряжения и усилия обжатия в сечении И-И (зоне передачи напряжений). При определении 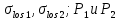 следует учитывать коэффициент условий работы арматуры следует учитывать коэффициент условий работы арматуры 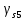 . .В сечении И-И 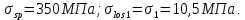 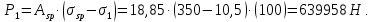 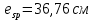 В данном случае 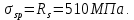 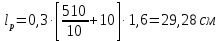 Тогда, 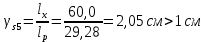 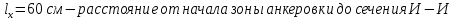 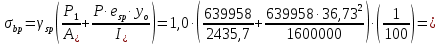 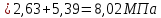 Т.к. 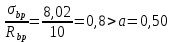 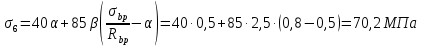 Вычисляем 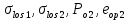 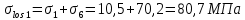 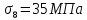 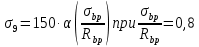 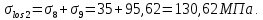 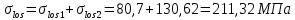 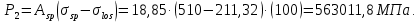 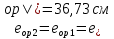 8.3. Расчет по образованию трещин, нормальных к продольной оси балки Данный расчет производится для вынесения необходимости проверки по раскрытию трещин. При этом для элементов, к трещинастойкости которых предъявляется требования 3-й категории, принимаются значения коэффициента надежности по нагрузке 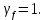 Согласно формуле 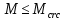 (УП.3) (УП.3) 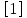 Определяем момент образования трещин по приближённому способу ядровых моментов по формуле (УП.29) 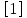 Расчет выполняем для сечения К – К, как наиболее опасного, согласно табл.3 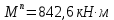 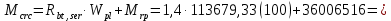 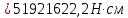 Согласно формуле (УП.30)  или 129 или 129  момент с учетом момент с учетом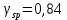 равен: равен: 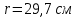 Момент усилия обжатия равен 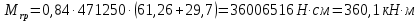 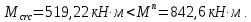 Следовательно, балка в период эксплуатации работает с трещинами в растянутой зоне, приводим расчет по раскрытию трещин. Проверим, образуются ли начальные трещины в верхней зоне балки при её обжатии при значении коэффициента точности натяжения. 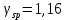 Проверяем условие 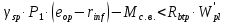 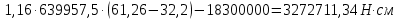 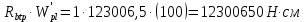 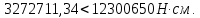 Условие соблюдается, начальные трещины не образуются; Здесь 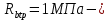 сопротивление бетона растяжению, соответствующее передаточной прочности бетона сопротивление бетона растяжению, соответствующее передаточной прочности бетона 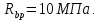 8.4. Расчет по образованию наклонных трещин Расчет проводим для наиболее опасных сечений по длине балки – у на расстоянии 0,6 м от торца (сечении И-И). см. рис 1.д. Проверяем возможность образования наклонных трещин в сечении при действии нормативных нагрузок из условия 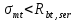 Вычисляем главные растягивающие напряжения по формуле 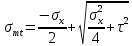 Нормальное напряжение в бетоне на уровне центра тяжести приведенного сечения. 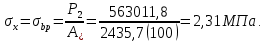 Скалывающее напряжение на уровне центра тяжести приведенного сечения. 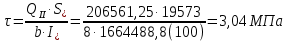 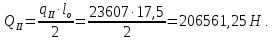 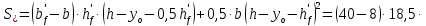 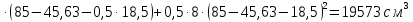 Главные растягивающие напряжения 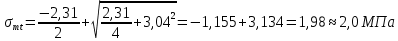 Т.к. условие 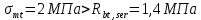 не соблюдается, поэтому необходимо расчет на раскрытию трещин. не соблюдается, поэтому необходимо расчет на раскрытию трещин.8.5. Расчет по раскрытию нормальных трещин к продольной оси балки Расчет ведем для сечение К – К. Предельная ширина раскрытия трещин: непродолжительная 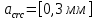 продолжительная продолжительная 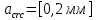 . .Ширину раскрытия трещин определяем по формуле 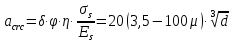 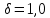 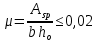 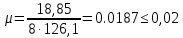 Определение ширины раскрытия нормальных трещин  при непродолжительном действии полной нагрузки. при непродолжительном действии полной нагрузки.Подставляя значение в формуле (15),(13), и (12) находим 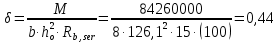 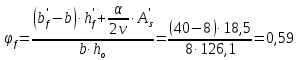 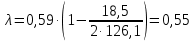 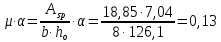 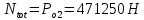 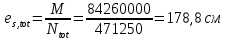 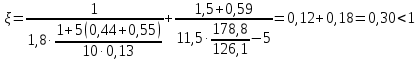 Т.к. 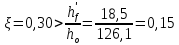 то нейтральная ось проходит по стенке, расчет выполняем как таврового сечения: то нейтральная ось проходит по стенке, расчет выполняем как таврового сечения: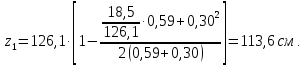 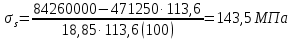 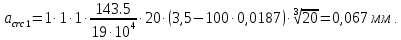 Определение ширины раскрытия нормальных трещин  при непродолжительном действии постоянных и длительных нагрузок. при непродолжительном действии постоянных и длительных нагрузок.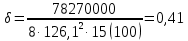 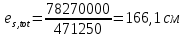 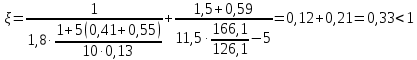 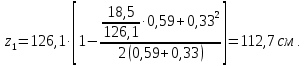 Вычисляем приращение напряжения в арматуре 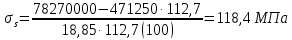 Вычисляем 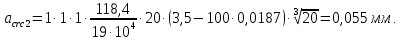 Определение ширины раскрытия трещин 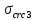 при продолжительном действии постоянных и длительных нагрузок. при продолжительном действии постоянных и длительных нагрузок.Значении 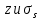 изменяют несущественно и практически могут быть приняты таким же, как при вычислении изменяют несущественно и практически могут быть приняты таким же, как при вычислении 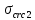 . .Величина 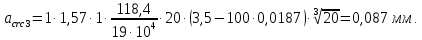 Непродолжительная ширина раскрытия трещин 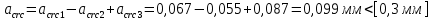 Продолжительная ширина раскрытия трещин 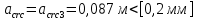 8.6. Расчет по раскрытию трещин к продольной оси балки Ширина раскрытия трещин, наклонных к продольной оси элемента согласно п.4.17 [2] определяется по формуле. 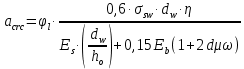 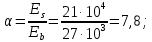 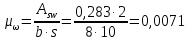 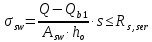 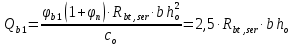 Где 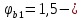 для тяжелого бетона для тяжелого бетона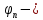 коэффициент, учитывающий влияние продольных сил. коэффициент, учитывающий влияние продольных сил.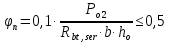 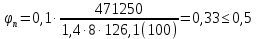 Принимаем 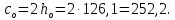 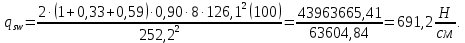 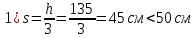 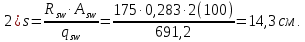 Принимаем 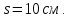 Где 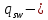 усилие в хомутах на единицу длины балки. усилие в хомутах на единицу длины балки.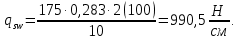 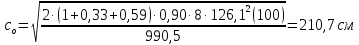 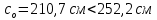 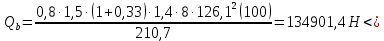 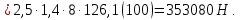 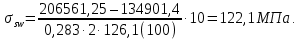 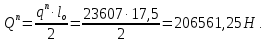 Поперечная сила от действующей постоянной и кратковременной нагрузки. 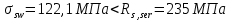 Определение ширины раскрытия наклонных трещин  при непродолжительном действии полной нагрузки при непродолжительном действии полной нагрузки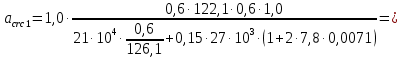 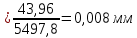 Определение ширины раскрытия наклонных трещин 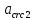 при непродолжительном действии постоянных и длительных нагрузок. при непродолжительном действии постоянных и длительных нагрузок.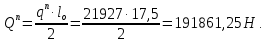 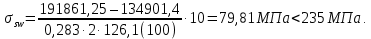 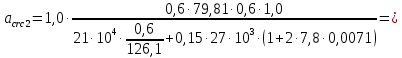 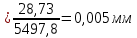 Определение ширины раскрытия наклонных трещин  при продолжительном действии постоянных и длительных нагрузок. при продолжительном действии постоянных и длительных нагрузок.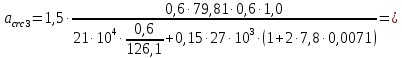 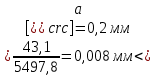 Суммарная величина ширины раскрытия наклонных трещин 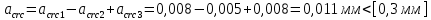 8.7. Расчет прогиба балки Для приближенного расчета прогиба балки используем геометрические характеристики сечения К – К, но при различной длительности действия нагрузки на этом же сечении. Непродолжительное действие всей нагрузки Значение геометрических характеристик берем из расчета раскрытия трещин. 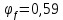 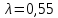 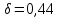 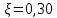 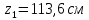 Вычисляем коэффициент, характеризующий неравномерности деформаций растянутой арматуры на участке между трещинами. 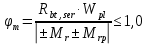 Где 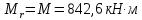 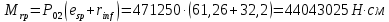 Вычисляем коэффициент, учитывающий работу бетона в растянутой зоне на участке между трещинами. 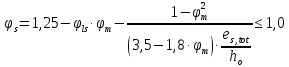 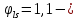 при непродолжительном действии нагрузки при непродолжительном действии нагрузки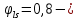 при продолжительном действии нагрузки при продолжительном действии нагрузки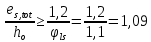 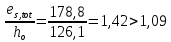 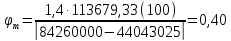 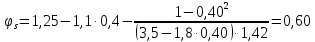 Кривизну определяем по формуле 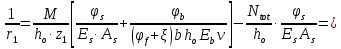 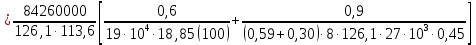 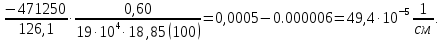 Непродолжительное действие постоянных и длительных нагрузок. Принимаем: 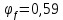 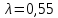 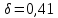 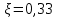 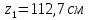 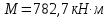 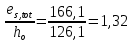 Вычисляем 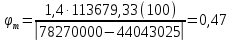 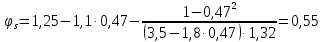 Находим кривизну 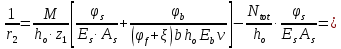 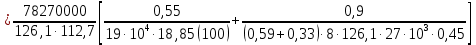 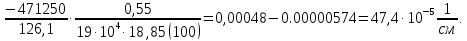 Продолжительное действие постоянных и длительных нагрузок. Принимаем: 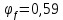 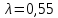 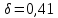 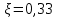 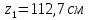 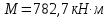 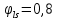 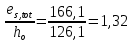 Вычисляем 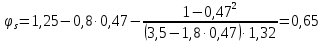 Находим кривизну 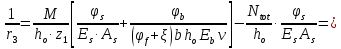 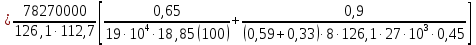 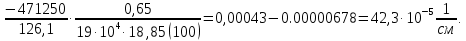 Кривизна 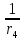 , обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия и определяется по формуле: , обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия и определяется по формуле: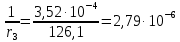 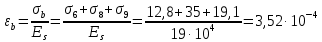 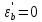 т.к. напрягаемая арматура в сжатой зоне отсутствует. т.к. напрягаемая арматура в сжатой зоне отсутствует.Полный прогиб в середине пролета балки 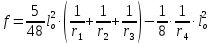 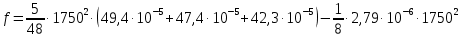 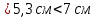 Список использованной литературы 1. СНиП 2.03.01-84. «Бетонные и железобетонные конструкции. Нормы проектирование» М, 1985г. 2. СНиП 2.01.07-85 «Нагрузки и воздействия» М, 1993г. 3. СНиП II-7-81 «Строительства в сейсмических районах» М, 1999г. 4. Байков В.Н., Сигалов Э.Е. - Железобетонные конструкции. Общий курс М,1991 г., 750 стр. 5. Каландарбеков И.И. «Методическое указание по расчету двускатной 18 м балки», Душанбе 1988г., 30стр. 6. Шарипов Л.Ш. - Конструксияҳои оҳанубетонӣ , қисми 3, Душанбе 2013.,634 стр. 7. Корчинский И.Л., Бородин Л.А. и др. «Сейсмостойкое строительство зданий», М,1971г., 281 стр.  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||