ИИТ. Информационно-измерительная техника (иит). Общие сведения Информационноизмерительная техника (иит)
 Скачать 6.71 Mb.
|
Рис. 9. Реализация случайного процессаСлучайные процессы могут быть заданы в непрерывном или в квантованном по времени виде. В последнем случае функция задается выборкой N дискретных значений непрерывной функции, взятых через определенный интервал времени t. При анализе ансамбля реализаций получается наиболее полная информация о случайном процессе. В ряде практически важных случаев можно ограничиться определением характеристик случайного процесса по одной его реализации или по ансамблю значений – это оказывается возможным, если случайный процесс является стационарным. Элементарное измерение характеристик стационарных процессов Полученные в результате измерения эмпирические характеристики случайных процессов принято называть оценками истинных характеристик Q*. Эти оценки сами по себе являются случайными величинами. Поэтому при планировании статистического измерительного эксперимента необходимо решать задачи получения оценок характеристик с заданной погрешностью при ограничениях, накладываемых на объем исходных данных, на время измерения, на возможности аппаратуры и т.п. Оценки характеристик должны быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, отклонения значения которой от оцениваемой величины при увеличении объема статистического материала N стремиться к нулю, т.е.  . Оценка называется несмещенной, если разность ее математического ожидания и истинного значения оцениваемой величины приближается к нулю, т.е. фактически при этом требуется, чтобы отсутствовала систематическая погрешность. Смещение оценки Q* определяется как  . Оценка называется эффективной, если несмещенная оценка обладает наименьшей дисперсией:  . Погрешность оценки Q* обычно определяется доверительной вероятностью Р и доверительным интервалом : .Типовой алгоритм измерения характеристик стационарного случайного процесса по его реализации x(t) может быть представлен в следующем виде:  где H[x(t)] – соответствующее данной оценке преобразование исследуемого процесса. Если x(t) представлено в виде непрерывной функции, что типовой алгоритм реализуется в интегральном виде:  если же исследуемый процесс представлен в виде N дискрет, то  где t – интервал равномерного квантования x(t) по времени. Результат преобразования при измерении математического ожидания H[x(t)] равен  дисперсии  дискрет корреляционной функции  Большинство характеристик, получаемых по описанному алгоритму, состоятельны, несмещенны и эффективны. Исключение составляет оценка дисперсии, и для устранения смещенности она должна быть представлена в виде: 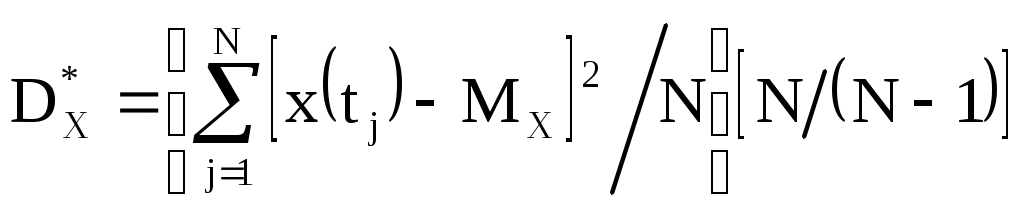 .Основными источниками методической погрешности при реализации этого алгоритма являются конечное время анализа T=Nt или конечный объем выборки N=T/t, квантование x(t) по уровню и способ статистических функций по измеренным их дискретам. Чаще всего при статистическом анализе используются законы распределения вероятностей. 9.2. Системы для измерения законов распределения вероятностей случайных процессов Одномерный интегральный закон, или интегральная функция распределения вероятностей, определяется вероятностями нахождения исследуемого процесса ниже уровня х, который может изменяться от - до +: F(x)=p[- x(t) x] (рис. 10). По определению F(-)=0 и F(+)=1. 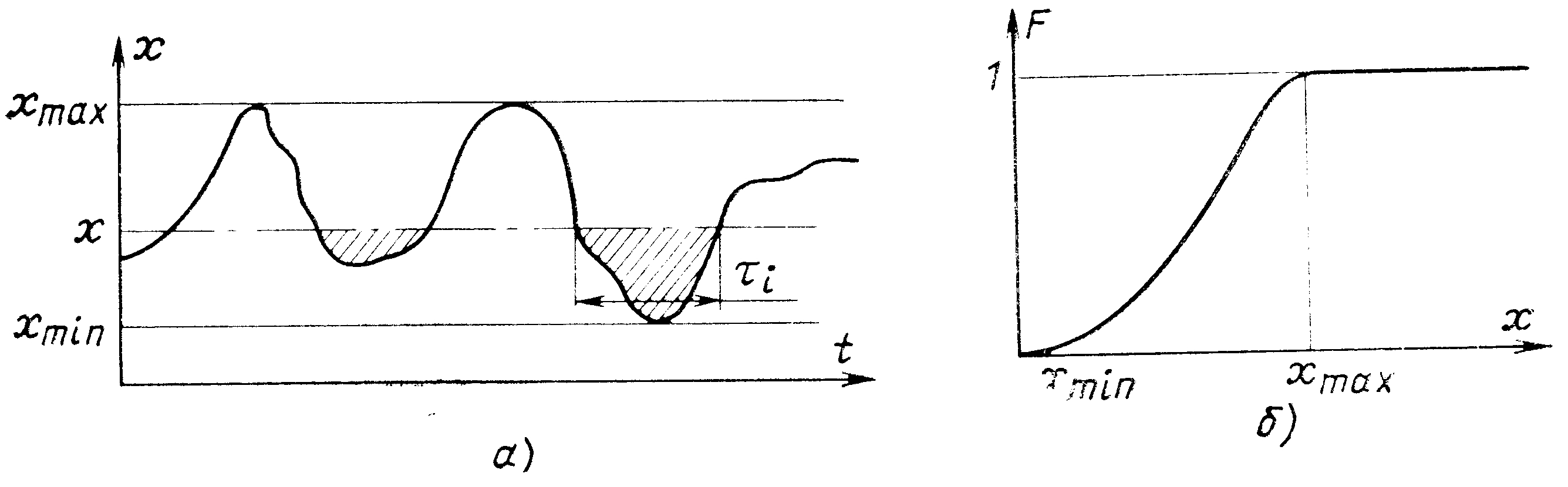 |