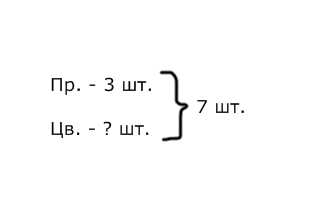Обучение младших школьников решению задач. Обучение младших школьников решению задач. Обучение младших школьников решению текстовых задач
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Виды текстовых задач, изучаемых в начальной школе Все текстовые задачи по числу действий, выполняемых для их решения, делятся на простые и составные. Задача, для решения которой надо выполнить одно арифметическое действие, называется простой. Задача, для решения которой надо выполнить несколько действий, связанных между собой (независимо от того, будут ли это разные или одинаковые действия), называется составной. В свою очередь простые задачи можно разделить на виды либо в зависимости от действий, с помощью которых они решаются (простые задачи, решаемые сложением, вычитанием, умножением, делением), либо в зависимости от тех понятий, которые формируются при их решении Для составных задач нет такого единого основания классификации, которое позволило бы разделить их на определенные группы. Однако в методической литературе из всего многообразия задач выделяются некоторые группы, сходные либо математической структурой (например, задачи, в которых надо сумму разделить на число), либо способом решения (например, задачи, решаемые способом нахождения значения постоянной величины), либо конкретным содержанием (например, задачи на движение) и т.п. Особое внимание уделяется процессу обучения решению задач с пропорциональными величинами: на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестных по двум разностям. Среди которых в рамках отдельной темы рассматриваются задачи, связанные с движением тел. Особенность их изучения связана с равномерным движением объектов. При этом выделяются следующие виды задач на движение: 1. Простые и составные задачи с сюжетами, связанными с движением тел. 2. Собственно задачи на движение (по количеству выполняемых действий): простые, составные. Составные задачи на движение подразделяются: 1) по типу связей между данными и искомым: - на нахождение четвертого пропорционального, - на пропорциональное деление, - на нахождение неизвестных по двум разностям; 2) по особенностям осуществляемого движения: а) для одного объекта: - движение в прямом и обратном направлении, - движение с остановками; б) для двух объектов: - встречное одновременное движение, - одновременное движение в противоположных направлениях, - движение в одном и том же направлении (вдогонку, с отставание). В общем виде систему задач, изучаемых в начальной школе можно представить в виде следующей таблицы (таблица 5): Методика работы с каждым видом задач ведется в соответствии с тремя ступенями: подготовительная, ознакомительная, закрепление. Таблица 5
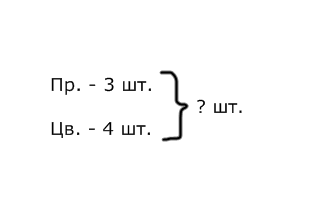
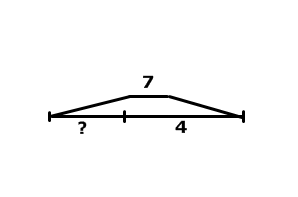
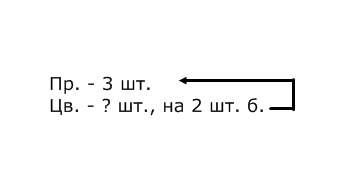
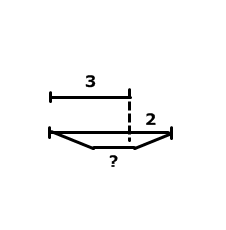
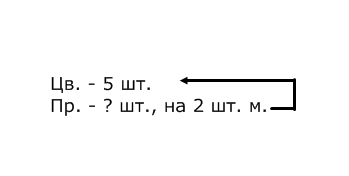
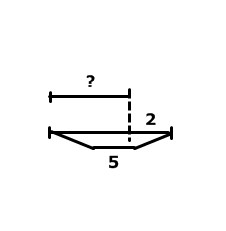
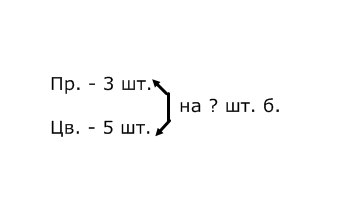
4. Методика обучения младших школьников решению простых задач Простыми называются задачи, решаемые в одно действие. Особенность этих задач – максимальная простота. Они должны быть совершенно понятны, близки детям по сюжету, наиболее просто изложены, не содержать никаких непонятных, новых для детей слов, которые требовали бы дополнительных пояснений. Виды простых задач: Основа классификации – действие, при помощи которого решается задача: на сложение; на вычитание; на умножение; на деление. Основа классификации – смысл арифметического действия: Задачи, направленные на раскрытие смысла арифметических действий. Каждая из этих задач вводится в то время, когда программой предусмотрено ознакомление с соответствующими действиями (сложение, вычитание, умножение, деление). Задачи, раскрывающие различные отношения между числами. В начальном курсе математики особенно много внимания уделяется работе над отношениями между числами, которые могут быть выражены словами «быть равными», «быть на столько-то больше (меньше), чем», «быть во столько-то раз больше (меньше)». Данные задачи могут быть представлены в прямой и косвенной формах: В задачах, выраженных в прямой форме, если содержится выражение «на (во) столько-то меньше», т.е. требуется узнать меньшее число, используется действие вычитание (деление); если содержится выражение «на (во) столько – то больше» – сложение (умножение). В задачах, выраженных в косвенной форме, при встрече с выражением «на (во) столько-то раз больше», используется действие вычитание (деление), если же содержится выражение «на (во) столько – то раз меньше» – сложение (умножение). Задачи, раскрывающие связи между компонентами и результатами арифметических действий. Это задачи на нахождение одного из компонентов действия, когда даны другой компонент и результат. Задачи, связанные с понятиями доли, дроби числа. Задачи, в которых раскрывается зависимость между величинами. Связи между пропорциональными величинами раскрываются с помощью решения простых задач на нахождение одной из величин по данным, соответствующим значениям двух других величин. Дополнительные задачи: задачи – вопросы, задачи – шутки, задачи на смекалку, задачи с недостающими данными или недостающим вопросом, задачи с лишними данными и т.д. Простые задачи на сложение и вычитание Таблица 6
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||