Дипломная работа на тему _ обучение учащихся средней школы решен. Обучение учащихся средней школы решению задач на применение физического смысла производной и первообразной Дипломная работа

• Название: Обучение учащихся средней школы решению задач на применение физического смысла производной и первообразной Дипломная работа
• Дата: 07.05.2023
• Размер: 1.01 Mb.
• Имя файла: Дипломная работа на тему _ обучение учащихся средней школы решен.doc
• Тип: Диплом; #1113691
• страница: 3 из 7

Пример 6. Три резистора сопротивлениями R₁, R₂, R₃ соединены параллельно. Сопротивление R₁ в 9 раз больше сопротивления R₂. Если все три резистора соединить последовательно, то сопротивление цепи равно R.

Определить сопротивления резисторов, при которых сопротивление исходной цепи будет наибольшим.
R ₁ = 9 R₂ Решение:

При параллельном соединении резисторов

R₁, R₂, R₃ сопротивление находится формуле:

1/R_экв = 1/R₁+1/R₂+1/R₃;

R_{экв max}— ? выразим R₃ через R₂:

R₃ = R— R₁—R₂=R—10R₂;

тогда 1/R_экв = (10R—91R₂)/(9R₂(R—10R₂));

Задача сведена к определению наименьшего значения функции в интервале [0;R/10].

Возьмем производную от f(1/R_экв) по R₂ и преобразуем ее:

(1/R_экв)’ = -910(R₂—R/7)(R₂—R/13)/(9R₂² (R-10R₂)²);

В интересующем нас интервале только одна точка R₂ = R/13 в которой эта производная меняет знак с “—” слева на ”+”справа. Поэтому в точке R₂ = R/13 достигается минимум функции 1/R_экв и максимум функции R_экв, при этом

R₁ = 9R/13; R₂ = 1R/13; R₃ = 3R/13;

R_{экв max}= 9R/169;

Пример 7. В магнитном поле с большой высоты падает кольцо, имеющее диаметр d и сопротивление R. Плоскость кольца все время горизонтальна. Найти установившуюся скорость падения кольца, если вертикальная составляющая индукции магнитного поля изменяется с высотой H по закону B = B₀(1 + αH), где α = const.

Решение. Пусть n– нормаль к плоскости кольца, тогда магнитный поток, созданный вертикальной составляющей магнитного поля равна

Ф = BS = B₀(1 + αH)S, где S = πd²/4 – площадь контура.

ЭДС индукции, возникающая в кольце,

E = - Ф’(t) = - (B₀(1 + αH)S)’ = - B₀SαH’(t).

П 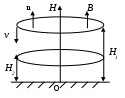роизводная H’(t) = ν_н – это проекция скорости кольца на ось H. Таким образом,

E_i = - B₀Sα( - ν_н).

Так как скорость кольца направлена против оси H, то ν_н = - ν, где ν – модуль скорости кольца и E_i = B₀Sαν.

По кольцу протекает индукционный ток

J = E_i/R = B₀Sαν/R.

В результате в кольце за промежуток времени Δt выделяется количество теплоты

Q = J²RΔt.

На высоте H₁ кольцо обладает механической энергией

W₁ = mgH₁ + mν²/2,

на высоте H₂

W₂ = mgH₂ = mgH₂ + mν²/2

(ν = const, т. е. скорость кольца не меняется). По закону сохранения энергии

W₁ = W₂ + Q => mgH₁ = mgH₂ + J²RΔt => mg(H₁ - H₂) = (B₀Sαν/R)²RΔt =>

mg(H₁ - H₂) = (B₀Sαν)²Δt/R (*)

Разность (H₁ - H₂) есть расстояние, пройденное кольцом при равномерном движении, поэтому H₁ - H₂ = νΔt, и уравнение (*) примет вид:

mgνΔt = (B₀Sαν)²Δt/R => mg = (B₀Sα)²ν/R =>

ν = mgR/(B₀Sα)² = 16mgR/(B₀πd²α)².

Ответ: ν = mgR/(B₀Sα)² = 16mgR/(B₀πd²α)².

Пример 8. Цепь с внешним сопротивлением R = 0,9 Ом питается от батареи из k=36 одинаковых источников, каждый из которых имеет ЭДС E=2 В и внутреннее сопротивление r₀ = 0,4 Ом. Батарея включает n групп, соединенных параллельно, а в каждой из них содержится m последовательно соединенных аккумуляторов. При каких значениях m, n будет получена максимальная J во внешнем R(см. рис.).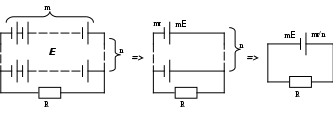



Решение:

При последовательном соединении аккумуляторов E_гр = m*E; r_гр = r₀*m;
а при параллельном соединении одинаковых r_бат = r₀m/n; E_бат = m*E,

По закону Ома J = mE/(R+ r₀m/n) = mEn/(nR + r₀m)

Т.к. k – общее число аккумуляторов, то k = mn;

J = kE/(nR + r₀m) = kE/(nR + kr₀/n);

Для нахождения условия при котором J тока в цепи максимальная исследую функцию J = J(n) на экстремум взяв производную по n и приравняв ее к нулю.

J’_n-(kE(R—kr₀/n²))/ (nR + kr₀/n)² = 0;

n² = kr/R; .

n = √kr/R = √3,6*0,4/0,9 = 4;

m = k/n = 36/4 = 9;

при этом J_max = kE/(nR + mr₀) = 36*2/(4*0,9 + 9*0,4) = 10 А;

Ответ: n = 4, m = 9.

Пример 9. Платформа массой М начинает двигаться вправо под действием постоянной силы F. Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна  кг/с. Пренебрегая трением, найти зависимость от времени ускорения а платформы в процессе погрузки. Определить ускорение а₁ платформы в случае, если песок не насыпается на платформу, а из наполненной высыпается через отверстие в ее дне с постоянной скоростью  кг/с.

Решение.

Рассмотрим сначала случай, когда песок насыпается на платформу

Д 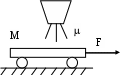вижение системы платформа-песок можно описать с помощью второго закона Ньютона:

dP/dt = F_

P – импульс системы платформа-песок, F_ – сила, действующая на систему платформа-песок.

Если через p обозначить импульс платформы, то можно написать:

dp/dt = F

Найдем изменение импульса платформы за бесконечно малый промежуток времени t:

p = (M+(t+t))(u+u) – (M+t)u =Ft

где u – скорость платформы

Раскрыв скобки и, проведя сокращения получаем:

p = ut + Mu+ut+ ut =Ft

Разделим на t и перейдем к пределу t 0

Mdu/dt+tdu/dt+u=F

или

d[(M+t)u]/dt = F

Это уравнение можно проинтегрировать, считая начальную скорость платформы равной нулю:

(M+t)u = Ft

Следовательно:

u = Ft/(M+t)

Тогда, ускорение платформы:

a = du/dt = (F(M+t)-Ft)/(M+t)² = FM / (M+t)²

Рассмотрим случай, когда песок высыпается из наполненной платформы.

Изменение импульса за малый промежуток времени:

p = (M-(t+t))(u+u) +tu – (M-t)u = Ft

Слагаемое tu есть импульс количества песка, которое высыпалось из платформы за время t

Тогда:

p = Mu - tu - tu = Ft

Разделим на t и перейдем к пределу t 0

(M-t)du/dt = F

или

a₁=du/dt= F/(M-t)

Ответ: a = FM / (M+t)² , a₁= F/(M-t)
Для закрепления данной темы можно предложить следующий набор заданий.

1. Найдите скорость изменения функции в произвольной точке х:

а) у = 6,7х-13

б) g = .

в) f= 3 sin х + ctgx.

2. Найдите скорость изменения функции у = h(х)в точке х₀:

а)

б) h(х) = х³+2х²+1,х₀ =2.

3. Если бы процесс радиоактивного распада протекал равномерно, то
под скоростью распада следовало бы понимать количества вещества, распавшегося в единицу времени. На самом деле процесс неравномерен. Дайте определение скорости радиоактивного распада.

4. 
   Определите понятие силы переменного тока в данный момент времени и дайте выражение для него через производную.
   
5. 
   Тело движется по закону S(t) = 0,5t⁴-5t³+12t²-l. В какие моменты ускорение равно нулю?
   

6. Прямолинейные движения двух материальных точек заданы
уравнениями ( - в метрах, t-в
секундах). Найти ускорения точек в тот момент, когда скорости равны.

7. 
   Угол поворота тела вокруг оси изменяется в зависимости от времени по закону = 0,1t² -0,5t+ 0,2. Найдите скорость вращения тела в момент времени t=20 с.(угол измеряется в радианах).
   
8. 
   Круглый металлический диск расширяется при нагревании так, что его радиус равномерно увеличивается на 0,01 см/с. С какой скоростью увеличивается площадь диска в тот момент, когда его радиус равен 2 см.
   
9. 
   Две точки движутся по одной прямой по законам S = t², S = (t>0).
   

Каковы их скорости в момент встречи? В какой момент времени их скорости одинаковы? Постройте графики движения и поясните на чертеже полученные результаты.

10. Точка массой т₀движется прямолинейно по закону Докажите, что действующая на нее сила пропорциональна квадрату пройденного пути.

11. Материальная точка движется прямолинейно по закону . Найдите мгновенную скорость в момент времени t=24 (S -путь (м), t - время (с)).

12. Материальная точка начинает движение по координатной прямой по закону S = 8 + 30t-5t² (S - путь (м), t - время (с)). При каких значениях t S'(t) =0, S'(t) > 0 ? Какой содержательный смысл имеют эти соотношения?

13. Пусть при прямолинейном движении тела его координата хменяется по закону x(t) = 5t + cos3t-2sin где t- время (с). Найдитеначальную скорость и начальное ускорение тела.

14.Тело движется вертикально по закону h(t) = 2 + 9t-5t². Определить скорость тела в момент его приземления, если h выражается в метрах, t в секундах.

15 .Угол поворота тела вокруг оси изменяется в зависимости от времени t по закону f(t) = 0,1t² -0,5t+ 0,2 . Найдите угловую скорость (рад/с) вращения тела в момент времени t=20c.

16.Составьте аналогичную задачу, в которой какая-нибудь физическая величина выражалась бы при помощи производной.

17. 
    Две точки, движущиеся по одной прямой, подчиняются следующим законам движения: S= t² +2,S= 2t-1 (t > 0). Постройте графики движения. С какой скоростью удаляются эти точки друг от друга в момент, когда одна из них (какая?) догонит другую?
    

18. Две точки движутся по одной прямой по законам S = t²,

S = . Каковы их скорости в момент встречи? В какой момент времени их скорости одинаковы? Постройте графики движения и поясните на чертеже полученные результаты.

19.Докажите, что движение по кубическому закону S = at³ +bt² +ct + dпроисходит с ускорением, меняющимся линейно.

От прямых задач можно перейти к обратным, для чего необходимо поменять местами признаки условия и заключения:

20. Координата точки, движущейся вдоль оси ох изменяется по закону x(t) = -4t² + 2t + 2. Найдите, в какой момент скорость будет равна 1.

21. Точка движется прямолинейно по закону х(t) = + 3sint+ 2t² (t- время (с), х - координата (м)). Найдите:

1. 
   момент времени t, когда ускорение точки равно нулю;
   
2. 
   скорость движения точки в этот момент.
   

22. В какие моменты времени ток в цепи равен нулю, если количество электричества, протекающего через проводник, задается формулой q = 2t- +3.

23 .Предложена следующая задача: «В тонком неоднородном стержне длиной 25 см его масса (г) распределена по закону m= 2l²+3l, где l - длина стержня, отсчитываемая от его начала. Найдите линейную плотность в точке, отстоящей от начала стержня на 3 см». Составьте обратную задачу.

24. По прямой движутся две материальные точки по законам x₁(t) = lnt-3 и x₂(t) = 2t² +6t-1. В каком промежутке времени скорость первой точки больше скорости второй точки?

25.Тело, выпущенное вертикально вверх со скоростью V₀, движется по закону h(t) = V₀t- , где h - путь (м), t - время (с). Найдите наибольшую высоту, которой достигнет тело, если К₀=60 м/с, g=10м/с².

26. Девочка, находясь на балконе, бросает вертикально вверх мяч с начальной скоростью 4 м/с. Мяч движется по закону h(t) = h₀+ V₀t- . Найдите высоту полета мяча в момент времени, когда скорость мяча в 3 раза меньше первоначальной, если расстояние от балкона до земли 3 м, рост девочки 1 м, g = 10м/с² .

При помощи метода соединения, зная следующие положения физики:

сила F = та ; импульс p = mv;

кинетическая энергия Е_к =

и, учитывая ранее изученный материал, можно предложить решить следующие задачи:

27. Тело массой 2 кг движется прямолинейно по закону x(t) = (3t - l)(3t+ 3) - 20
(t - время (с), х - координата (м)). Найдите импульс точки при t=4.

28. 
    Найдите силу, действующую на материальную точку массой m. движущуюся прямолинейно по закону x(t)= при t=2.
    
29. 
    Тело, масса которого m=5 кг, движется прямолинейно по закону
    

S =1-t + t² (S(м),t(c)). Найдите кинетическую энергию тела Е_к = через 10с

после начала движения.

30. Тело с массой т₀движется прямолинейно по закону S = at² + bt + с (а, Ь, с -постоянные). Доказать, что сила, действующая на тело, постоянна.

31. Точка массой т₀движется прямолинейно по закону

S = .Докажите, что действующая на нее сила пропорциональна квадрату пройденного пути.

32. Точка массой т совершает колебательное движение по закону . Докажите, что сила, действующая на точку, пропорциональна координате х.

Зная закон радиоактивного распада (Т - период полураспада) и периоды полураспада радиоактивных изотопов (их можно узнать из любой справочной таблицы физических величин), можно решить задачи вида:

33. Период полураспада тория ( ) равен 7000 лет. Его масса 100 кг. Определить скорость распада через 350 лет.

34.Недалеко от пункта А совершенно случайно было обнаружено место захоронения двухтонной партии ядерных отходов. Необходимо определить отношение скоростей распада соответственно через 150 и 300 лет, если период полураспада Т=150 лет.

Обладая хорошими знаниями по геометрии, можно ученикам предлагать задачи, при решении которых физическая модель переносится на геометрическую, так, например, зная теорему косинусов, теорему Пифагора, можно предложить следующие задачи:

35. Два тела движутся под углом 30° друг к другу; уравнение движения
первого тела S₁(t) = t² -2t, а уравнение движения второго тела S₂(t) = 2t. В
момент времени е=0 тела находились в одной точке. С какой скоростью
увеличивается расстояние между телами?

36. 
    Два тела движутся под углом 60° друг к другу. Первое - равномерно со скоростью 15 км/ч, второе - по закону S(t)=(t-l)(3t+l). С какой скоростью они удаляются друг от друга?
    
37. 
    Бортовые огни малых судов можно различить в море на расстоянии до 1 мили. Корабль А идет на юг, делая 6 миль в час, и в некоторый момент находится в 5 милях от корабля В, который идет на запад со скоростью 7 миль в час. Будут ли корабли друг от друга на расстоянии, достаточном для приема бортовых сигналов? И наоборот, от какой-нибудь, например, геометрической модели можно перейти к физической. Для этого в задаче сначала необходимо определить функцию изменения какой-либо величины:
    

38. Одна сторона прямоугольника имеет постоянную величину а=10 см, а
другая, Ь, изменяется, возрастая с постоянной скоростью 4 см/с. С какой
скоростью растут диагональ прямоугольника и его площадь в тот момент,
когда b=30 см?

39. Радиус круга R изменяется по закону . С какой скоростью
изменяется его площадь в момент времени t=10 с?

40. Ребра прямоугольного параллелепипеда a, b и с изменяются по законам

a = (2t²-1)см, см. c = (4t² +t-3) см. С какой скоростью

изменяются его объем и полная поверхность в момент t=2 сек?

41. На рисунке 3 показана зависимость пройденного пути от времени в начале движения автомобиля. Автомобиль достигает максимальной скорости в момент времени

1.5 с

2.10 с

3.15c

4.из графика определить невозможно



Рис.3

42. На рисунке представлен график зависимости координаты тела от времени при гармонических колебаниях. Какой из графиков на втором рисунке выражает зависимость импульса колеблющегося тела от времени?

1.1

2.2

3.3

4.4



Рис. 4 рис. 5

43. Известно, что тело массой 5 кг движется прямолинейно по закону s(t)= t²+2. Найдите кинетическую энергию тела через 2 с после начала движения.

44. Найдите силу F, действующую на материальную точку с массой 10 кг, движущуюся прямолинейно по закону x(t) = 2t³-1² при t = 2с.

45. Движение материальной точки описывается уравнением

. Определите максимальные значения скорости и ускорения.

46. Колебательное движение точки описывается уравнением

х = 0,05 cos 20 t. Найти координату, скорость и ускорение спустя 1/60 с после момента времени t = 0.

47. 
    Закон изменения температуры тела в зависимости от времени задаётся уравнением Т = 0,2t². С какой скоростью изменяется температура тела в момент времени 5 с?
    
48. 
    Изменение силы тока в зависимости от времени задано уравнением I = 2t² - 5t. Найдите скорость изменения силы тока в момент времени 10 с.
    

49. 
    Маховик вращается вокруг оси по закону = t⁴ - 1. Найдите его угловую скорость w в момент времени t и t=2 с.
    
50. 
    При вращении проволочной рамки в однородном магнитном поле пронизывающий рамку магнитный поток изменяется в зависимости от времени по закону Ф = 10-2cos 10 t Вычислив производную Ф,t , написать формулу зависимости ЭДС от времени . Определить максимальное значение магнитного потока и ЭДС.
    

Тренажеры по теме «физический смысл производной».