Дипломная работа на тему _ обучение учащихся средней школы решен. Обучение учащихся средней школы решению задач на применение физического смысла производной и первообразной Дипломная работа
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Числовой тест. 1. Продолжите числовой ряд: 18 20 24 32 … 2. Продолжите числовой ряд: 212 179 146 113 … 3. Продолжите числовой ряд: 64 48 40 36 34 … 4. Вставьте недостающее число: 2 6 54 18 ? 9 81 27 5. Вставьте пропущенное число: 341 (250) 466 282 ( … ) 398 6. Продолжите числовой ряд: 7 19 37 61 … 7. Вставьте пропущенное число: 8 5 2 4 2 0 9 6 ? Приложение 2. Самостоятельная работа. Восстановите пропущенные цифры в записи умножения 9 5 * * * * 5 * * * * 3 * 2. Найдите сумму целых чисел от 1 до 50 хотя бы двумя способами. 3. Число 64 представлено в виде суммы двух положительных слагаемых так, что сумма их квадратов минимальна. Найдите эти слагаемые. Приложение 3. Приложение 4. Тип урока: обобщающий. Цели: Систематизировать, расширить и углубить знания по данной теме. Способствовать развитию умения сравнивать, обобщать, классифицировать, анализировать, делать выводы. Побуждать учащихся само- и взаимоконтролю, воспитывать познавательную активность, самостоятельность, упорство в достижении цели. Оборудование: экран, кодопозитивы, магнитная доска, папки с приложениями, индивидуальные оценочные листы. Урок происходит по этапам. Результаты каждого этапа учащимся заносят в оценочные листы: Первый этап Повторение Учащиеся в парах повторяют теорию по теме и отвечают друг другу на вопросы (приложения 1, 2 и 3). Правильный ответ оценивается в один балл. М 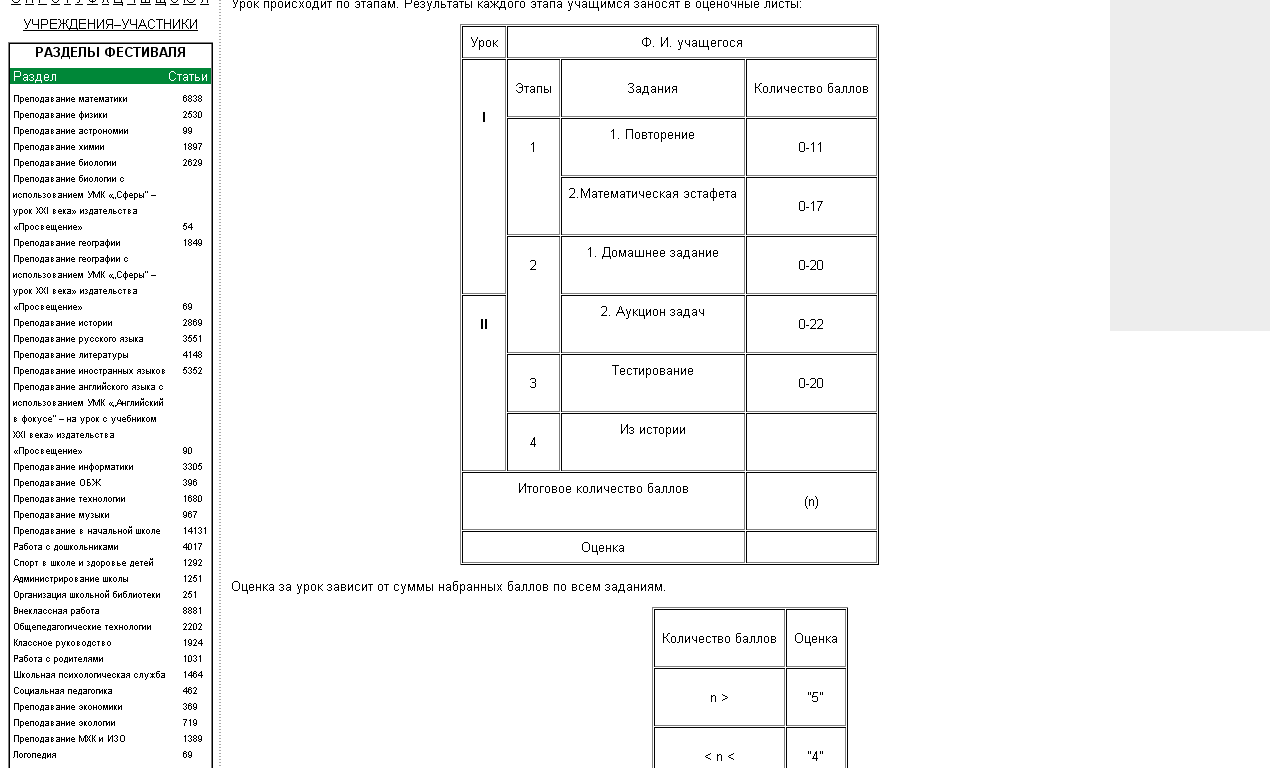 атематическая эстафета атематическая эстафетаРабота в командах. На последней парте каждого ряда находится листок (приложение 4) с 10 заданиями (по 2 вопроса на каждую парту). Первая пара учащихся, выполнив любых два задания, передает листок впереди сидящим. Работа считается оконченной, когда учитель получает листок с правильно выполненными 10 заданиями. Побеждает та команда, которая раньше всех решит все задания. Проверка работ осуществляется с помощью таблицы, помещенной на магнитной доске. (приложение 5). Ученики распределяют между собой заработанное количество баллов, выставляют их в оценочные листы. Второй этап Проверка домашнего задания Учащиеся в парах обмениваются тетрадями и проводят взаимопроверку. 5 ребят заранее заготавливают по одному примеру на карточках для кодоскопа из домашнего задания и комментируют их решение. Предварительное домашнее задание 1) Материальная точка массы m = 1 движется по прямой под действием силы, которая меняется по закону F(t ) = 8 - 12 t. Найдите закон движения точки, если в момент времени t = 0 её координата равна 0 и скорость равна 1. В какой момент времени скорость точки будет максимальной? Решение. F = m a ? (t) = 8 t – 6 t2 + с1, по условию (t) = 0, значит с1 = 1, тогда (t) = 8 t - 6 t2 + 1. x (t) = 4 t2 – 2 t3 + t + c2, так как x (0) = 0, то c2 = 0. Значит x (t) = 4 t2 – 2 t3 + t. Найдем момент времени, когда скорость точки будет максимальной 1(t) = a (t) = 8 – 12 t, 8 – 12 t = 0, t = . Ответ: x (t) = 4 t2 – 2 t3 + t, t = с. 2) Пользуясь геометрическим смыслом определенного интеграла, вычислить . Решение. . Найдем площадь полукруга с центром А (2; 0) и радиусом R=1. Ответ: . 3) При каком а выполняется равенство ? Решение. . По условию задачи , откуда a = - 2 , a = 2. Ответ: -2; 2. 4) Вычислить интеграл . Решение. = = ( - сos5x + cosx) = -. Ответ:. Каждое правильное выполненное задание оценивается классом от 1 до 5 баллов.. Аукцион задач 1) Вычислить площадь фигуры, ограниченной графиком функции у = х и касательными, проведенными к графику в точках х= -1 и х= 2 (5 баллов). 2) В каком отношении парабола у = х делит площадь прямоугольника, вершины которого находятся в точках А (0;0), В (3;0), С (3;9), D (0;9)? (5 баллов). 3) Решите уравнение = 6х - х + у (4 балла). Решите неравенство >= -7х (4 балла). 5) Найдите объем фигуры, полученной вращением криволинейной трапецией, ограниченной линиями у = , у = 1, х = 0, х = 1 (4 балла). Ответы: 1. 2; 2. 1:3; 3. 1; 4. ; 5. . Третий этап Тестирование. Тест №2 [ 2, стр.180 ] Работа проводится по четырем вариантам, в каждом из которых по десять заданий, записанных в таблицу. Решая, ученик записывает варианты ответа на листе ответов. По истечении времени, отведенного на тест, учащиеся обмениваются листами и проводят быструю взаимопроверку. Учитель демонстрирует кодопозитив с ответами к заданиям теста. Каждое правильно решенное задание оценивается двумя баллами. Результаты заносятся в оценочный лист. Четвертый этап Из истории Группа учащихся готовит сообщение о происхождении терминов и обозначений по теме “Первообразная. Интеграл”, из истории интегрального исчисления, о математиках, сделавших открытия по данной теме. Пятый этап Подведение итогов Учитель отмечает, в какой мере достигнуты цели, называет лучших учащихся, лучшую команду, называет оценки, отмечает вопросы, по которым ребятам еще нужно работать, указывает на основные ошибки, планирует индивидуальную работу с теми учащимися, которые допустили ошибки. |
