Дипломная работа на тему _ обучение учащихся средней школы решен. Обучение учащихся средней школы решению задач на применение физического смысла производной и первообразной Дипломная работа

• Название: Обучение учащихся средней школы решению задач на применение физического смысла производной и первообразной Дипломная работа
• Дата: 07.05.2023
• Размер: 1.01 Mb.
• Имя файла: Дипломная работа на тему _ обучение учащихся средней школы решен.doc
• Тип: Диплом; #1113691
• страница: 2 из 7

Глава 2. Организация экспериментальной работы по обучению учащихся средней школы решению задач на применение физического смысла производной и первообразной

При изучении темы «Физический смысл производной и первообразной» необходимо использовать разнообразные задания разных уровней сложности, поскольку даже учащиеся одного класса обладают разной математической подготовкой. В соответствии с этим положением и для осуществления дифференцированного подхода на этапах формирования умений и контроля знаний необходимо использовать разнообразные формы и средства обучения, среди них проведение самостоятельных работ, тестов, решение тренажеров.

§3. 2.1 Описание дидактических материалов для осуществления дифференциации при обучение учащихся средней школы решению задач на применение физического смысла производной и первообразной

Современная математика играет важную роль в естественно научных, инженерно-технических и гуманитарных исследованиях. Она стала для многих отраслей знаний не только орудием количественного расчета, но и методом точного исследования и средством предельно четкой формулировка понятий и проблем. [24,с. 5]

Связи между науками математики, физики, химии и биологии многообразны и постоянны. Школьники изучают производные элементарных функций, интегралы и дифференциальные уравнения. Математика не только дает физики, химии, биологии вычислительный аппарат, но и обогащает их в идейном плане. На уроках математики школьники учатся работать с математическими выражениями [38].Знание понятия производной позволяет количественно оценить скорость изменения физических явлений и процессов во времени и пространстве, например скорость испарения жидкости, радиоактивного распада, изменения силы тока и др. Умение дифференцировать и интегрировать открывает большие возможности для изучения колебаний и волн различной физической природы и вместе с тем для повторения основных понятий механики (скорости, ускорения) более глубоко. (см. рис2).


П

Р

И

Л

О

Ж

Е

Н

И

Е
П

Р

О

И

З

В

О

Д

Н

О

Й



физика

Химия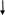








. Скорость движения

материальной точки есть производная от пути по времени

. Скорость протекания химической

реакции (распада вещества) есть производная

от массы вещества, вступившего в реакцию, по

времени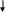







. Ускорение есть

производная скорости по времени или вторая производная пути по времени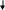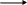







Сила – это производная работы по совершению этой силы по перемещению.

Биология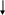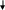





. Сила тока в момент времени t есть производная от количества электричества по времени

Скорость роста популяции бактерий

есть производная от размера популяции по

времени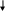






. Мощность есть производная

работы по времени, в течение которого она

совершена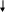







. Теплоемкость при температуре t есть производная от количества электричества тепла, получаемого телом, по температуре.






Линейная плотность стержня в

данной точке есть производная от массы

стержня по его длине.


Рис. 2. Приложения производной

Для того чтобы решать задачи на применение физического смысла производной, предварительно нам необходимо четко сформулировать физический смысл производной.

В школе основное внимание уделяется механическому смыслу производной:

Пусть материальная точка движется по прямой, на которой выбраны начало отсчета, единицы измерения и направление, по закону S = S(t) [S(t)-положение точки на прямой в момент времени t]. Под средней скоростью движения за промежуток времени в физике понимают отношение перемещения к промежутку времени, т.е средняя скорость за промежуток времени от до t₂выражается равенством:



Полагая , получим



Мгновенной скоростью в момент времени t (точнее, численным значением скорости в момент времени t) называют предел средней скорости движения за промежуток времени [ ] при условии . Таким образом,



Поэтому считают, что мгновенная скорость V(t) определена (только) для любой дифференцируемой функции S(t), при этом



Мгновенная скорость может принимать как положительные, так и отрицательные значения и, конечно, значение 0, если скорость на каком-то промежутке времени (t ;t₂) положительна, то точка движется в положительном направлении, т.е. координата растет с течением времени, а если V(t) отрицательна, то координата убывает.

Средняя скорость характеризуется наклоном (точнее, тангенсом угла наклона) хорды к графику движения, а мгновенная скорость - наклоном касательной к этому графику, т.е. производной.

Ускорение произвольного движения определяется как скорость изменения скорости движения, т.е. как производная скорости по времени:

а = V'(t).

Если термин «скорость» понимать в более общем смысле, то, имея функцию y=f(x) можно ставить вопрос в скорости изменения значений переменной у по сравнению со значениями переменной х.

Пусть дана функция y=f(x) и т.х₀, принадлежащая области определения функции f, в которой существует производная f'(x₀). Считают, что f'(x₀) = V(x₀).

Итак, производная данной функции y=f(x) вточке х₀ равна скорости изменения значений функции вточке х₀.

В этом состоит физический смысл производной.

Пример 1.Тело движется по закону . Найдите скорость при t = 9.

Решение.



Воспользуемся физическим смыслом производной.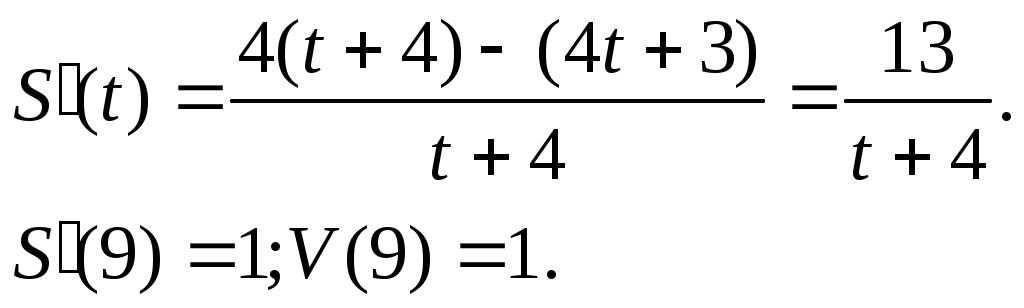



Ответ: 1

Пример 2.

Найдите значение аргумента, при котором скорость изменения значений функции f(x)= 3x²+6xравна 12.

Решение. Для нахождения значения аргумента воспользуемся физическим смыслом производной.



По условию , получаем уравнение 6х₀ + 6 = 12;

х₀ =1.

Ответ: 1

Пример 3. Найдите число значений аргумента из промежутка при которых скорость изменения значений функции f(x)= cos2x равна .

Решение.

V(x) = f'(x).

f'(x) = -2sin2x, m.к. 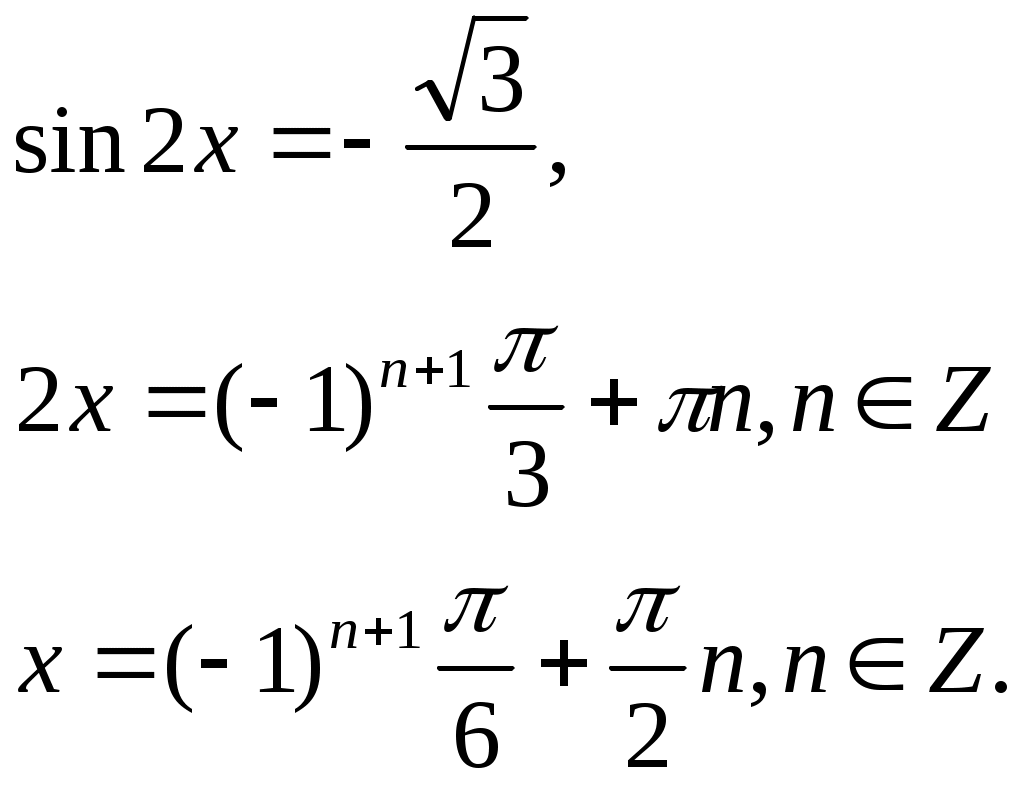, то получим уравнение - 2sin2x = ,



Найдем значения х, входящие в промежуток .

Если n=-2, то

Если n=-1, то

Если n=0, то

Если n=1, то

Если n=2, то

Если n=3, то

Итак, промежутку принадлежат четыре корня уравнения. В найденных точках скорость изменения функции равна .

Пример 4.

Найдите значения аргумента, при которых скорость изменения значений функции f(x) = е^2хбольше скорости изменения значений функции

Решение.

D(f) = (- ;+ ).D( ) = (- ;+ ).

С учетом физического смысла производной, задача сводится к решению

неравенства .



Получаем неравенство решим его.



т.к. то получаем



т.к. е>1, то функция у = log_e tвозрастающая, получаем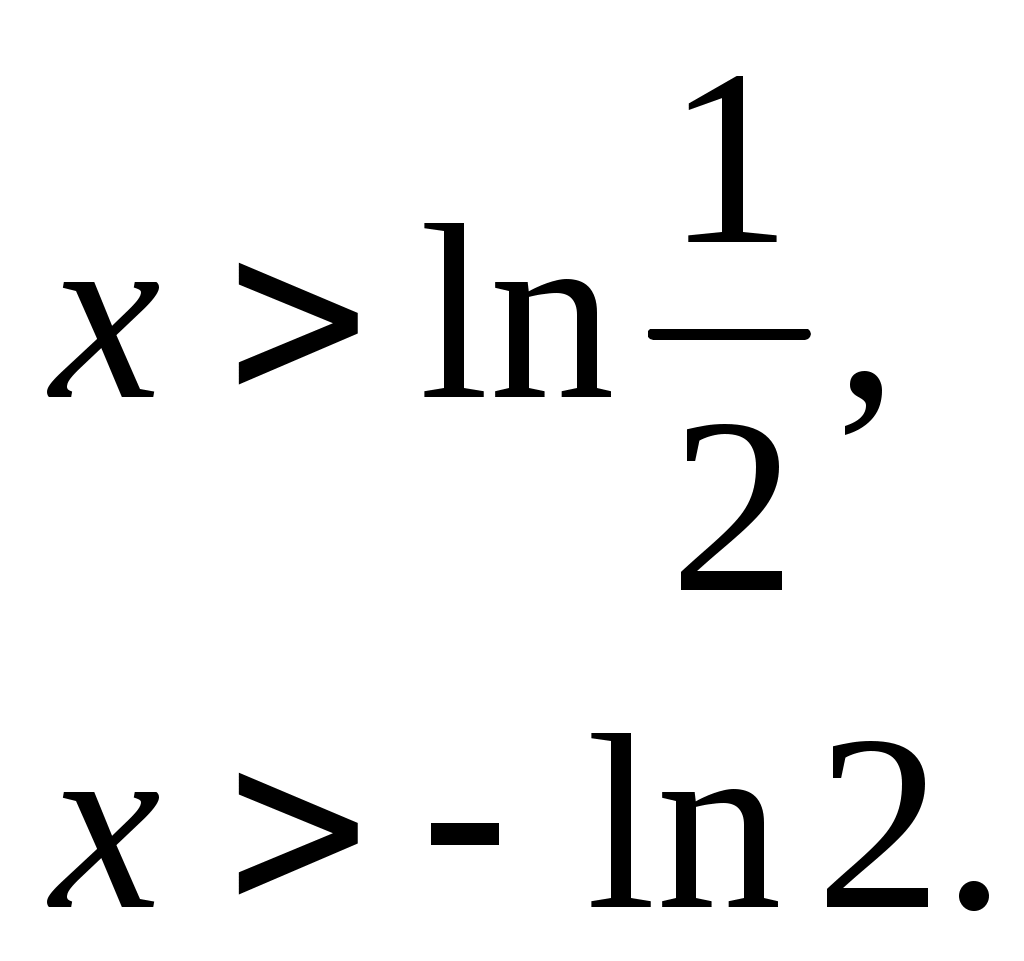



Ответ: .

Пример 5. Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: U = a/r² – b/r, где a и b — положительные постоянные, r — расстояние между частицами.

Найти:

а) значение r₀ соответствующее равновесному положению частицы;

б) выяснить устойчиво ли это положение;

в) F_max значение силы притяжения;

г) изобразить примерные графики зависимости U(r) и F(r).
U = a/r² – b/r; Решение:

a и b — counts; Для определения r₀ соответствующего равновесному

r ₀ — ? положению частицы исследуем f = U(r) на экстремум.

F_max — ? Используя связь между потенциальной энергией поля

U и F, тогда F = -dU/dr, получим F = -dU/dr = - (-2a/r³+b/r²) = 0;

при этом r = r₀; 2a/r³ = b/r² => r₀ = 2a/b;

Устойчивое или неустойчивое равновесие определим по знаку второй производной:

d²U/dr₀²= dF/dr₀=-6a/r₀⁴ + 2b/r₀³ = -6a/(2a/b)⁴+2b/(2a/b)³=(-b⁴/8a³)<0;

равновесие устойчивое.

Для определения F_max притяжения исследую на экстремумы функцию:

F = 2a/r³— b/r²;

dF/dr = -6a/r⁴ + 2b/ r³ = 0;

при r = r₁ = 3a/b;

подставляя, получу F_max = 2a/r³₁ — b/r³₁ = - b³/27a²;

U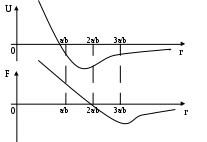
(r) = 0; при r = a/b; U(r)_min при r = 2, a/b = r₀;

F = 0; F(r)_max при r = r₁ = 3a/b;