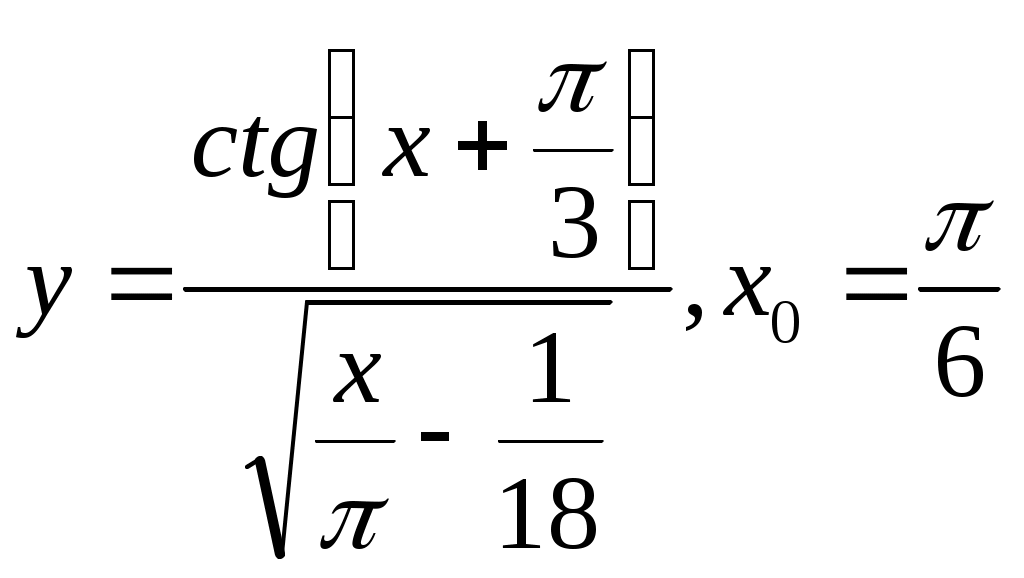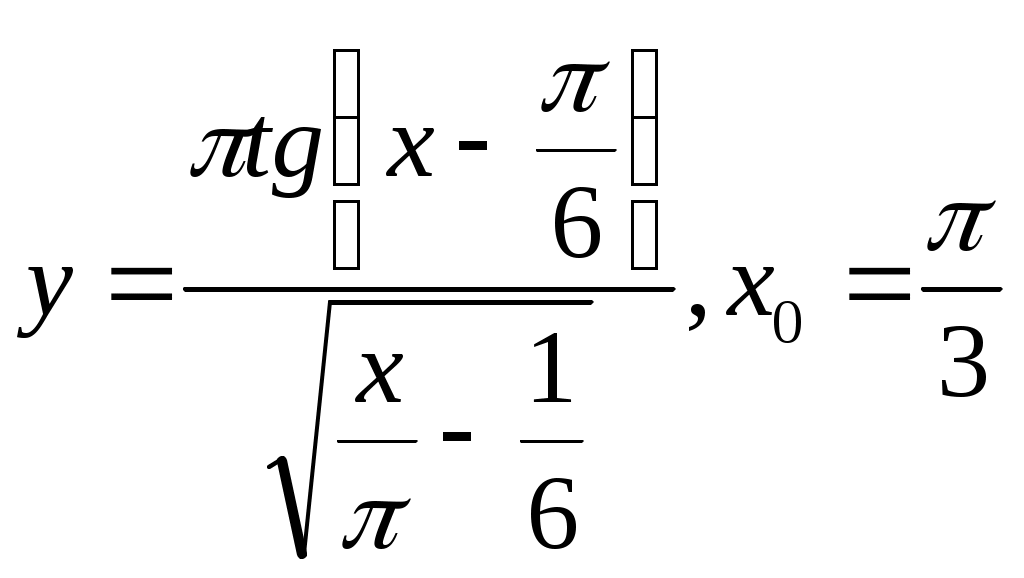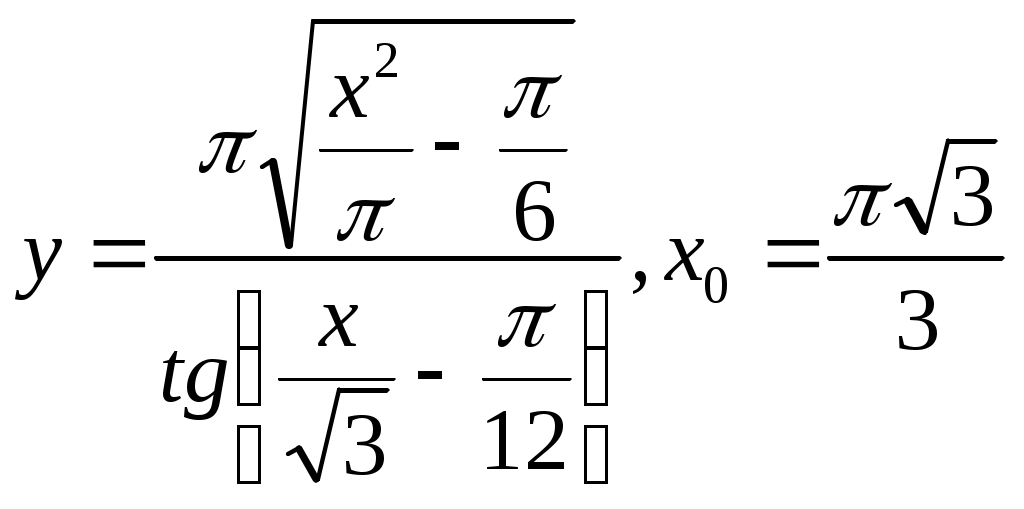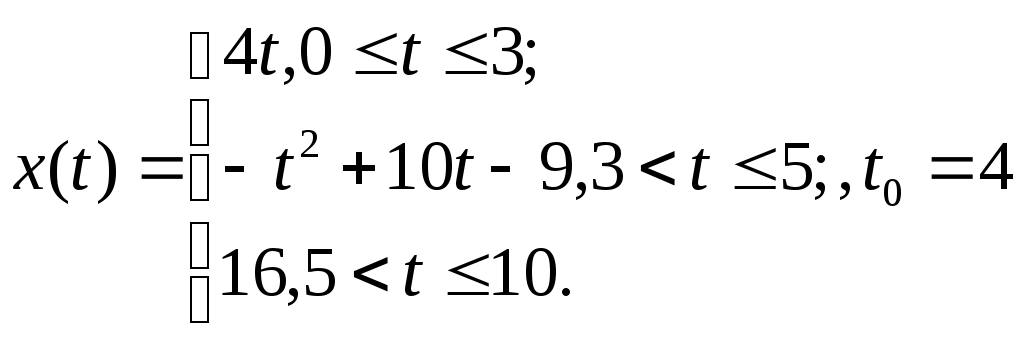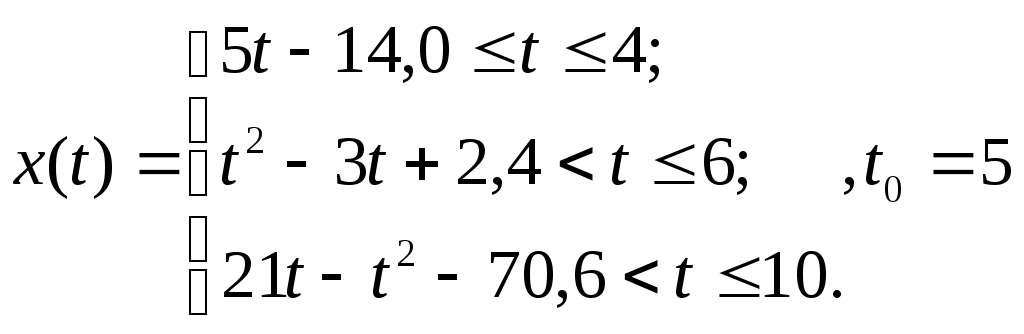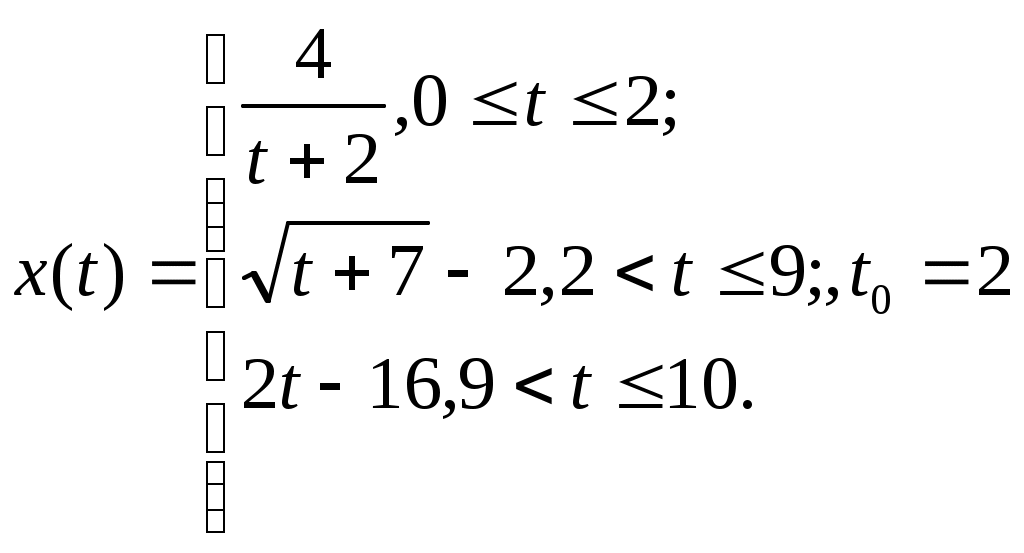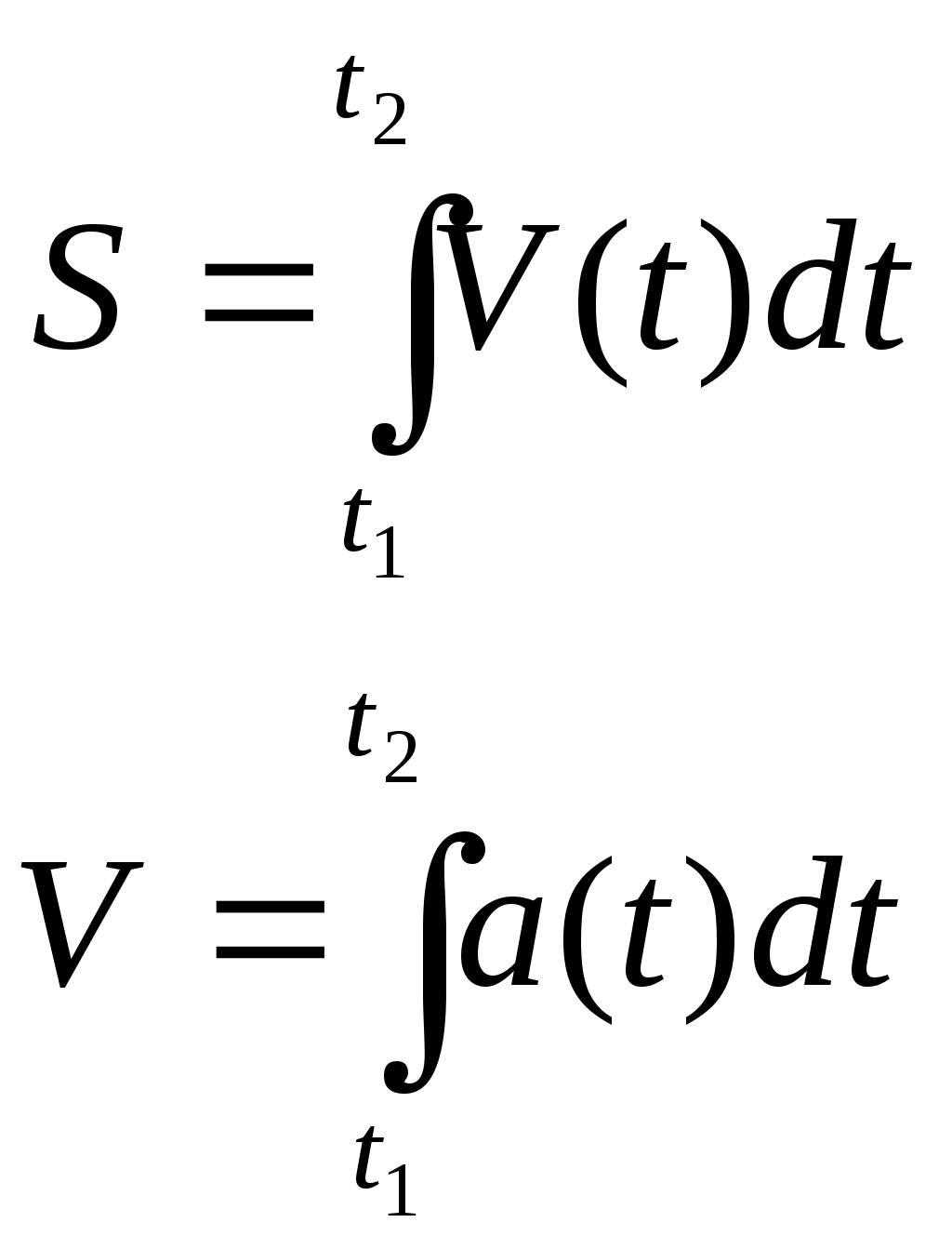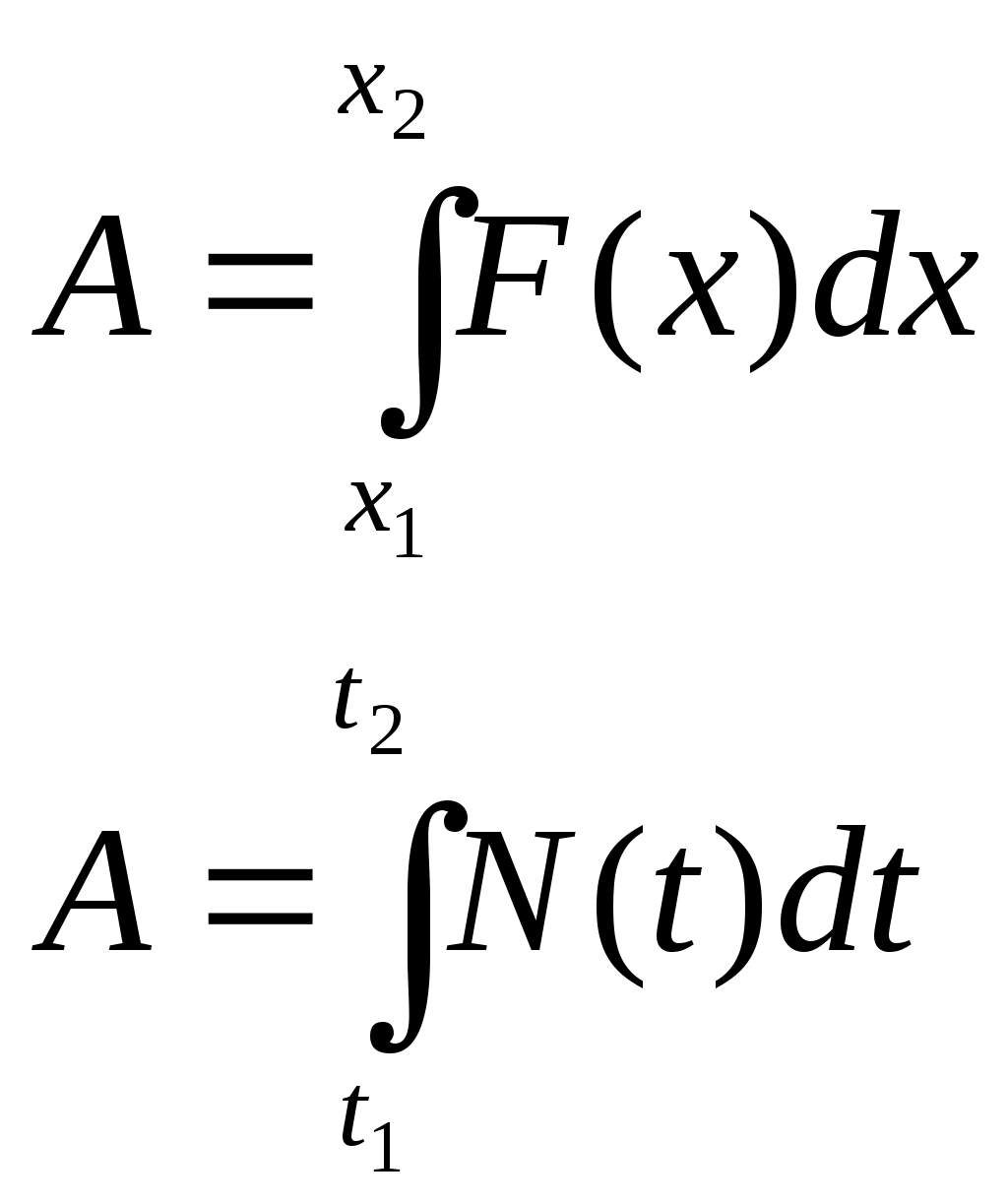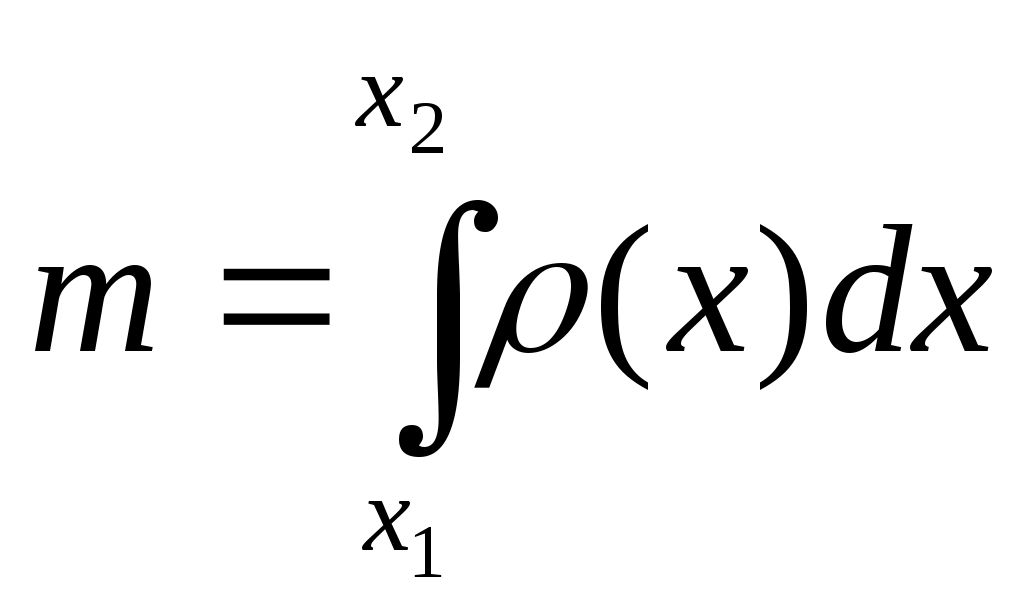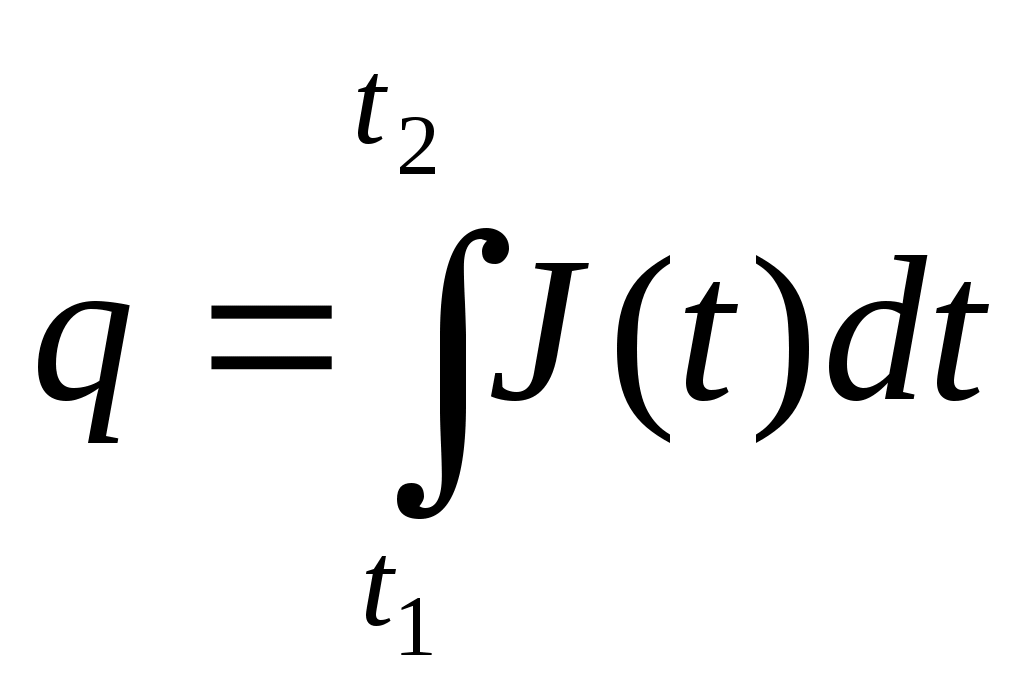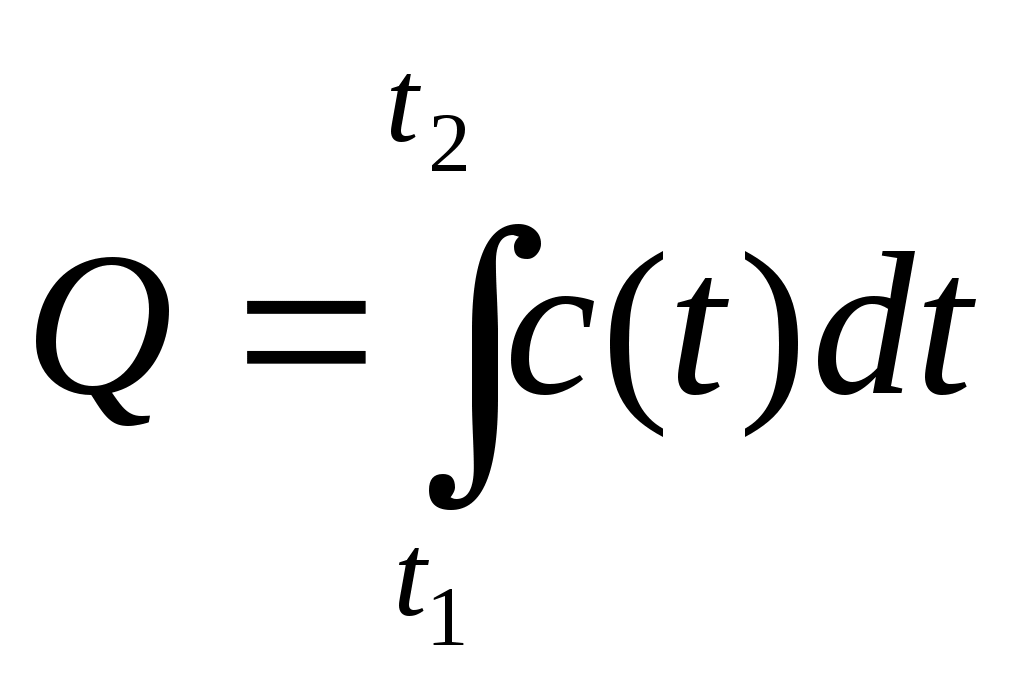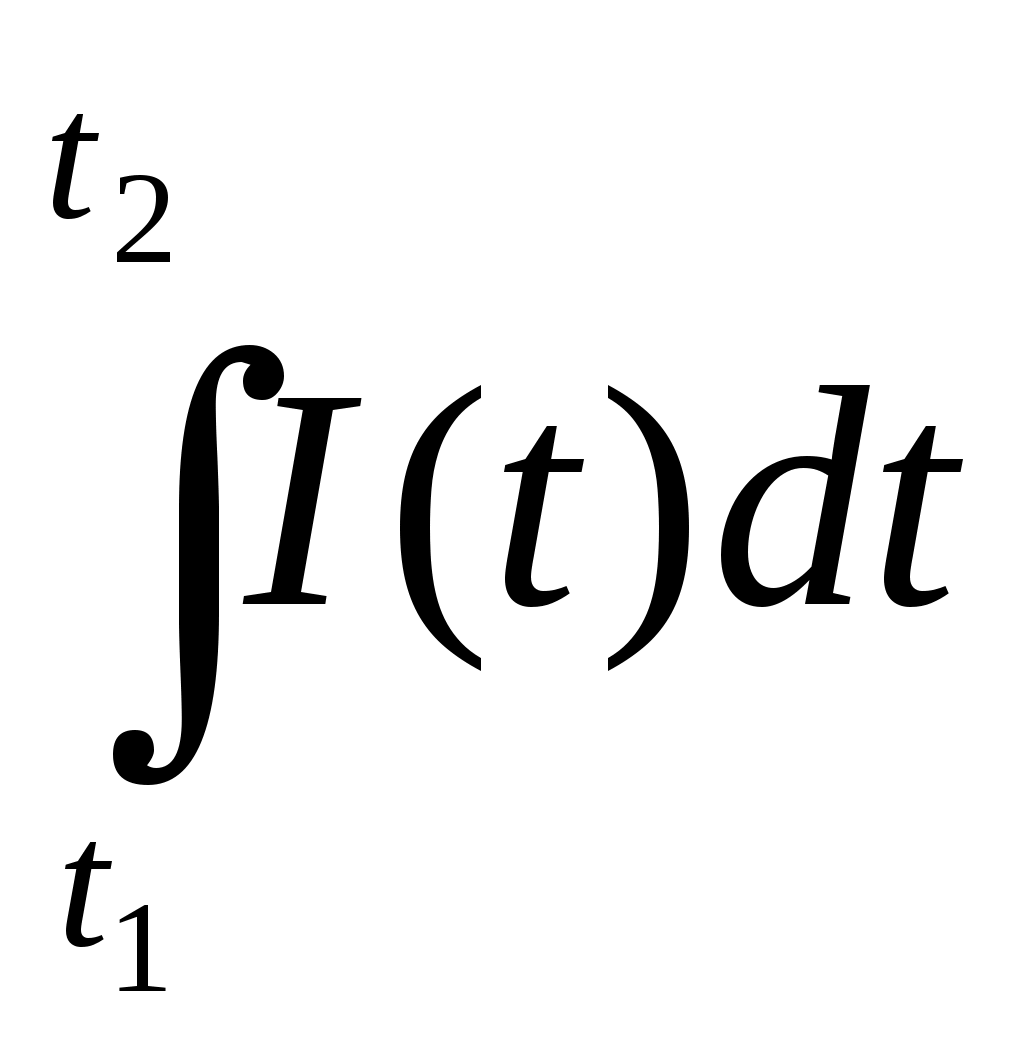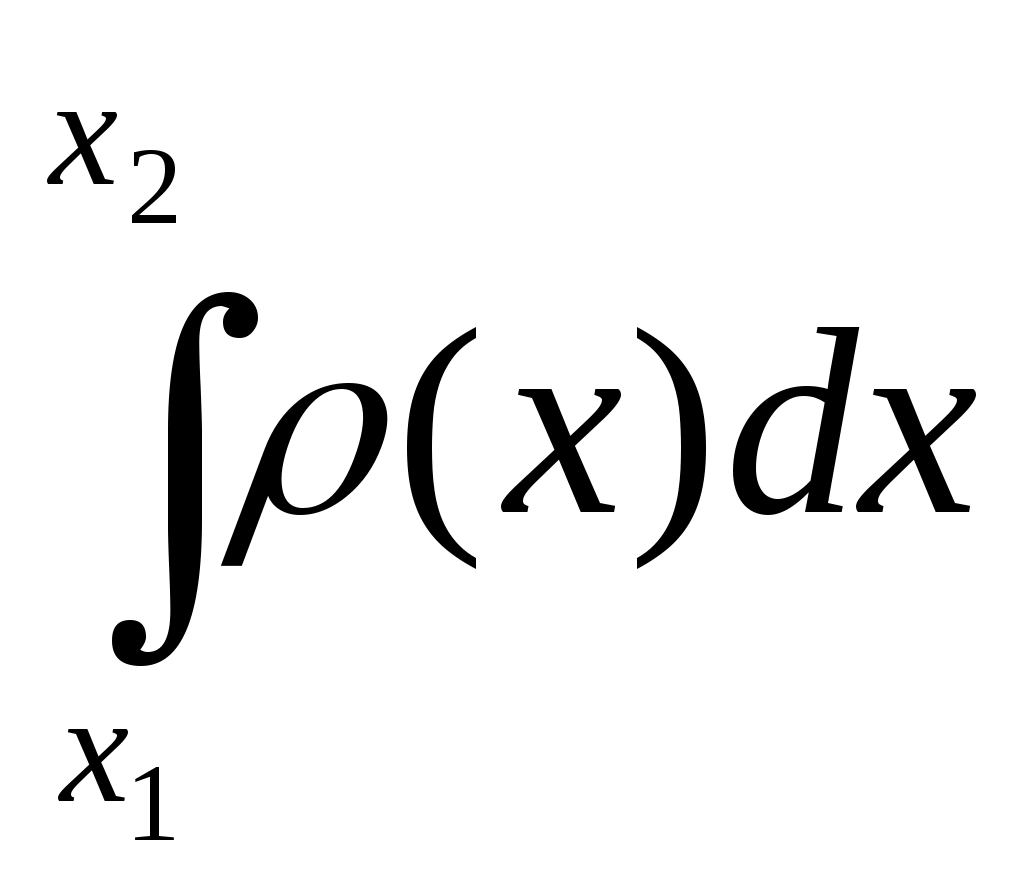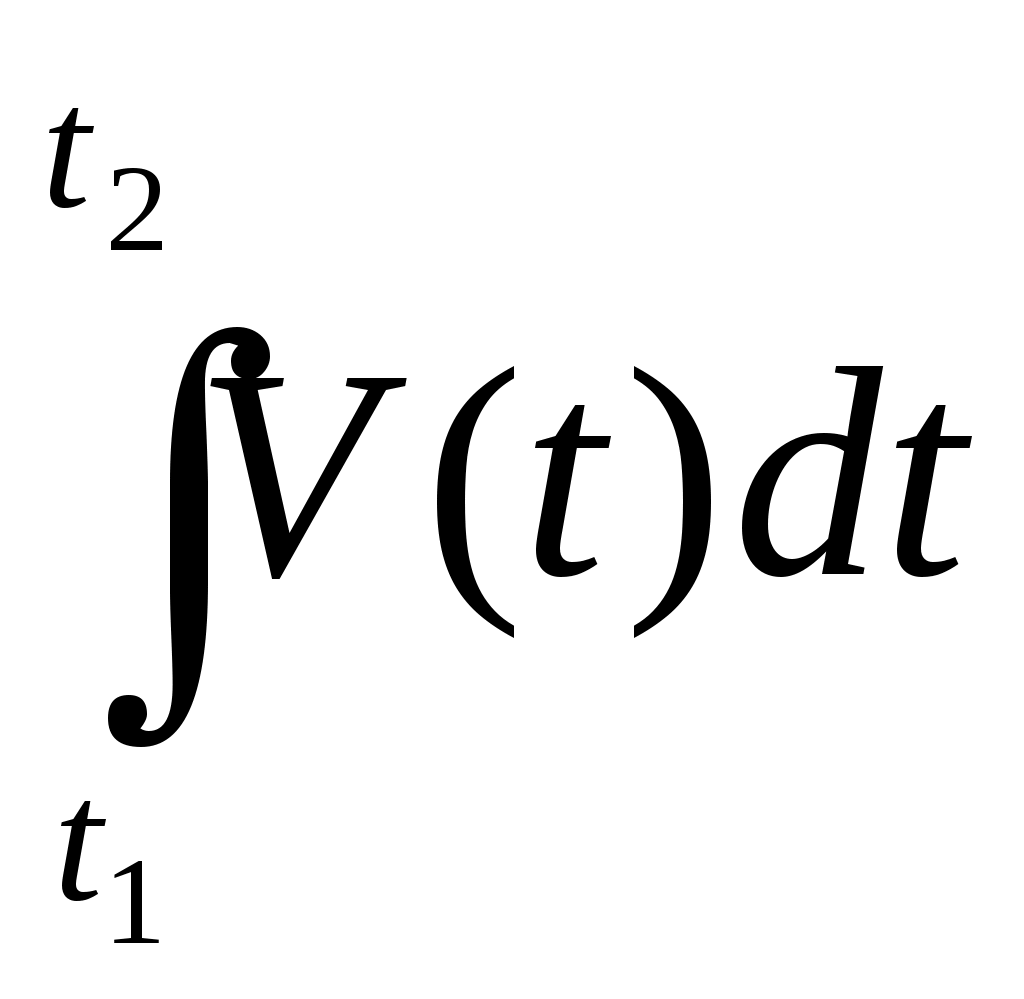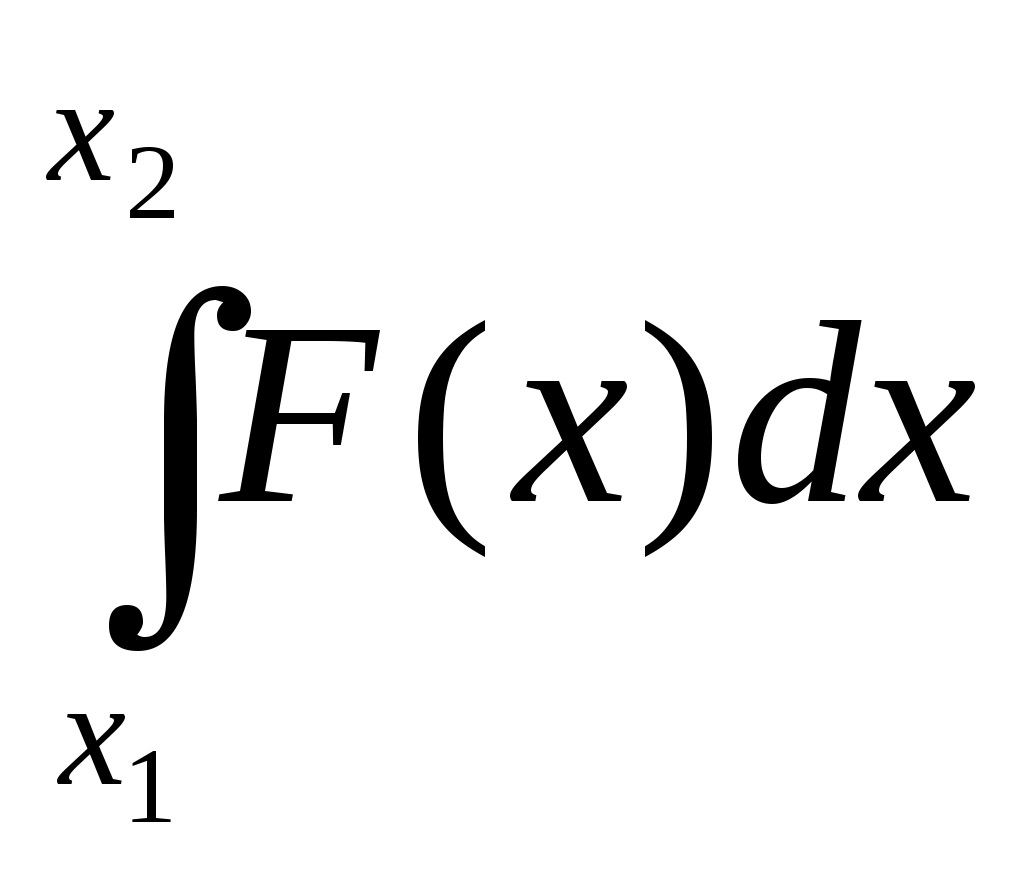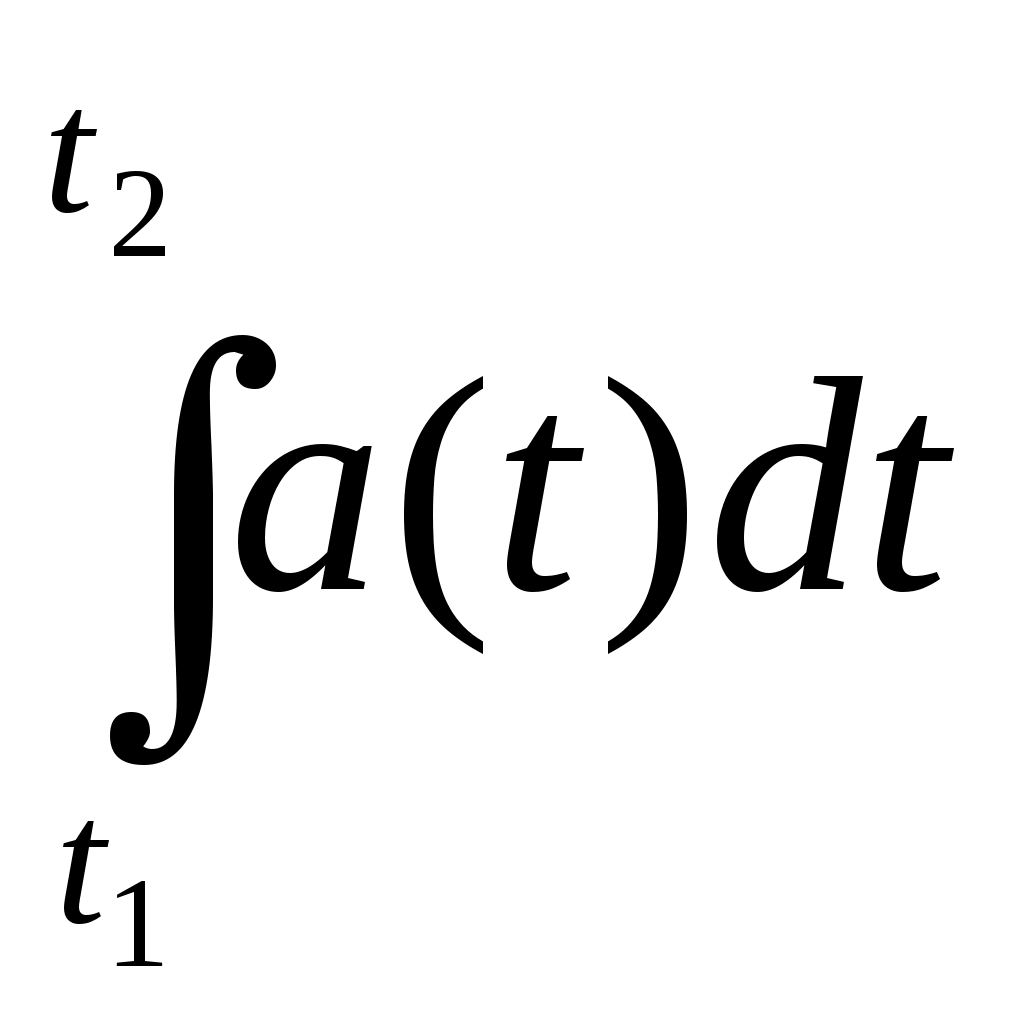Дипломная работа на тему _ обучение учащихся средней школы решен. Обучение учащихся средней школы решению задач на применение физического смысла производной и первообразной Дипломная работа
 Скачать 1.01 Mb.
|
|
Тренажер 1. Вычислите скорость изменения функции в указанной точке.
Тренажер 2. Задан закон прямолинейного движения точки x=x(t), t  [0;10].Найдите среднюю скорость движения на указанном отрезке времени. Найдите скорость и ускорение в момент времени t0. 3. Найдите моменты остановки. Продолжает ли точка после момента остановки двигаться в том же направлении или начинает движение в противоположном направлении?
«Приложения первообразной. Физический смысл первообразной» Определение: F(x) - первообразная для f(x) на множестве X если F'(x) = f(x) для всех х Х. Если F(x) - первообразная для f(x) на множестве X, то F(x) + с -множество всех первообразных для f(x) на множестве X. Это множество первообразных называют интегралом и обозначают  = F(x) + C.Вспомним пример из механики. Если в начальный момент времени t=0 скорость тела равна 0, т.е. V(0)=0, то при свободном падении тело к моменту времени t пройдет путь S(t) =  Эта формула была найдена Галилеем экспериментально. Дифференцированием находим скорость: S'(t) = V(t) = gt. Второе дифференцирование дает ускорение: V'(t) = a(t) = g, т.е. ускорение постоянно. Более типично для механики иное положение: известно ускорение точки a(t)(в нашем случае оно постоянно), требуется найти закон изменения скорости V(t), а также найти координату S(t). Иными словами, по заданной производной V'(t), равной a(t), надо найти V(t), а затем по производной S'(t), равной V(t), найти S(t). Для решения таких задач служит операция интегрирования и ее физический смысл. Чтобы сформулировать физический смысл первообразной рассмотрим ел едущую задачу: Дано: f(x) (скорость изменения физического процесса при данном значение аргумента (t, m, p...). Найти: Характеристику (величину самого процесса, зависящую от того же самого аргумента) при данном значение аргумента. Итак, первообразная функции у =f(x) в точке х0 показывает величину F(x0) если скорость изменения этого процесса в точке х0 равнаf(х0). В этом заключается физический смысл первообразной. При параллельном изучении основ механики и основ математического анализа открываются наибольшие возможности для формирования как физических понятий - мгновенная скорость, мгновенная ускорение, перемещение, работа и т. д., так и математических - производная, первообразная и интеграл. Для курса физики знание производной и интеграла открывает перспективы в плане возможности более строгого определения рода физических величин: точной записи второго закона Ньютона и закона электромагнитной индукции; получения формулы работы силы тяготения в сферически симметричном поле с последующим выводом второй космической скорости; ЭДС индукции, возникающей в рамке при вращении в магнитном поле; доказательства инвариантности действия сил относительно инерциальных систем отсчета; упрощения работы с графиками; и наконец, рассмотрения видов равновесия тел не только с позиций действия сил, но и с энергетической точки зрения. Знание учащимися производной и интеграла позволяет выработать у них общий подход к определению физических величин и решению графических задач физического содержания (см. табл.3) С этой целью можно, например, использовать алгоритмические схемы, являющиеся общими для определения математических и функциональных физических зависимостей. Так, для определения физического понятия с помощью интеграла можно избрать следующую схему действия: 1. Убедиться в возможности применения понятия «интеграл» в данной ситуации: приближенное значение искомой физической величины может быть представлена как сумма выражений  , где fi– некоторое среднее значение функции на промежутке ; графически эта сумма должнасоответствовать значению площади ступенчатой фигуры, а при  площадь должна сводится к площади криволинейной трапеции.Записать искомую физическую величину как  Сформулировать: определение найденной физической величины, определяемой как интеграл от данной функции; название функции; название аргумента. В большинстве случаев схема записи интеграла может быть иной. Поскольку интегрирование - это действие, обратное дифференцированию, применим следующий порядок действий: Записать производную искомой функции по соответствующему аргументу, например - V= dx/dt. Определить функцию, от которой была найдена производная, то есть первообразную х =  .3. Найти изменение искомой функции при соответствующих значениях аргумента: t1и t2, то есть интеграл х2 – х1 =  , после чего сформулировать определение физической величины.Преимущества, которые дает знание производной и интеграла для изучения курса физики в 9 - 11 классах, могут быть получены только в результате совместной работы над формированием понятий математического анализа на уроках математики и физики.
Табл.3. Приложение интеграла Пример 1. Материальная точка массой 2 кг движется по оси Ох под действием силы, направленной вдоль этой оси. В момент времени t эта сила равна F(t)=3t-2. Найдите закон x(t) движения точки, если известно, что при t=2c скорость точки равна 3 м/с, а координата равна 1 (F-сила в Ньютонах, t-время в секундах, х -путь в метрах). Решение. Согласно второму закону Ньютона F = та, где а- ускорение. Имеем  Воспользуемся физическим смыслом первообразной.  Постоянную С, находим из условия V(2) = 3:  и  Постоянную  находим из условия х(2)=1: Итак, закон движения точки: Пример 2. Найти статические моменты и моменты инерции относительно осей Ох и Оу дуги цепной линии y=chx при 0≤x≤1. 1) Всюду в задачах, где плотность не указана, предполагается, что кривая однородна и  =1.Решение: Имеем: 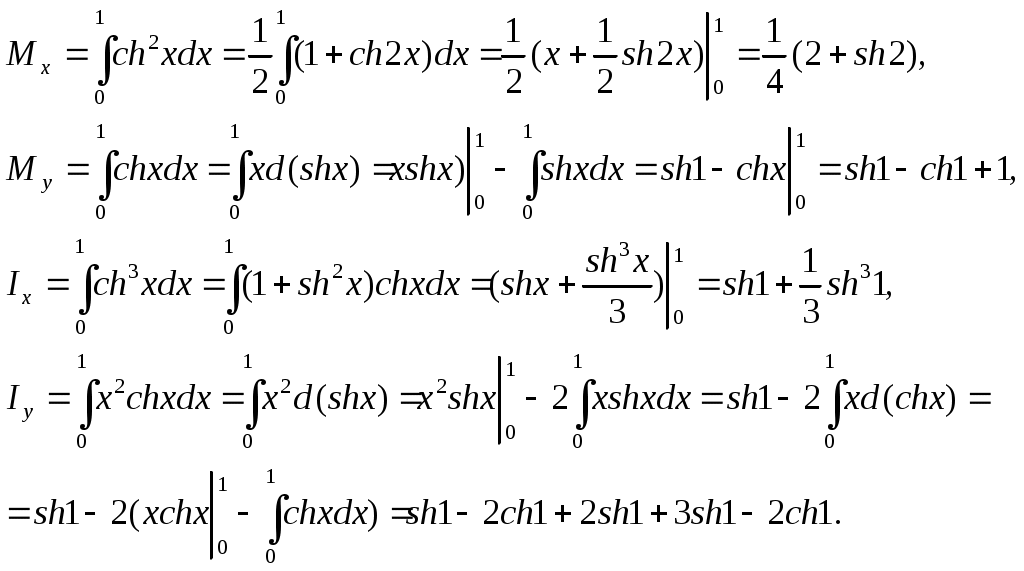 Следовательно, Пример 3. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти. Решение: Имеем:  Отсюда получаем: Пример 4. Скорость прямолинейного движения тела выражается формулой  (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.Решение: Так как путь, пройденный телом со скоростью 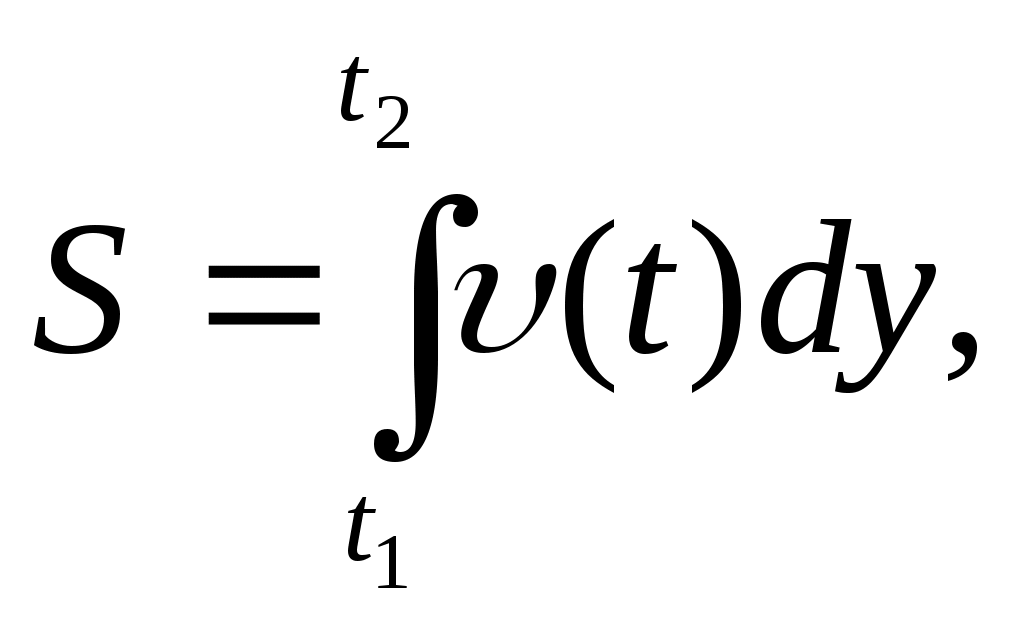 (t) за отрезок времени [t1,t2], выражается интегралом то имеем:  Задачи для закрепления темы: 1.Скорость прямолинейно движущейся точки задана формулой V(t) = t2 + 2t-1. Запишите формулу зависимости ее координаты х от времени t, если известно, что в начальный момент времени (t=0) точка находилась в начале координат. 2.Скорость Прямолинейно движущейся точки задана формулой  Найдите формулу, выражающую зависимость координаты точки от времени, если известно, что в момент  точка находилась на расстояние 4 м от начала координат.3.Точка движется прямолинейно с ускорением a(t)= 12t2 +4. Найдите закон движения точки, если в момент t=lc ее скорость равна 10 м/с, а координата равна 12 (единица измерения а равна 1 м/с2). Материальная точка массой m движется по оси Ох под действием силы, направленной вдоль этой оси. В момент времени t эта сила равна F(t). Найдите формулу зависимости x(t) от времени t, если известно, что при t = t0скорость точки равна V0а координата равна х0 (F-сила в Ньютонах, t-время в секундах, v -путь в метрах, m - в килограммах). а) F(t) = 6-9t,t0 =l,V0= 4,х0 =-5,m= 3 б)  Вычислите массу участка стержня от х,=1 до х2=2, если его линейная плотность задается формулой  (х)= 4х3 + 5х + 2.Вычислите количество электричества, протекающего по проводнику за промежуток времени [2;3] , если сила тока задается формулой I(t) = 3t2 -2t + 5 7. Вычислите работу, затраченную при сжатии винтовой пружины на 6 см, если коэффициент сжатия равен  .Вычислите работу за промежуток времени [4;9], если мощность вычисляется по формуле N(t) = 6  .Вычислите работу по переносу единичной массы, совершенную силой F(x)= 6х2 + 4х - 2 на участке [-1 ;2] Вычислите работу, затраченную при растяжение каучукового шнура на 20 см, если коэффициент растяжения равен 0,008 Какую работу необходимо затратить для того, чтобы тело массы m поднять с поверхности Земли, радиус которой R, на высоту һ? Чему равна работа, если тело удаляется в бесконечность? На прямой расположены материальная точка массы m и однородный стержень массы M и длины l. Точка удалена от концов стержня на расстояния c и c+l. Определить силу гравитационного притяжения между стержнем и точкой. Вычислить кинетическую энергию диска массы М и радиуса R, вращающегося с угловой скоростью щ около оси, проходящей через его центр перпендикулярно к его плоскости. Стержень АВ вращается в горизонтальной плоскости вокруг оси ОО' с угловой скоростью щ=10р рад/с. По-перечное сечение стержня S = 4 см2, длина его l = 20 см, плотность материала, из которого он изготовлен, г= 7,8 * 103 кг/м3. Найти кинетическую энергию стержня. Треугольная пластинка, основание которой а = 40 см, а высота h = 30 см, вращается вокруг своего основания с постоянной угловой скоростью  =5р рад/с. Найти кинетическую энергию пластинки, если толщина ее d = 0,2 см, а плотность материала, из которого она изготовлена, г= 2,2 * 103 кг/м .Найти давление воды на плотину, если вода доходит до её верхнего края и если известно, что плотина имеет вид трапеции с высотой h, верхним основанием а и нижним основанием b. Вычислить силу давления воды на вертикальную плотину, имеющую форму трапеции, верхнее основание которой равно 70 м, нижнее 50 м, а высота 20 м. Найдите работу переменного тока, изменяющегося по формуле за промежуток времени , если сопротивление цепи равно R. Два точечных электрических заряда +10-4 и -10-4 Кл находятся на расстоянии 10 см друг от друга. Найдите работу, необходимую для того, чтобы развести их на расстояние 10 км. Какую работу требуется выполнить, чтобы с помощью ракеты тело массы m поднять с поверхности Земли, радиус которой R, на высоту h? Найти работу, выполняемую при переносе материальной точки, имеющей массу m, из A(a) в B(b), если притягивающая её по закону Ньютона точка имеет массу м и находится в начале координат. Из цистерны, имеющей форму прямого кругового конуса радиусом основания R и высотой H, выкачивают воду через вершину конуса. Найдите совершаемую при этом работу. Найдите числовое значение работы при R=3 м, H=5 м, считая плотность воды с=1 г/см .Тренажер 1. Вычислите перемещение точки за указанный промежуток времени  позаданной скорости V= V(t)
Тест. Применение интеграла в физике Найдите правильные формулы, которые связывают следующие физические величины: А-работа, S-перемещение,V-скорость,m-масса,t-время, а- ускорение,I-сила тока, х- координата, Р- сила, -плотность, q-заряд.
Самостоятельная работа. Физические приложения интеграла. На рисунке изображен график изменения скорости точки, движущийся прямолинейно. а) какой путь точка проходит за промежуток времени ?б) найдите закон изменения координаты х=х(t),зная, что х(0)=1, и постройте график функции x=x(t).  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||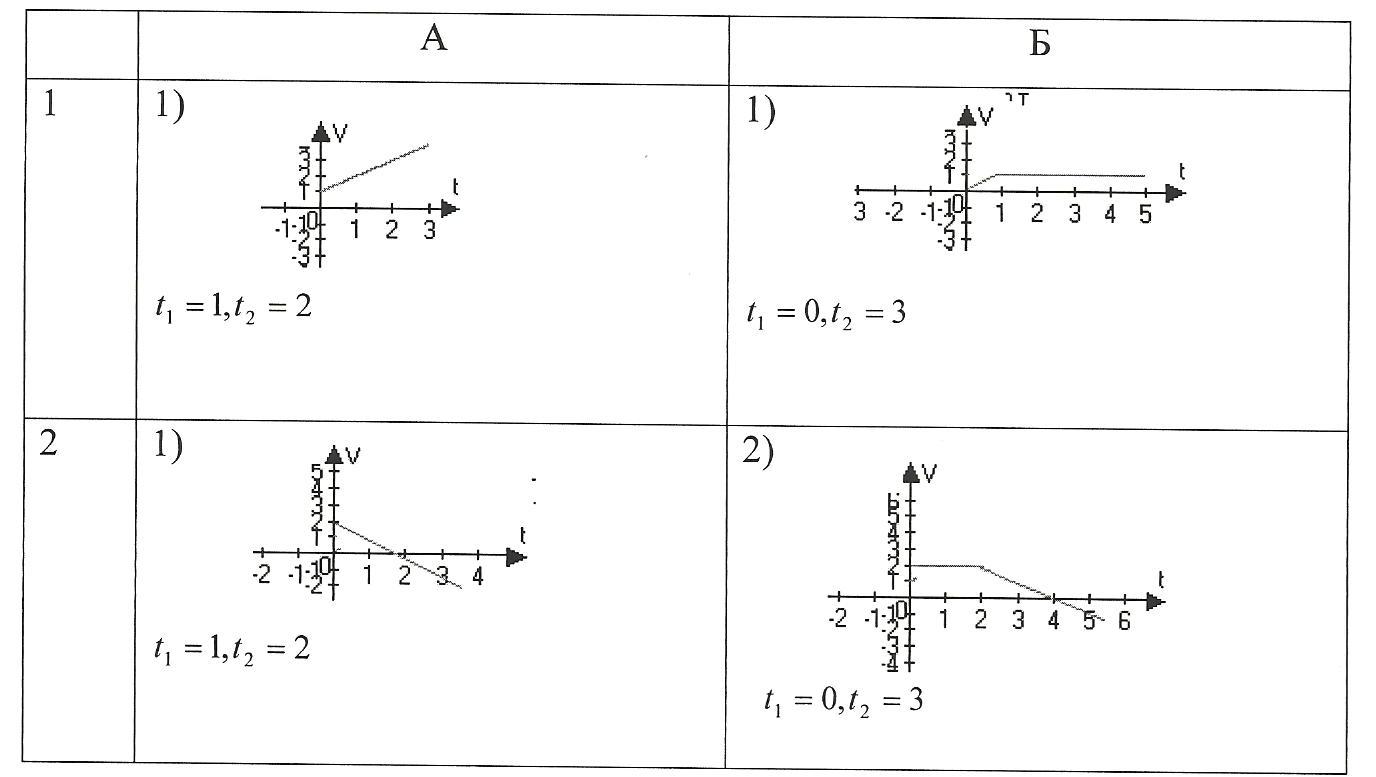
,t0=2
+2,t0=0,5
,t0=1
-2,t1=0,t2 =1
