Механика. МЕХАНИКА. Одержание Кинематика поступательного и вращательного движения 5 Динамика поступательного и вращательного движений 11 Механические колебания и волны 21 Молекулярная физика и термодинамика 31 введение
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
3. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ 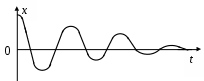 1. На рисунке приведен график зависимости смещения колеблющейся точки от времени, уравнение, его описывающее имеет вид 1. 4. 2 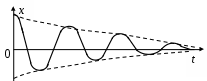 . На рисунке приведены графики зависимости смещения колеблющейся точки и амплитуды колебания от времени. Амплитуда колебания меняется по закону . На рисунке приведены графики зависимости смещения колеблющейся точки и амплитуды колебания от времени. Амплитуда колебания меняется по закону1. 4. 3. Логарифмический декремент затухания – это физическая величина, показывающая во сколько раз уменьшается амплитуда колебаний за период обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается до нуля обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается в «е» раз обратная промежутку времени, за которое амплитуда колебаний уменьшается в «е» раз обратная промежутку времени, за которое амплитуда колебаний уменьшается до нуля 4. Точка совершает колебание по закону 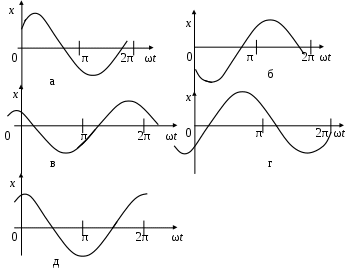 1. а 2. б 3. в 4. г 5. д 5 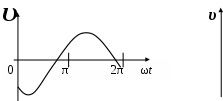 . Точка совершает колебание по закону . Точка совершает колебание по закону 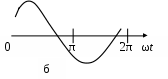 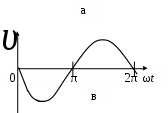 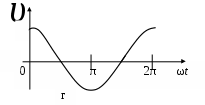 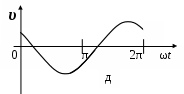 1. а 2. б 3. в 4. г 5. д 6. Точка совершает колебание по закону 1. А 2. Аω 3. Аω2 4. А2ω2 5. ускорение – постоянная величина 7. Если точка участвует в двух взаимно перпендикулярных колебаниях, происходящих по закону  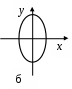 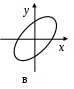 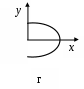 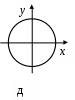 1. а, б, д 2. б, в, д 3. а, б, в, г 4. а, б, в, г, д 5. а, б, в, д 8. Если точка участвует в двух взаимно перпендикулярных колебаниях одинаковой частоты, происходящих по закону 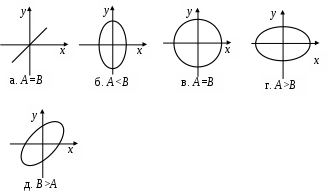 1. а, б, в, г, д 2. в, г, д 3. в, г 4. б, в, г 5. а, в, г 9. Точка совершает колебание по закону 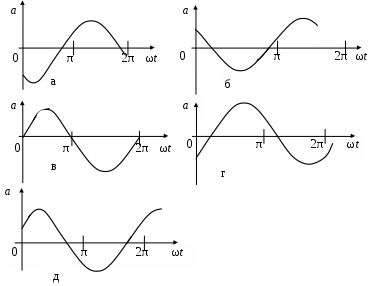 1. а 2. б 3. в 4. г 5. д 10. Если на расстоянии х1 и х2 от положения равновесия частица, совершающая гармонические колебания, имеет скорости равные соответственные υ1 и υ2 , то амплитуда колебаний равна 1. 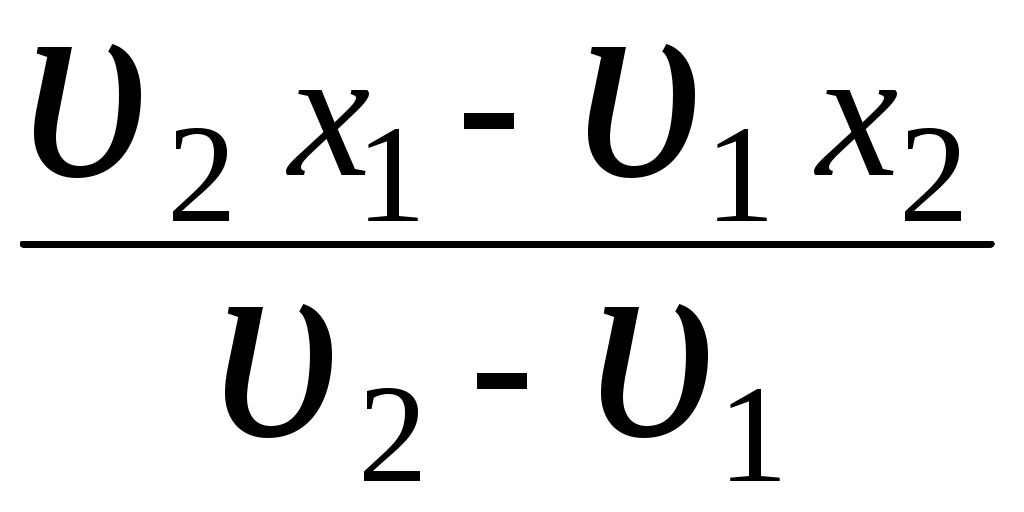 2. 2. 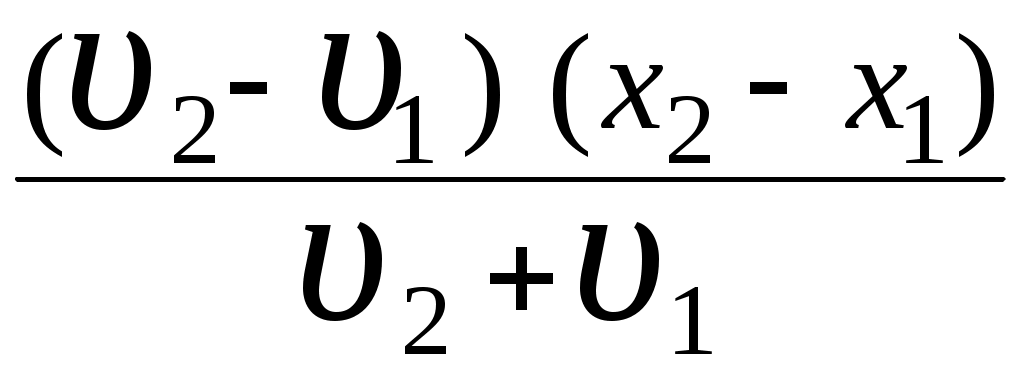 3. 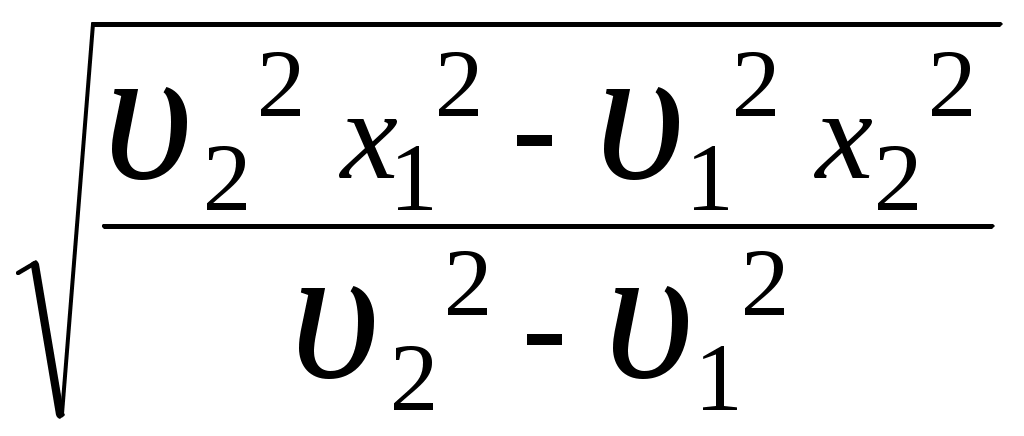 4. 4. 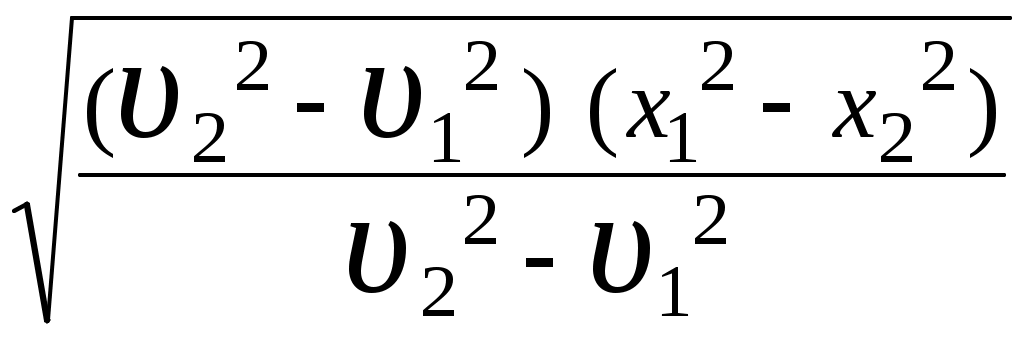 5. данных для определения амплитуды недостаточно 11. За 10 с амплитуда пружинного маятника массой m = 0,1 кг уменьшилась в «е» раз. Коэффициент затухания β и коэффициент сопротивления r среды равны 1. β = 0,1; r = 0,02 2. β = 1; r = 0,01 3. β = 0,1; r = 0,1 4. β = 0,01; r = 0,04 5. β = 1/2,73; r = 0,02 12. Фигура Лиссажу, образованная при сложении взаимно перпендикулярных колебаний 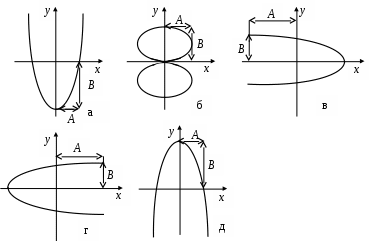 1. а 2. б 3. в 4. г 5. д 13. Период колебаний математического маятника можно уменьшить увеличив амплитуду колебаний увеличив массу маятника удлинив нить подвеса укоротив нить подвеса уменьшив амплитуду колебаний 14. Коэффициент затухания колебаний маятника можно увеличить уменьшив вязкость среды, в которой происходит колебание уменьшив массу колеблющегося тела уменьшив начальную амплитуду колебаний увеличив массу колеблющегося тела уменьшив начальную амплитуду колебаний и вязкость среды 15. Уравнение гармонических колебаний материальной точки 1. 6,0 2. 4,0 3. 2,0 4. 1,0 5. 8,0 16. Уравнение гармонического колебания 1. 4. 17. Амплитуда гармонических колебаний, совершаемых материальной точкой вдоль прямой, равна 0,5 м. Путь, пройденный точкой за период колебаний, равен (м) 1. 2 2. 1,5 3. 1 4. 0,5 5. 0 18. Максимальная скорость гармонического осциллятора 10 см/с, максимальное ускорение 1 м/с2. Период колебаний равен (с) 1. 10 2. 6,28 3. 4 4. 3,14 5. 0,628 19. Небольшое тело на нити совершает колебания как математический маятник. Ускорение тела равно нулю в следующих точках траектории 1. в двух крайних и в положении равновесия 2. только в положении равновесия 3. только в крайних точках 4. зависит от амплитуды 5. ни в одной 20. Небольшое тело на нити совершает колебания как математический маятник. Сила, действующая на тело равна нулю в следующих точках траектории 1. в положении равновесия (нижней точке) 2. в крайних точках 3. и в положении равновесия, и в крайних точках 4. ни в одной точке 5. зависит от массы тела 21. Математический маятник совершает колебания по закону х = 0,004 cos (2t + 0,8) (м). Длина маятника равна (м) 1. 4 2. 3,25 3. 0,245 4. 2,45 5. 2,05 22. Колебание точки задано уравнением х = 2sin 2,5π (t+0,4). Период колебаний равен (с) 1. 2 2. 1 3. 0,8 4. 0,6 5. 0,4 23. Точка совершает гармонические колебания. Наибольшее смещение точки 10 см, наибольшая скорость 0,2 м/с. Максимальное ускорение точки равно (м/с2) 1. 2 2. 0,2 3. 0,3 4. 0,4 5. 0.04 24. Уравнение колебания материальной точки имеет вид 1. 4. 25. Материальная точка массой 1,25 кг совершает колебания по закону х = cos (2t+ π/4) 1. 2,5 2. 5 3. 0,98 4. 3,5 5. 1 26. Тело массой 1 кг совершает колебания вдоль оси х. Его координата изменяется по закону х =2sin 3t. Потенциальная энергия тела определяется выражением 1. 4. 27. Точка совершает гармонические колебания согласно уравнению х = 0,04 sin (π t+ 0,3π) (м). Максимальная сила, действующая на точку, равна 1,5 мН. Полная энергия точки (мкДж) равна 1. 60 2. 30 3. 15 4. 12 5. среди ответов нет правильного 28. Материальная точка совершает колебания по закону х = А sin ωt. В некоторый момент времени смещение точки оказалось равным 5 см. Когда фаза увеличилась в 2 раза, смещение стало равным 8 см. Амплитуда колебаний равна (см) 1. 8,33 2. 4,16 3. 3 4. 2,5 5. 2,31 29. Однородный тонкий стержень длиной lсовершает колебания около горизонтальной оси, проходящей через конец стержня. Период колебаний равен 1. 30. Диск радиуса R колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Период его колебаний пропорционален 1. 31. Диск радиусом 24 см колеблется около оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Приведенная длина маятника равна (см) 1. 12 2. 14 3. 16 4. 28 5. 36 32. Уравнение колебаний физического маятника массой 0,2 кг и моментом инерции 0,4 кг·м2 определяется выражением х = 2 cos 5 t(м). Расстояние от центра масс до точки подвеса равно (м) 1. 0,4 2. (0,4)0,5 3. 5 4. 4 5. 2 33. Складываются два гармонических колебания одного направления с одинаковыми периодами (1,5 с) и амплитудами А1=А2=2 см. Начальные фазы колебаний 1. arctg 2 2. arctg 0,28 3. arctg 3,7 4. π/6 5. 5π/6 34. Уравнение бегущей вдоль оси х волны имеет вид 1. 35. Волна с периодом 1,2 с и амплитудой 2 см распространяется со скоростью 15 м/с. Точка находится на расстоянии 45 м от источника волн. В момент t = 4 с смещение точки равно (м) 1. 0,01 2. 0,06 3. 0,02 4. 0,1 5. 0 36. Уравнение стоячей волны определяется соотношением 1. 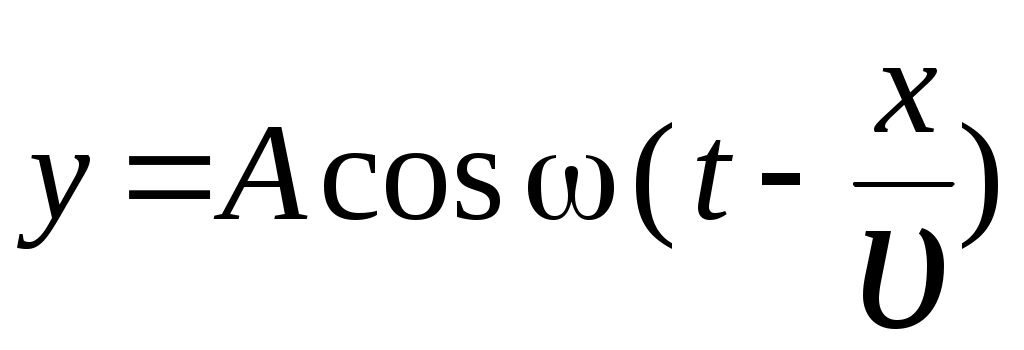 2. 2. 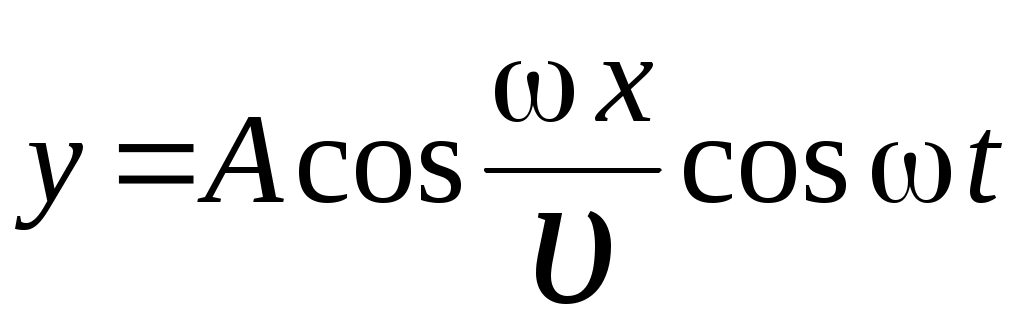 3. 3. 37. Расстояние между первым и третьим узлами в стоячей волне равно 20 см. Длина волны равна (м) 1. 0,8 2. 0,6 3. 0,4 4. 0,2 5. надо знать скорость распространения волны 38. Расстояния между соседними точками, колеблющимися с одинаковыми по величине амплитудами равны 5 см и 15 см. Длина стоячей волны (м) 1. 0,8 2. 0,4 3. 0,2 4. 0,15. 5. данных недостаточно 39. Груз массой 1 кг, подвешенный на пружине, растягивает ее на 20 см. Если оттянуть немного груз и отпустить, то возникнут колебания, период которых равен (с) 1. 0,7 2. 0,9 3. 1,1 4. 1,3 5. 1,8 40. Математический маятник длиной 1 м установлен в лифте, опускающимся вниз с ускорением 2,5 м/с2. Период колебания маятника равен (с) 1. 1,6 2. 1,8 3. 2 4. 2,3 5. данных недостаточно 41. Колебания двух точек, лежащих на луче и отстоящих на расстоянии 2 м друг от друга, если длина волны равна 1 м происходят в одинаковых фазах, происходят в противофазах сдвинуты по фазе на сдвинуты по фазе на происходят в одинаковых фазах, 42. За одно полное колебание амплитуда колебаний математического маятника с логарифмическим декрементом затухания 0,3 уменьшится в 1. «е» раз 2. 1,35 раз 3. 1,22 раза 4. 2 раза 5. 3 раза |
