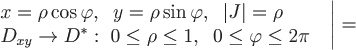|
|
Определение. Числовая функция, заданная в каждой точке некоторой пространственной области, называется скалярным полем
Пример 2. Определить векторные линии магнитного поля, образованного постоянным электрическим током с силой 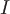 , текущим по бесконечно длинному прямолинейному проводу. , текущим по бесконечно длинному прямолинейному проводу.
Решение.
Если принять провод за ось 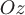 , то вектор , то вектор 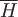 напряженности магнитного поля выражается формулой напряженности магнитного поля выражается формулой
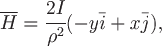 где где 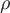 - расстояние от произвольной точки - расстояние от произвольной точки 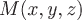 до провода. до провода.
В данном случае 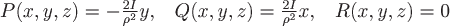 . .
Поэтому дифференциальные уравнения векторных линий примут вид:
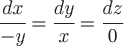 , ,
здесь сократили на общий множитель 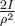 . .
Последняя система равносильна системе
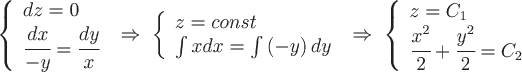
Значит, векторные линии напряженности магнитного поля определяются уравнениями 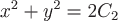 и и  , где , где 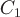 и и 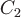 - константы. Эти линии являются окружностями с центрами на оси - константы. Эти линии являются окружностями с центрами на оси 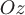 , лежащими в плоскостях, перпендикулярных этой оси. , лежащими в плоскостях, перпендикулярных этой оси.
Вопрос. Векторными линиями векторного поля 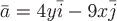 являются являются
семейство гипербол 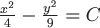
семейство прямых 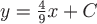
семейство эллипсов 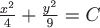
семейство парабол 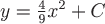
Поток векторного поля
Пусть в поле вектора 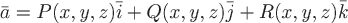 задана ориентированная поверхность задана ориентированная поверхность  . Обозначим через . Обозначим через 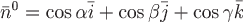 единичный вектор нормали к выбранной стороне поверхности в ее произвольной точке. единичный вектор нормали к выбранной стороне поверхности в ее произвольной точке.
Если для наглядности считать, что вектор  - вектор скорости несжимаемой жидкости, движущейся стационарно, а поверхность - вектор скорости несжимаемой жидкости, движущейся стационарно, а поверхность  находится в этой жидкости. Подсчитаем количество жидкости, протекающей через эту поверхность за единицу времени. находится в этой жидкости. Подсчитаем количество жидкости, протекающей через эту поверхность за единицу времени.
Для этого разобьем поверхность  на на  элементарных поверхностей элементарных поверхностей 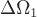 , , 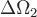 , ..., , ..., 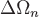 . В каждой из этих поверхностей . В каждой из этих поверхностей 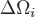 выберем точку выберем точку 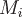 , отложим от нее вектор нормали , отложим от нее вектор нормали 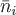 . Условимся при этом, что если . Условимся при этом, что если  замкнутая поверхность, то замкнутая поверхность, то 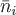 берется по направлению внешней нормали. Если же берется по направлению внешней нормали. Если же  незамкнута, то выберем произвольно направление нормалей так, чтобы они лежали по одну сторону от поверхности. Поверхности незамкнута, то выберем произвольно направление нормалей так, чтобы они лежали по одну сторону от поверхности. Поверхности 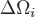 в силу их малости можно считать плоскими, а вектор в силу их малости можно считать плоскими, а вектор  постоянным во всех точках постоянным во всех точках 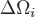 и равным и равным 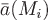 . .
Поэтому количество жидкости 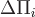 , протекающей через поверхность , протекающей через поверхность 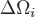 , будет приблизительно равно объему цилиндрической фигуры с основанием , будет приблизительно равно объему цилиндрической фигуры с основанием 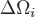 и и образующей и и образующей 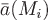 , т.е. , т.е.
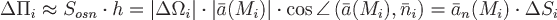 , ,
где 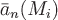 - проекция вектора - проекция вектора 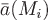 на нормаль на нормаль 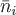 и и 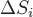 - площадь поверхности - площадь поверхности 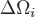 . .
Общее количество жидкости 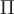 , протекающей через поверхность , протекающей через поверхность  в единицу времени, равно сумме количеств жидкости, протекающей через все элементарные поверхности. Поэтому будем иметь: в единицу времени, равно сумме количеств жидкости, протекающей через все элементарные поверхности. Поэтому будем иметь:
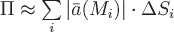
Если существует предел полученных интегральных сумм при неограниченном увеличении числа элементов разбиения поверхности  и при стремлении диаметра разбиения (т.е. наибольшего размера поверхностей, входящих в разбиение) к нулю, то он является поверхностным интегралом функции и при стремлении диаметра разбиения (т.е. наибольшего размера поверхностей, входящих в разбиение) к нулю, то он является поверхностным интегралом функции 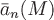 по поверхности по поверхности  и обозначается и обозначается 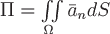 . .
Определение. Поверхностный интеграл 1 рода по поверхности  от скалярного произведения вектора от скалярного произведения вектора  на вектор на вектор 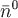 называется потоком векторного поля через ориентированную поверхность называется потоком векторного поля через ориентированную поверхность  и обозначается и обозначается 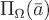 : :
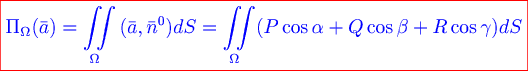
В случае замкнутой поверхности  поток записывается в виде поток записывается в виде 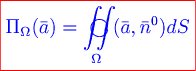 . .
Если ввести в рассмотрение вектор 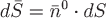 и обозначить его проекции на оси координат и обозначить его проекции на оси координат 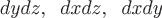 , то формулу для потока можно переписать в виде , то формулу для потока можно переписать в виде
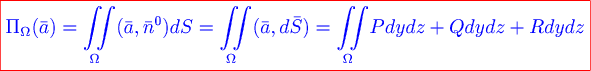 , ,
где вектор 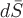 направлен по нормали к выбранной стороне поверхности направлен по нормали к выбранной стороне поверхности  . Правая часть последнего равенства является поверхностным интегралом 2 рода. . Правая часть последнего равенства является поверхностным интегралом 2 рода.
Если, например,  – поле скоростей текущей жидкости в области – поле скоростей текущей жидкости в области  и и  – незамкнутая поверхность с выбранным направлением нормали – незамкнутая поверхность с выбранным направлением нормали 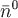 , то поток , то поток 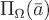 равен количеству жидкости, проходящей в единицу времени через поверхность равен количеству жидкости, проходящей в единицу времени через поверхность  в направлении вектора в направлении вектора 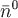 . Если . Если  – замкнутая поверхность, ограничивающая некоторую область – замкнутая поверхность, ограничивающая некоторую область 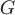 с внешней нормалью с внешней нормалью 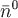 , то поток , то поток 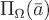 равен разности количеств втекающей в эту область жидкости и вытекающей. В случае, если поток равен разности количеств втекающей в эту область жидкости и вытекающей. В случае, если поток 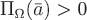 , то в области , то в области 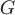 имеются источники (где векторные линии порождаются), а если имеются источники (где векторные линии порождаются), а если 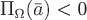 , то это указывает на наличие в области , то это указывает на наличие в области 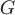 стоков (где векторные линии заканчиваются). А если стоков (где векторные линии заканчиваются). А если 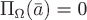 , тогда либо нет ни источников ни стоков, либо источники и стоки уравновешивают друг друга. , тогда либо нет ни источников ни стоков, либо источники и стоки уравновешивают друг друга.
Если ориентированная поверхность  задана явно непрерывно дифференцируемой функцией задана явно непрерывно дифференцируемой функцией 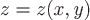 , где , где 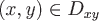 , то можно получить следующую формулу, связывающую поверхностный интеграл по поверхности , то можно получить следующую формулу, связывающую поверхностный интеграл по поверхности  с двойным интегралом по проекции с двойным интегралом по проекции 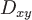 этой поверхности на плоскость этой поверхности на плоскость 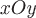 : :
 , ,
где знак «плюс» берется, когда угол 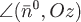 острый. острый.
Если поверхность  задана явно уравнением задана явно уравнением 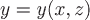 , где , где 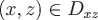 или или 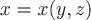 , где , где 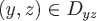 , то соответственно меняются роли переменных в последней формуле. , то соответственно меняются роли переменных в последней формуле.
Пример. Найти поток векторного поля 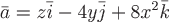 через часть поверхности параболоида через часть поверхности параболоида 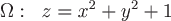 , отсеченной плоскостью , отсеченной плоскостью  , если нормаль , если нормаль 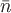 к заданной поверхности составляет тупой угол с осью аппликат. к заданной поверхности составляет тупой угол с осью аппликат.
Решение.
Поток векторного поля  будем искать по формуле будем искать по формуле 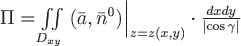 , где , где 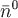 – единичный вектор нормали к заданной поверхности – единичный вектор нормали к заданной поверхности  , угол , угол 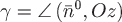 , область , область 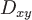 – проекция поверхности – проекция поверхности  на плоскость на плоскость 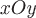 . .
Для поверхности 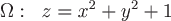 или или 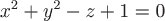 нормаль нормаль 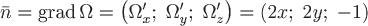 , тогда единичный вектор нормали , тогда единичный вектор нормали 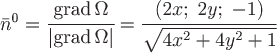 , В данном случае , В данном случае  , т.е. , т.е. 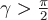 (тупой угол). (тупой угол).
Найдем скалярное произведение 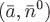 : :
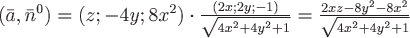 . .
Т.к. проекцией заданной поверхности  на плоскость на плоскость  является круг радиуса является круг радиуса  (потому что (потому что 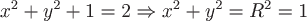 ), то при вычислении соответствующего двойного интеграла необходимо будет перейти в ПСК (полярную систему координат). ), то при вычислении соответствующего двойного интеграла необходимо будет перейти в ПСК (полярную систему координат).
Вычислим требуемый поток векторного поля:
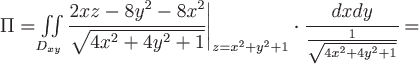
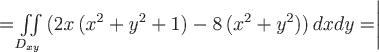 ПСК ПСК 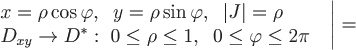
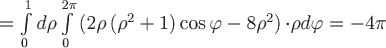 . .
|
|
|
 Скачать 0.77 Mb.
Скачать 0.77 Mb.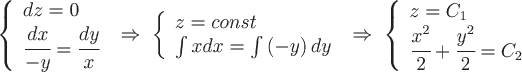
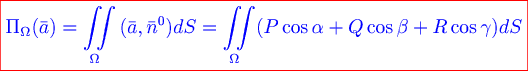
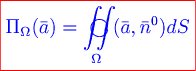 .
.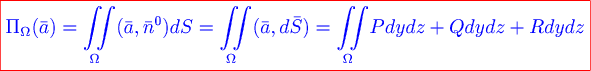 ,
,  ,
,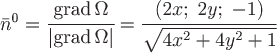 , В данном случае
, В данном случае 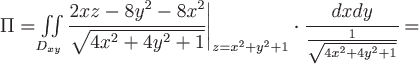
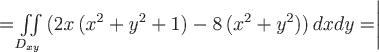 ПСК
ПСК