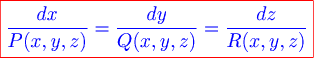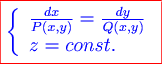|
|
Определение. Числовая функция, заданная в каждой точке некоторой пространственной области, называется скалярным полем
Свойства градиента.
1) 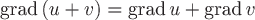 , ,
т.е. градиент алгебраической суммы скалярных полей 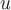 и и 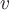 есть сумма градиентов указанных полей. Это свойство непосредственно вытекает из определения градиента, т.к. производная суммы равна сумме производных. есть сумма градиентов указанных полей. Это свойство непосредственно вытекает из определения градиента, т.к. производная суммы равна сумме производных.
2) Градиент произведения скалярных полей  . .
В правой части последнего равенства стоит сумма векторов, где 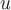 и и 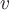 - скалярные множители. - скалярные множители.
3) 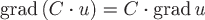 , где , где 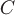 - постоянное произвольное число, - постоянное произвольное число,
т.е. постоянный множитель можно выносить за знак градиента.
4) Градиент частного скалярных полей 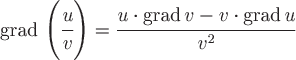 . .
5) Градиент сложной функции 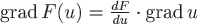 . .
В правых частях всех свойств знаки  и и  обозначают сложение и вычитание векторов, а знак произведения - есть произведение вектора на скаляр. обозначают сложение и вычитание векторов, а знак произведения - есть произведение вектора на скаляр.
Пример 3. Найти градиент потенциала электростатического поля, образованного точечным зарядом, помещенным в начало координат:
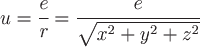 , где , где 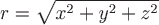 . .
Решение.
Для нахождения градиента будем использовать формулу 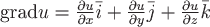 . .
Найдем проекции градиента, т.е. частные производные скалярного поля:
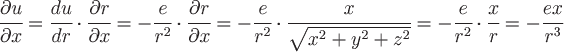 . .
Аналогично можно найти 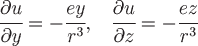 . .
Поэтому искомый градиент будет равен:
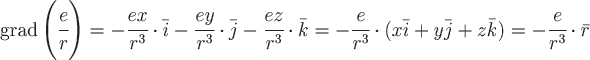 , где , где 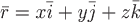 есть радиус-вектор произвольной точки пространства. есть радиус-вектор произвольной точки пространства.
Знак "минус" говорит о том, что градиент потенциала электростатического поля направлен противоположно радиус-вектору произвольной точки поля. Т.к. поверхностями уровня поля 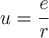 являются концентрические сферы, а нормаль сферы совпадает с ее радиусом, то градиент являются концентрические сферы, а нормаль сферы совпадает с ее радиусом, то градиент 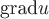 направлен по радиусу сферы к ее центру. направлен по радиусу сферы к ее центру.
Вопрос. Максимальное значение производной по направлению скалярного поля 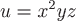 в точке в точке  равно равно
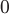
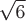
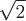
Виды скалярных полей
Во многих физических задачах приходится иметь дело с полями, обладающими теми или иными специальными свойствами симметрии, облегчающими изучение таких полей. Укажем некоторые частные случаи.
Плоскопараллельное поле
Если скалярное поле 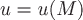 в какой-либо декартовой системе координат можно описать функцией, зависящей не от трех, а от двух координат, т.е. в какой-либо декартовой системе координат можно описать функцией, зависящей не от трех, а от двух координат, т.е. 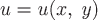 , то такое поле называется плоскопараллельным (или двумерным). , то такое поле называется плоскопараллельным (или двумерным).
Т.е. поле 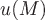 будет плоскопараллельным, если в пространстве существует направление, при сдвигах вдоль которого поле будет плоскопараллельным, если в пространстве существует направление, при сдвигах вдоль которого поле 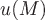 переходит само в себя. Поверхности уровня такого поля - это семейство цилиндрических поверхностей, причем в соответствующим образом выбранной системе координат они задаются уравнениями вида переходит само в себя. Поверхности уровня такого поля - это семейство цилиндрических поверхностей, причем в соответствующим образом выбранной системе координат они задаются уравнениями вида 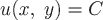 , где , где 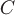 - произвольное число. - произвольное число.
Осесимметрическое поле
Если для поля 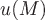 можно подобрать такую цилиндрическую систему координат, в которой оно изображается функцией, зависящей только от переменных можно подобрать такую цилиндрическую систему координат, в которой оно изображается функцией, зависящей только от переменных 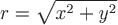 и и 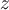 , но не от угла , но не от угла 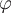 , то это поле называется осесимметрическим. , то это поле называется осесимметрическим.
Иначе говоря, поле 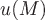 является осесимметрическим, если оно переходит само в себя при повороте пространства на произвольный угол вокруг некоторой фиксированной прямой - оси симметрии этого поля. Поверхности уровня такого поля представляют собой поверхности вращения. является осесимметрическим, если оно переходит само в себя при повороте пространства на произвольный угол вокруг некоторой фиксированной прямой - оси симметрии этого поля. Поверхности уровня такого поля представляют собой поверхности вращения.
Если эти поверхности вращения - круглые цилиндры, т.е. поле 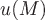 в цилиндрической системе координат задается функцией, зависящей ишь от одной координаты в цилиндрической системе координат задается функцией, зависящей ишь от одной координаты 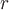 , то поле называется цилиндрическим. , то поле называется цилиндрическим.
Сферическое поле
Если значения поля 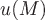 зависят лишь от расстояния точки зависят лишь от расстояния точки  до некоторой фиксированной точки до некоторой фиксированной точки 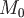 , то такое поле называется сферическим полем. , то такое поле называется сферическим полем.
Поверхности уровня такого поля - семейство концентрических сфер.
Вопрос. Скалярное поле потенциала электрического заряда 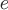 , задаваемого формулой , задаваемого формулой 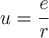 , где , где 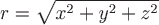 , является , является
Плоскопараллельным
Сферическим
Цилиндрическим
Осесимметрическим
Векторное поле
Определение. Если в каждой точке  пространственной области пространственной области  задан определенный вектор задан определенный вектор 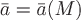 , то говорят, что в этой области задано векторное поле. , то говорят, что в этой области задано векторное поле.
Если в пространстве выбрать декартову систему координат, то векторное поле задается тремя скалярными полями (функциями) 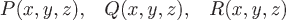 , являющимися проекциями вектора , являющимися проекциями вектора 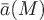 на координатные оси декартовой системы: на координатные оси декартовой системы:
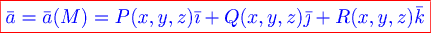 . .
Векторное поле тоже может быть плоским, например, 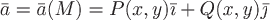 . .
В дальнейшем будем рассматривать векторные поля, компоненты которых непрерывны и имеют непрерывные частные производные первого порядка.
Примерами векторных полей могут служить:
1) поле скоростей стационарного потока жидкости (оно определяется так: пусть область  заполнена жидкостью, текущей текущей в каждой точке с некоторой скорость заполнена жидкостью, текущей текущей в каждой точке с некоторой скорость 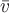 , не зависящей от времени, но различной в разных точках области; тогда поставив в соответствие каждой точке , не зависящей от времени, но различной в разных точках области; тогда поставив в соответствие каждой точке 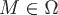 вектор вектор 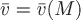 , получим векторное поле скоростей жидкости); , получим векторное поле скоростей жидкости);
2) поле тяготения (пусть в пространстве распределена некоторая масса, тогда на материальную точку  единичной массы действует гравитационная сила); единичной массы действует гравитационная сила);
3) электрическое поле (если в пространстве распределены каким-либо образом заряды, то на единичный электрический заряд , помещенный в точку  , эти заряды действуют с определенной силой , эти заряды действуют с определенной силой 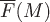 . .
Определение. Векторной линией поля  называется такая линия, в каждой точке которой касательная направлена вдоль заданного в этой точке вектора поля. называется такая линия, в каждой точке которой касательная направлена вдоль заданного в этой точке вектора поля.
Если векторное поле 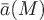 есть поле скоростей жидкости, то векторные линии - это траектории частиц жидкости. есть поле скоростей жидкости, то векторные линии - это траектории частиц жидкости.
Напряженность электростатического поля определяется вектором 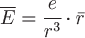 , где , где 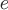 - электрический заряд, - электрический заряд, 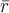 - радиус-вектор направления, соединяющего заряд с точкой поля. Поэтому для положительного заряда векторными линиями будут лучи, выходящие из заряда. - радиус-вектор направления, соединяющего заряд с точкой поля. Поэтому для положительного заряда векторными линиями будут лучи, выходящие из заряда.
Для магнитного поля векторными линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
Найдем уравнения векторных линий. Пусть 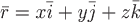 есть радиус-вектор какой-нибудь векторной линии. Тогда вектор есть радиус-вектор какой-нибудь векторной линии. Тогда вектор 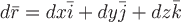 направлен по касательной к ней. По определению векторного поля векторы направлен по касательной к ней. По определению векторного поля векторы  и и 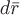 должны быть коллинеарны, откуда следует пропорциональность их проекций. Поэтому всякое векторное поле должны быть коллинеарны, откуда следует пропорциональность их проекций. Поэтому всякое векторное поле 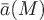 обладает семейством векторных линий. Уравнения этого семейства есть общее решение дифференциальных уравнений вида обладает семейством векторных линий. Уравнения этого семейства есть общее решение дифференциальных уравнений вида
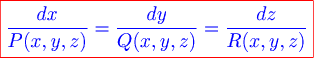
Замечание. Если векторное поле плоское, то дифференциальное уравнение векторных линий имеет вид:
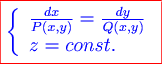
В силу теоремы существования и единственности через каждую точку  , при соблюдении условий этой теоремы, будет проходить одна определенная векторная линия. Если провести все векторные линии, проходящие через все точки некоторого куска поверхности , при соблюдении условий этой теоремы, будет проходить одна определенная векторная линия. Если провести все векторные линии, проходящие через все точки некоторого куска поверхности 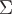 , то их совокупность даст векторную трубку. Причем нормаль , то их совокупность даст векторную трубку. Причем нормаль 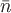 к векторной трубке в некоторой точке ортогональна вектору к векторной трубке в некоторой точке ортогональна вектору 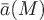 , т.е. , т.е. 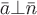 . .
Пример 1. Для плоского векторного поля 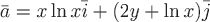 найти уравнения семейства векторных линий и векторной линии, проходящей через точку найти уравнения семейства векторных линий и векторной линии, проходящей через точку 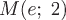 . .
Решение.
Так как 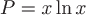 и и 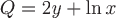 , то, согласно замечанию, уравнение семейства определяется общим решением дифференциального уравнения , то, согласно замечанию, уравнение семейства определяется общим решением дифференциального уравнения
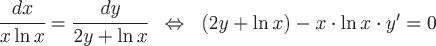 . .
Это уравнение линейное первого порядка. Решая его методом вариации произвольной постоянной, получим общее решение в виде 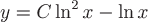 . .
Выделим из этого семейства одно решение – то, которое представляет собой уравнение векторной линии, проходящей через точку 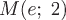 . Подставив в общее решение . Подставив в общее решение  и и 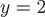 , получим , получим  . Итак, искомая векторная линия . Итак, искомая векторная линия 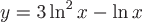 (синим цветом на чертеже отмечена точка с координатами (синим цветом на чертеже отмечена точка с координатами 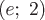 ). ). |
|
|
 Скачать 0.77 Mb.
Скачать 0.77 Mb.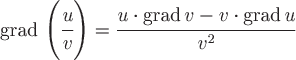 .
.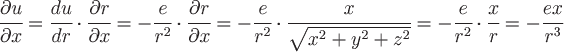 .
.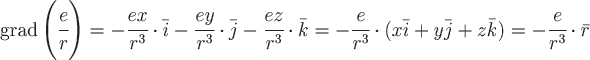 , где
, где