|
|
Определение. Числовая функция, заданная в каждой точке некоторой пространственной области, называется скалярным полем
                                                       Скалярное поле Скалярное поле
Термин "поле" обычно употребляется в физике для обозначения части пространства (или всего пространства), в которой рассматривается некоторое физическое явление. Если речь идет о процессе, характеризующемся скалярной величиной (температура, давление и т.д.), поле называется скалярным.
Определение. Числовая функция 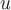 , заданная в каждой точке , заданная в каждой точке  некоторой пространственной области некоторой пространственной области  , называется скалярным полем (то есть каждой точке , называется скалярным полем (то есть каждой точке  этой области ставится в соответствие число этой области ставится в соответствие число 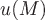 ). ).
Введя в области, где задано скалярное поле, декартовы координаты, можно представить это поле в виде функции 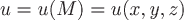 , определенной в области , определенной в области  . Если поле задано функцией двух переменных . Если поле задано функцией двух переменных 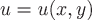 , то оно называется плоским. Эту функцию мы всегда в дальнейшем будем предполагать непрерывной и имеющей непрерывные частные производные первого порядка по всем переменным. , то оно называется плоским. Эту функцию мы всегда в дальнейшем будем предполагать непрерывной и имеющей непрерывные частные производные первого порядка по всем переменным.
Можно добавить, что величина 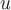 , характеризующая скалярное поле, может зависеть не только от координат точки , характеризующая скалярное поле, может зависеть не только от координат точки  , но также и от времени. Однако мы ограничимся рассмотрением лишь таких полей, где , но также и от времени. Однако мы ограничимся рассмотрением лишь таких полей, где 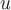 не зависит от времени. Такие поля называются стационарными. не зависит от времени. Такие поля называются стационарными.
Примерами скалярных полей могут служить:
1) поле температур некоторого нагретого тела (в каждой точке  этого тела этого тела  задана соответствующая температура задана соответствующая температура 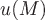 ), ),
2) потенциал электростатического поля задается формулой
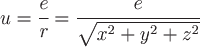 , ,
где 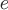 - заряд, а - заряд, а 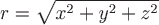 - расстояние от произвольной точки - расстояние от произвольной точки  до заряда, помещенного в начало координат, до заряда, помещенного в начало координат,
3) поле давлений,
4) поле плотности вещества и др.
Геометрической характеристикой скалярного поля служат поверхности уровня – множества точек пространства, в которых функция принимает постоянное значение: 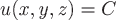 – уравнение различных поверхностей уровня при различных значениях – уравнение различных поверхностей уровня при различных значениях 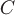 . .
В плоском поле 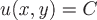 – уравнение линий уровня. С помощью линий уровня обычно изображаются рельеф местности на топографических картах, а именно, на них проводятся линии, состоящие из точек, имеющих одну и ту же высоту над уровнем моря (эти линии называются горизонталями). Распределение температур, давления, количества осадков и т.п. обычно также изображаются на специальных картах с помощью соответствующих линий уровня (они называются изотермами в случае поля температур или изобарами в случае поля давления). – уравнение линий уровня. С помощью линий уровня обычно изображаются рельеф местности на топографических картах, а именно, на них проводятся линии, состоящие из точек, имеющих одну и ту же высоту над уровнем моря (эти линии называются горизонталями). Распределение температур, давления, количества осадков и т.п. обычно также изображаются на специальных картах с помощью соответствующих линий уровня (они называются изотермами в случае поля температур или изобарами в случае поля давления).
Пример 1. Построить поверхности уровня потенциала электростатического поля 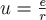 . .
Решение.
Так как 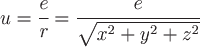 , то поверхности уровня будут задаваться так: , то поверхности уровня будут задаваться так:
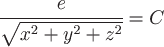 или или 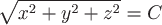 , ,
где 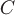 - некоторое положительное число, при этом для электростатического поля заряд - некоторое положительное число, при этом для электростатического поля заряд 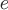 есть величина постоянная. есть величина постоянная.
Возведем в квадрат обе части последнего равенства и получим уравнение сферы с центром в начале координат 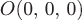 и переменным радиусом и переменным радиусом  : :
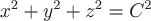 . .
Значит, поверхностями уровня электростатического поля будет семейство концентрических сфер с центром в точке, где находится заряд 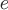 . .
При изучении скалярного поля методами анализа мы должны в первую очередь описать его локальные свойства, т.е. изменение величины 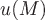 при переходе от данной точки при переходе от данной точки  к близким точкам. Для этого используют понятие производной по направлению. к близким точкам. Для этого используют понятие производной по направлению.
Пусть скалярное поле 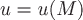 определено в области определено в области 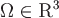 . .
Зафиксируем точку 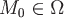 и выберем некоторое направление, определяемое вектором и выберем некоторое направление, определяемое вектором 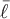 ; если существует предел ; если существует предел 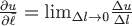 , то его называют производной функции , то его называют производной функции 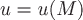 по направлению по направлению 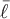 в заданной точке в заданной точке 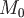 , где , где 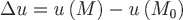 , , 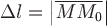 , , 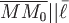 . .
Пусть скалярная функция 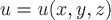 дифференцируема в точке дифференцируема в точке 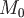 . Производную функции . Производную функции 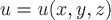 в точке в точке 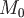 по направлению вектора по направлению вектора 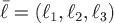 вычисляют по формуле вычисляют по формуле
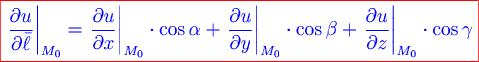 , ,
где 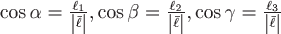 – направляющие косинусы вектора – направляющие косинусы вектора 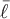 . .
Производная поля в данной точке 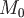 по направлению по направлению 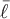 характеризует скорость изменения поля в этом направлении. характеризует скорость изменения поля в этом направлении.
Пример 2. Найти производную скалярного поля 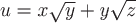 в точке в точке 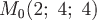 в направлении вектора в направлении вектора 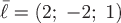 . .
Решение.
Для нахождения производной по направлению будем использовать формулу 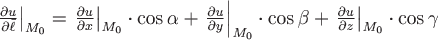
Найдем частные производные заданной функции:  . .
Вычислим значения частных производных в заданной точке 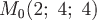 , т.е. при , т.е. при 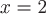 , , 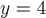 и и  : :
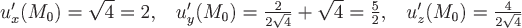 . .
Найдем значения направляющих косинусов:
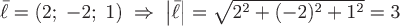 , ,
поэтому 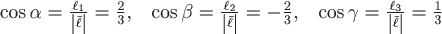 . .
Подставим все найденные величины в расчетную формулу для производной по направлению и получим:
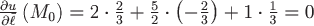 . .
Ответ: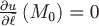 . .
Можно установить, что по направлению, касательному к поверхности уровня, производная от заданной функции равна нулю. Чтобы в этом убедиться, достаточно рассмотреть кривую, лежащую на поверхности уровня. Вдоль такой кривой приращение функции равно нулю 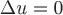 , т.к. на поверхности уровня значения функции постоянны. Поэтому , т.к. на поверхности уровня значения функции постоянны. Поэтому 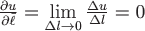 . .
Определение. Градиентом скалярного поля в точке  называется вектор называется вектор
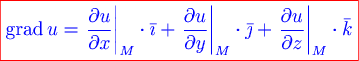
Между производной поля 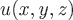 по направлению по направлению 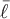 и градиентом в точке и градиентом в точке  существует следующая связь: существует следующая связь:
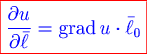 , ,
где 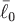 - орт вектора - орт вектора 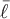 , т.е. единичный вектор, сонаправленный с вектором , т.е. единичный вектор, сонаправленный с вектором 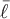 . .
Из этого равенства следует, что в каждой точке  , не являющейся критической, градиент направлен в сторону максимального возрастания поля , не являющейся критической, градиент направлен в сторону максимального возрастания поля 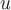 , а модуль градиента равен величине скорости этого возрастания: , а модуль градиента равен величине скорости этого возрастания:
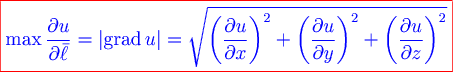 . .
|
|
|
 Скачать 0.77 Mb.
Скачать 0.77 Mb.





















































 Скалярное поле
Скалярное поле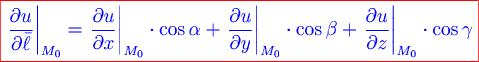 ,
,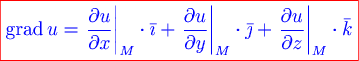
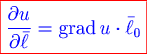 ,
,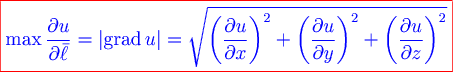 .
.