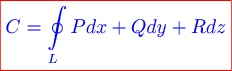|
|
Определение. Числовая функция, заданная в каждой точке некоторой пространственной области, называется скалярным полем
Теорема. Поток вектора 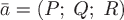 через внешнюю сторону замкнутой поверхности через внешнюю сторону замкнутой поверхности  равен тройному интегралу от дивергенции равен тройному интегралу от дивергенции 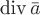 по области по области 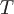 , ограниченной поверхностью , ограниченной поверхностью  . .
Следствие 1. Если для векторного поля  дивергенция равна нуль, т.е. дивергенция равна нуль, т.е. 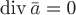 , то поток вектора , то поток вектора  через любую замкнутую поверхность равен нулю. через любую замкнутую поверхность равен нулю.
Следствие 2. Пусть в точке  имеется изолированный источник или сток, т.е. имеется изолированный источник или сток, т.е. 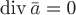 всюду в поле, кроме самой точки всюду в поле, кроме самой точки  . Тогда поток вектора . Тогда поток вектора  через замкнутую поверхность через замкнутую поверхность  , содержащую внутри себя точку , содержащую внутри себя точку  , не зависит от формы поверхности. , не зависит от формы поверхности.
Пример 1. Вычислить поток через любую замкнутую поверхность поля напряженности 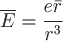 электростатического поля, образованного зарядом электростатического поля, образованного зарядом 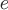 , помещенным в начало координат (здесь , помещенным в начало координат (здесь 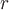 - расстояние от точки поля до заряда, - расстояние от точки поля до заряда, 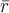 - радиус-вектор точки поля). - радиус-вектор точки поля).
Решение.
Ранее было установлено, что 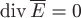 всюду, кроме начала координат, где помещен заряд всюду, кроме начала координат, где помещен заряд 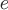 . .
Если замкнутая поверхность  не содержит внутри себя заряда не содержит внутри себя заряда 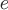 , то внутри нее , то внутри нее 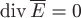 . Тогда по следствию 1 из теоремы Остроградского-Гаусса поток вектора . Тогда по следствию 1 из теоремы Остроградского-Гаусса поток вектора 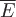 через через  равен нулю. равен нулю.
Если поверхность  содержит внутри себя заряд содержит внутри себя заряд 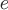 , то по следствию 2 получим, что поток вектора , то по следствию 2 получим, что поток вектора 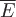 не зависит от вида поверхности. Поэтому в качестве замкнутой поверхности не зависит от вида поверхности. Поэтому в качестве замкнутой поверхности  возьмем сферу радиуса возьмем сферу радиуса 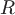 с центром в начале координат. с центром в начале координат.
Внешняя нормаль к сфере направлена по вектору 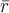 и имеет одинаковое направление с и имеет одинаковое направление с 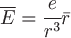 . В этом случае . В этом случае 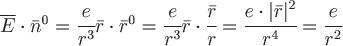 . .
На сфере длина радиус-вектора сохраняет постоянное значение, равное радиусу сферы, т.е.  или или 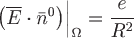 . .
Поэтому поток вектора напряженности 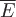 через поверхность шара радиуса через поверхность шара радиуса 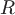 будет равен: будет равен:
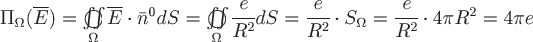 , ,
где 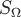 - площадь поверхности шара радиуса - площадь поверхности шара радиуса 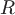 . .
Пример 2. Вычислить поток векторного поля 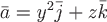 через замкнутую поверхность через замкнутую поверхность  , ограниченную , ограниченную 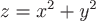 и и  , в направлении внешней нормали. , в направлении внешней нормали.
Решение.
Поле 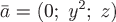 дифференцируемо во всем пространстве, поэтому получим дифференцируемо во всем пространстве, поэтому получим
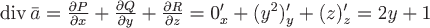 , ,
тогда по теореме Остроградского-Гаусса поток будет равен
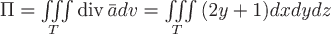 , ,
где 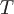 – область, в которой задано векторное поле – область, в которой задано векторное поле  и ограниченное замкнутой поверхностью и ограниченное замкнутой поверхностью  . .
Интеграл удобно вычислять в цилиндрических координатах:  . .
Причем область 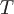 перейдет в область перейдет в область 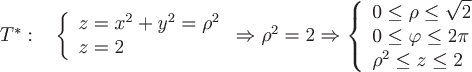
Вернемся к вычислению потока вектора  : :
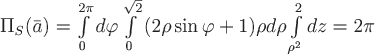 . .
Ответ:  . .
Вопрос. Поток векторного поля 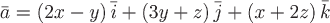 через замкнутую поверхность через замкнутую поверхность  может быть вычислен по формуле: может быть вычислен по формуле:
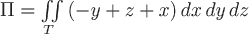
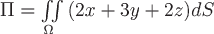
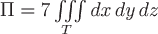
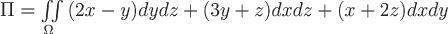
Циркуляция векторного поля
Пусть в области  задано непрерывное векторное поле задано непрерывное векторное поле 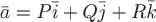 и ориентированная гладкая кривая и ориентированная гладкая кривая 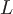 (с заданным направлением обхода). Обозначим единичный вектор касательной к линии (с заданным направлением обхода). Обозначим единичный вектор касательной к линии 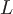 через через 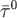 , направление которого совпадает с выбранным направлением на линии. , направление которого совпадает с выбранным направлением на линии.
Определение. Линейным интегралом векторного поля  вдоль линии вдоль линии 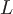 называется криволинейный интеграл 1 рода от скалярного произведения векторов называется криволинейный интеграл 1 рода от скалярного произведения векторов  и и 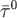 : :
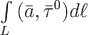 , ,
где 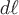 – дифференциал длины дуги кривой. – дифференциал длины дуги кривой.
Если ввести в рассмотрение вектор 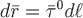 (здесь (здесь 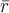 – радиус вектор точки, описывающий линию – радиус вектор точки, описывающий линию 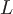 ) и обозначить его проекции на координатные оси через ) и обозначить его проекции на координатные оси через 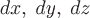 , то предыдущую формулу можно записать в виде , то предыдущую формулу можно записать в виде
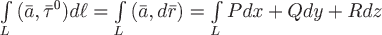 , ,
где вектор 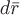 направлен по касательной к направлен по касательной к 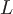 . Правая часть последнего равенства является криволинейным интегралом 2 рода. . Правая часть последнего равенства является криволинейным интегралом 2 рода.
Если  – силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной линии – силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной линии 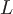 . .
Определение. Линейный интеграл называется циркуляцией векторного поля  , если , если 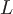 – замкнутая линия. – замкнутая линия.
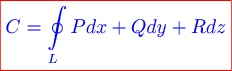
Если 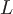 – замкнутая пространственная кривая, то ее направление обхода специально оговаривается. – замкнутая пространственная кривая, то ее направление обхода специально оговаривается.
Пример. Вычислить циркуляцию векторного поля 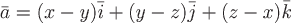 по замкнутой линии по замкнутой линии 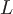 , состоящей из одного витка винтовой линии , состоящей из одного витка винтовой линии 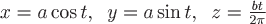 от точки от точки 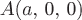 до точки до точки 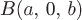 и прямолинейного отрезка и прямолинейного отрезка 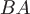 . .
Решение.
Виток 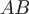 соответствует изменению параметра соответствует изменению параметра  в уравнениях кривой от в уравнениях кривой от 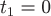 до до 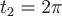 . Прямая . Прямая 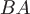 имеет направляющий вектор имеет направляющий вектор 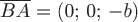 , поэтому ее параметрические уравнения будут , поэтому ее параметрические уравнения будут 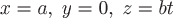 , где , где  изменяется от изменяется от 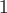 до до 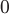 . Вычислим циркуляцию как сумму криволинейных интегралов по дуге винтовой линии и по прямолинейному отрезку: . Вычислим циркуляцию как сумму криволинейных интегралов по дуге винтовой линии и по прямолинейному отрезку:

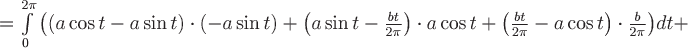
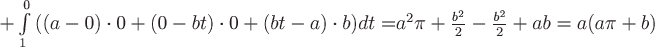 . .
Ответ: 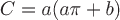 . .
Вопрос. Циркуляция векторного поля 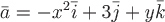 по замкнутому контуру по замкнутому контуру 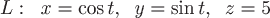 , где , где 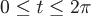 , может быть вычислена по формуле: , может быть вычислена по формуле:
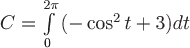
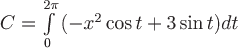
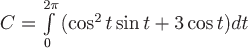
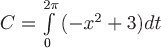 |
|
|
 Скачать 0.77 Mb.
Скачать 0.77 Mb.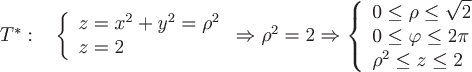
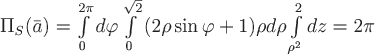 .
.