|
|
Определение. Числовая функция, заданная в каждой точке некоторой пространственной области, называется скалярным полем
Вопрос. Поток векторного поля 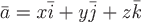 через часть плоскости через часть плоскости 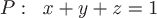 , лежащей в первом октанте, т.е. при , лежащей в первом октанте, т.е. при 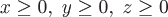 , (нормаль , (нормаль 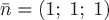 составляет острый угол с осью составляет острый угол с осью 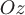 ) )
выражается формулой
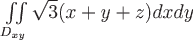
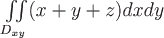
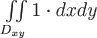
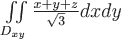
Дивергенция
Рассмотрим векторное поле  и некоторую замкнутую поверхность и некоторую замкнутую поверхность  в этом поле. Допустим, что поток вектора в этом поле. Допустим, что поток вектора  через внешнюю сторону поверхности через внешнюю сторону поверхности  положителен, т.е. положителен, т.е. 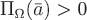 . .
Если рассматривать заданное векторное поле как поле скоростей движущейся жидкости, то положительность потока указывает, что количество жидкости, вытекающей из тела 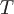 , заключенного внутри замкнутой поверхности , заключенного внутри замкнутой поверхности  , больше, чем количество жидкости, втекающей в это тело. То есть внутри тела , больше, чем количество жидкости, втекающей в это тело. То есть внутри тела 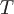 должны находиться источники поля, обильность (или интенсивность) которых характеризуется величиной потока через должны находиться источники поля, обильность (или интенсивность) которых характеризуется величиной потока через  . Аналогично в случае отрицательного потока внутри тела должны находиться стоки. Характеристикой интенсивности источника или стока служит средняя удельная интенсивность, которая определяется отношением потока . Аналогично в случае отрицательного потока внутри тела должны находиться стоки. Характеристикой интенсивности источника или стока служит средняя удельная интенсивность, которая определяется отношением потока 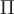 вектора вектора  через замкнутую поверхность через замкнутую поверхность  к объему к объему 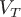 тела тела 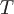 , ограниченного поверхностью: , ограниченного поверхностью: 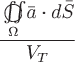 . .
Чтобы получить характеристику удельной интенсивности источника (или стока) в каждой отдельной точке, поступают так. Рассмотрим некоторую точку  векторного поля векторного поля  и заключим ее внутри небольшой замкнутой поверхности и заключим ее внутри небольшой замкнутой поверхности  (например, внутри сферы достаточно малого радиуса). Объем тела, ограниченного поверхностью (например, внутри сферы достаточно малого радиуса). Объем тела, ограниченного поверхностью  обозначим обозначим 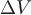 . Разделив поток . Разделив поток 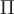 вектора вектора  через замкнутую поверхность через замкнутую поверхность  на объем на объем 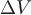 , получим среднюю удельную интенсивность , получим среднюю удельную интенсивность 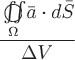 . Предел этой величины, когда объем . Предел этой величины, когда объем 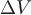 стремится к нулю и стремится к нулю и 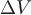 стягивается в точку стягивается в точку  , если такой предел существует, называют дивергенцией вектора , если такой предел существует, называют дивергенцией вектора  и обозначают и обозначают 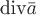 . .
Определение. Дивергенцией векторного поля  в точке в точке  называется предел отношения потока поля через замкнутую поверхность называется предел отношения потока поля через замкнутую поверхность  , окружающую точку , окружающую точку  , к объему , к объему 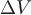 тела тела 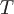 , ограниченного этой поверхностью, при стремлении диаметра , ограниченного этой поверхностью, при стремлении диаметра 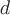 тела тела 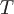 к нулю: к нулю:
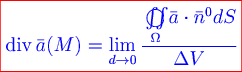
По знаку дивергенции можно судить о наличии источника или стока векторного поля в точке  . Так, если . Так, если 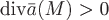 , то в точке , то в точке  – источник, а если – источник, а если 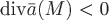 , то – сток. Если , то – сток. Если 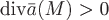 , то в точке , то в точке  нет ни источника, ни стока или они уравновешивают друг друга. Абсолютная величина нет ни источника, ни стока или они уравновешивают друг друга. Абсолютная величина 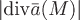 характеризует мощность источника или стока в точке характеризует мощность источника или стока в точке  . .
Можно доказать, что для векторного поля  в области в области 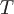 дивергенция равна дивергенция равна
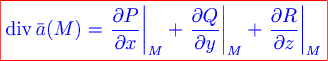
в любой точке 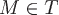 . .
На основании этой формулы можно проверить выполнимость свойств дивергенции.
1) 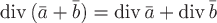 , ,
которое следует из линейности операции дифференцирования.
2) 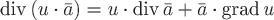 , ,
т.к. при 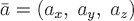 имеем имеем 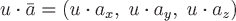 , поэтому , поэтому
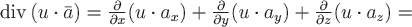
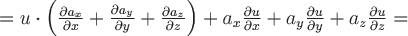
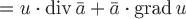 . .
3) 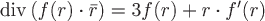 , ,
где 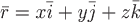 - радиус-вектор произвольной точки, - радиус-вектор произвольной точки, 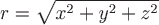 - расстояние от этой точки до начала координат. - расстояние от этой точки до начала координат.
Пример 1. Вычислить дивергенцию электростатического поля напряженности 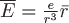 , создаваемого зарядом , создаваемого зарядом 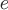 . .
Решение.
Воспользуемся свойством (3), в котором 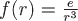 : :
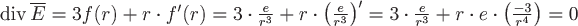 . .
Так как 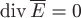 , то в любой точке поля, где определен вектор , то в любой точке поля, где определен вектор 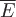 , нет ни источников ни стоков. , нет ни источников ни стоков.
Ответ: 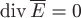 . .
Пример 2. Найти дивергенцию поля 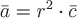 , где , где 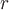 - расстояние от произвольной точки до начала координат, - расстояние от произвольной точки до начала координат, 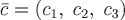 - постоянный вектор. - постоянный вектор.
Решение.
Т.к. 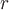 - расстояние от произвольной точки - расстояние от произвольной точки 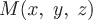 до начала координат до начала координат 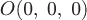 , то , то 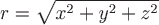 или или 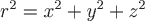 . .
Тогда вектор  имеет координаты имеет координаты 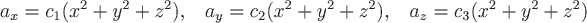 . .
По формуле 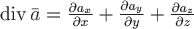 найдем дивергенцию заданного вектора: найдем дивергенцию заданного вектора:
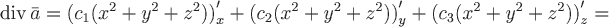
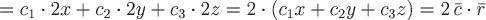 , ,
где 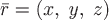 - радиус-вектор произвольной точки - радиус-вектор произвольной точки 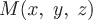 , т.е. , т.е. 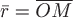 . .
Ответ: 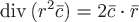 . .
Вопрос. Дивергенция векторного поля 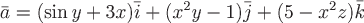 равна равна
(введите с клавиатуры только число)
Ваш ответ
3
Теорема Остроградского-Гаусса
Если функции 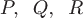 дифференцируемы в замкнутой области дифференцируемы в замкнутой области 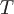 , ограниченной кусочно-гладкой поверхностью , ограниченной кусочно-гладкой поверхностью  , то имеет место формула Остроградского-Гаусса , то имеет место формула Остроградского-Гаусса
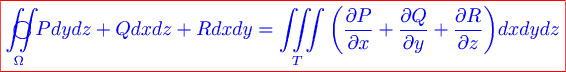 , ,
где выбрана внешняя сторона поверхности  . .
Для векторного поля  в области в области 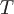 существует дивергенция, вычисляемая по формуле существует дивергенция, вычисляемая по формуле
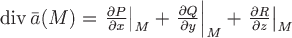
в любой точке 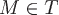 . .
Тогда формула Остроградского-Гаусса в векторной форме имеет вид
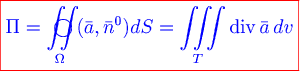 . .
|
|
|
 Скачать 0.77 Mb.
Скачать 0.77 Mb.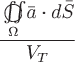 .
.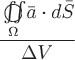 . Предел этой величины, когда объем
. Предел этой величины, когда объем 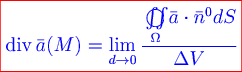
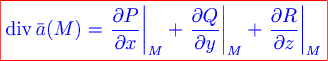
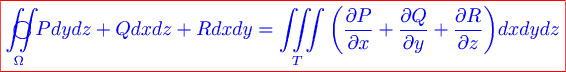 ,
,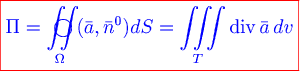 .
.