Математика. Определители. Свойства. Вычисление. Определитель или детерминант

Название	Определители. Свойства. Вычисление. Определитель или детерминант
Анкор	Математика.docx
Дата	24.02.2018
Размер	0.67 Mb.
Формат файла
Имя файла	Математика.docx
Тип	Документы #15865
страница	3 из 7

1 2 3 4 5 6 7

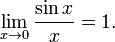
$\lim_{x \to 0}\frac{\sin x}{x} = 1.$

рвый замечательный предел

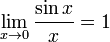
$\lim_{x \to 0}\frac{\sin x}{x} = 1$

Доказательство

sinx x limit proof.svg

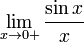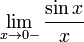Рассмотрим односторонние пределы $\lim_{x \to 0+}\frac{\sin x}{x}$ и $\lim_{x \to 0-}\frac{\sin x}{x}$ и докажем, что они равны 1.

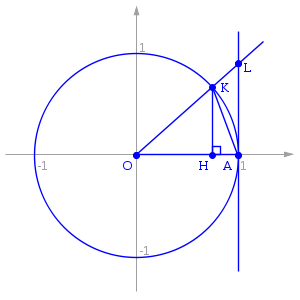
Пусть 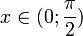$x \in (0; \frac{\pi}{2})$ . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

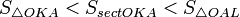$s_{\triangle oka} < s_{sect oka} < s_{\triangle oal}$ (1)

(где S_sectOKA — площадь сектора OKA)

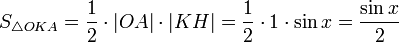
$s_{\triangle oka} = \frac{1}{2} \cdot |oa| \cdot |kh| = \frac{1}{2} \cdot 1 \cdot \sin x = \frac{\sin x}{2}$

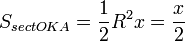
$s_{sect oka} = \frac{1}{2} r^2 x = \frac{x}{2}$

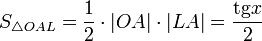
$s_{\triangle oal} = \frac{1}{2} \cdot |oa| \cdot |la| = \frac{\mathrm{tg} x}{2}$

(из : | LA | = tgx)

Подставляя в (1), получим:

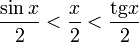
$\frac{\sin x}{2} < \frac{x}{2} < \frac{\mathrm{tg} x}{2}$

Так как при 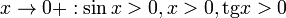$x \to 0+: \sin x> 0, x > 0, \mathrm{tg} x > 0$ :

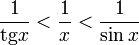
$\frac{1}{\mathrm{tg} x} < \frac{1}{x} < \frac{1}{\sin x}$

Умножаем на sinx:

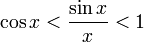
$\cos x < \frac{\sin x}{x} < 1$

Перейдём к пределу:

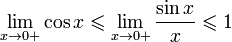
$\lim_{x \to 0+} \cos x \leqslant \lim_{x \to 0+}\frac{\sin x}{x} \leqslant 1$

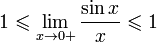
$1 \leqslant \lim_{x \to 0+}\frac{\sin x}{x} \leqslant 1$

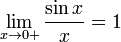
$\lim_{x \to 0+}\frac{\sin x}{x} = 1$

Найдём левый односторонний предел:

$\lim_{x \to 0-}\frac{\sin x}{x} = \left [ \begin{matrix} u = -x \\ x = -u \\ u \to 0+ \\ x \to 0- \end{matrix} \right ] = \lim_{u \to 0+}\frac{\sin(-u)}{-u} = \lim_{u \to 0+}\frac{-\sin(u)}{-u} = \lim_{u \to 0+}\frac{\sin(u)}{u} = 1$

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

$\lim_{x \to 0}\frac{\mathrm{tg} x}{x} = 1$
$\lim_{x \to 0}\frac{\arcsin x}{x} = 1$
$\lim_{x \to 0}\frac{\mathrm{arctg} x}{x} = 1$
$\lim_{x \to 0}\frac{1 - \cos x}{ \frac{x^2}{2} } = 1$

26. 2-ойзамечательный предел.
 Второй замечательный предел:

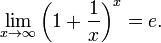
$\lim_{x \to \infty}\left(1 + \frac{1}{x}\right)^x = e.$

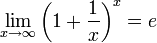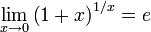
$\lim_{x \to \infty}\left(1 + \frac{1}{x}\right)^x = e$ или $\lim_{x \to 0}\left(1 + x\right)^{1/x} = e$

Доказательство второго замечательного предела:

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что $\lim_{x \to \infty}\left(1 + \frac{1}{x}\right)^x = e;x\mathcal{2}</h2>\mathbb r$ . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Отсюда следует: 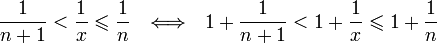$\frac{1}{n+1}<\frac{1}{x}\leqslant \frac{1}{n}</h2></h2>\longleftrightarrow</h2></h2>1+\frac{1}{n+1}<1+\frac{1}{x}\leqslant 1+\frac{1}{n}$ , поэтому

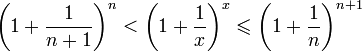$\left(1+\frac{1}{n+1}\right)^n<\left(1+\frac{1}{x}\right)^x\leqslant \left(1+\frac{1}{n}\right)^{n+1}$ .

Если , то . Поэтому, согласно пределу 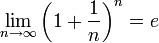$\lim_{n \to \infty}\left(1 + \frac{1}{n}\right)^n = e$ , имеем:

$\lim_{n \to \infty}\left(1 + \frac{1}{n+1}\right)^n = \frac{\lim\limits_{n \to \infty}(1 + \frac{1}{n+1})^{n+1}}{\lim\limits_{n \to \infty}\left(1 + \frac{1}{n+1}\right)} = \frac{e}{1}=e$

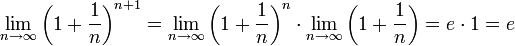$\lim_{n \to \infty}\left(1 + \frac{1}{n}\right)^{n+1} = \lim_{n \to \infty}\left(1 + \frac{1}{n}\right)^n\cdot \lim_{n \to \infty}\left(1 + \frac{1}{n}\right)=e\cdot 1=e$ .

По признаку (о пределе промежуточной функции) существования пределов 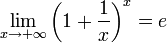$\lim_{x \to +\infty}\left(1 + \frac{1}{x}\right)^x = e$ .

2. Пусть . Сделаем подстановку − x = t, тогда

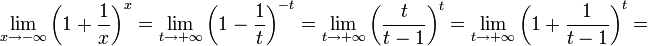
$\lim_{x \to -\infty}\left(1 + \frac{1}{x}\right)^x = \lim_{t \to +\infty}\left(1 - \frac{1}{t}\right)^{-t}= \lim_{t \to +\infty}\left(\frac{t}{t-1}\right)^t = \lim_{t \to +\infty}\left(1 + \frac{1}{t-1}\right)^t =$

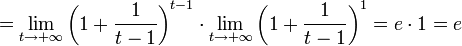$= \lim_{t \to +\infty}\left(1 + \frac{1}{t-1}\right)^{t-1}\cdot \lim_{t \to +\infty}\left(1 + \frac{1}{t-1}\right)^1 = e\cdot1=e$ .

Из двух этих случаев вытекает, что 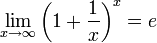$\lim_{x \to \infty}\left(1 + \frac{1}{x}\right)^x = e$ для вещественного x.

Следствия

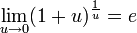
$\lim_{u \to 0}(1 + u)^\frac{1}{u}=e$
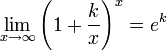
$\lim_{x \to \infty}\left(1 + \frac{k}{x}\right)^x = e^k$
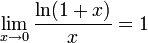
$\lim_{x \to 0}\frac{\ln(1 + x)}{x} = 1$
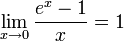
$\lim_{x \to 0}\frac{e^x - 1}{x} = 1$
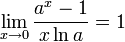$\lim_{x \to 0}\frac{a^x - 1}{x \ln a} = 1$ для 0 \,\!" ALIGN=BOTTOM WIDTH=46 HEIGHT=14 BORDER=0>,
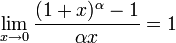
$\lim_{x \to 0}\frac{(1 + x)^\alpha - 1}{\alpha x} = 1$

27. Производная функции. Геометрический и физический смысл производной.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция 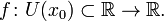$f\colon u(x_0) \subset \r \to \r.$ Производной функции f в точке x₀ называется предел, если он существует,

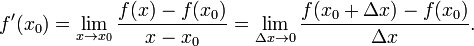
$f\'(x_0) = \lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0} = \lim_{\delta x \to 0} \frac{f(x_0+\delta x)-f(x_0)}{\delta x}.$

[править] Общепринятые обозначения производной функции y = f(x) в точке x₀

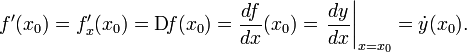
$f\'(x_0) = f\'_x(x_0)=\mathrm{d}\!f(x_0) = \frac{df}{dx}(x_0) = \left.\frac{dy}{dx}\right\vert_{x = x_0} = \dot{y}(x_0).$

Заметим, что последнее обычно обозначает производную по времени

Тангенс угла наклона касательной прямой

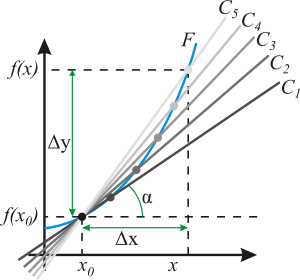
http://upload.wikimedia.org/wikipedia/commons/thumb/d/db/derivative-svg.svg/300px-derivative-svg.svg.png

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Основная статья: Касательная прямая

Если функция 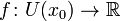$f\colon u(x_0) \to \r$ имеет конечную производную в точке x₀, то в окрестности U(x₀) её можно приблизить линейной функцией

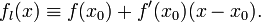
$f_l(x) \equiv f(x_0) + f\'(x_0)(x-x_0).$

Функция f_l называется касательной к f в точке x₀. Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

[править] Скорость изменения функции

Пусть s = s(t) — закон прямолинейного движения. Тогда v(t₀) = s'(t₀) выражает мгновенную скорость движения в момент времени t₀. Вторая производная a(t₀) = s''(t₀) выражает мгновенное ускорение в момент времени t₀.

Вообще производная функции y = f(x) в точке x₀ выражает скорость изменения функции в точке x₀, то есть скорость протекания процесса, описанного зависимостью y = f(x).

28. Правила дифференцирования функций. Таблица производных основных функций.

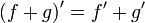
$\left({f + g}\right)\' = f\' + g\'$

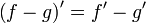
$\left({f - g}\right)\' = f\' - g\'$

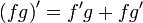$\left({fg}\right)\' = f\'g + fg\'$ (частный случай формулы Лейбница)

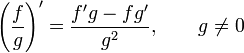
$\left({f \over g}\right)\' = {f\'g - fg\' \over g^2}, \qquad g \ne 0$

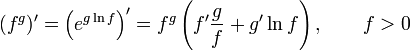
$(f^g)\' = \left(e^{g\ln f}\right)\' = f^g\left(f\'{g \over f} + g\'\ln f\right),\qquad f> 0$

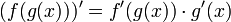$(f (g(x)))\' = f\'(g(x))\cdot g\'(x)$ — Правило дифференцирования сложной функции

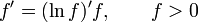
$f\' = (\ln f)\'f, \qquad f> 0$

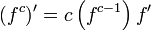
$(f^c)\' = c\left(f^{c-1}\right)f\'$