Математика. Определители. Свойства. Вычисление. Определитель или детерминант

Название	Определители. Свойства. Вычисление. Определитель или детерминант
Анкор	Математика.docx
Дата	24.02.2018
Размер	0.67 Mb.
Формат файла
Имя файла	Математика.docx
Тип	Документы #15865
страница	6 из 7

1 2 3 4 5 6 7

Производная параметрически заданной функции.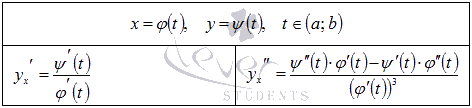

http://www.cleverstudents.ru/theory/images/parametrically_defined_function_derivative/030.png

В зависимости от правила, устанавливающего зависимость между множествами значений величин x и y, различают несколько способов задания функции. Наиболее привычным является представление функции в явном виде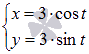

. Однако, в некоторых случаях удобно описывать функциональную зависимость множеством пар значений (x; y), которые вычисляются для каждого значения параметра t из промежутка (a; b). К примеру, все пары значений

при

задают окружность с центром в начале координат радиуса 3.

Определение параметрически заданной функции.

Таким образом, если

определены при

и существует обратная функция

для

, то говорят о параметрическом задании функции

.

При исследовании параметрически заданной функции иногда приходится находить ее производную по аргументу x. В этой статье мы выведем формулу производной параметрически заданной функции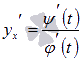

, также остановимся на производной второго и n-ого порядка.

Вывод формулы производной параметрически заданной функции.

Пусть

определены и дифференцируемы при

, причем

имеет обратную функцию

.

Сначала переходим от параметрического задания к явному. При этом получаем сложную функцию

, аргументом которой является x.
По правилу нахождения производной сложной функции имеем: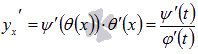

. Так как

обратные функции, то по формуле производной обратной функции

, поэтому

.

31. Производные высших порядков.

Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

Производные более высокого порядка (если они существуют), определяются как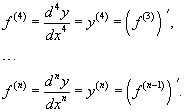

Для нахождения производных высшего порядка можно использовать следующие формулы: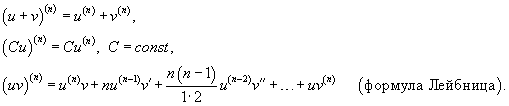

В частности, для производной второго и третьего порядка формула Лейбница принимает вид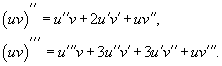

Пример 1

Найти y'', если

.

Решение.

Возьмем первую производную дифференцируя функцию как произведение.

Теперь найдем производную второго порядка

Пример 2

Вычислить y'' для параболы

.

Решение.

Дифференцируя как неявную функцию, имеем

Дифференцируя еще раз и используя правило для производной произведения, получаем

Умножим обе части на y² :

Поскольку yy' = 2, и следовательно, (yy' )² = 4, то последнее уравнение записывается в виде:



Отсюда следует, что



   Пример 3

Найти все производные функции

.

Решение.

Пусть u = e^x и v = x². Тогда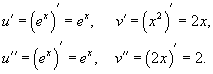

Легко устанавливаются общие формулы для производных n-порядка:

Используя формулу Лейбница

получаем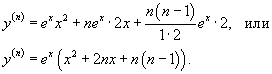

Пример 4

Определить все производные синуса.

Решение.

Вычислим несколько первых производных: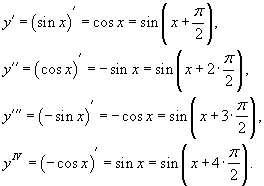

Очевидно, что производная n-го порядка выражается формулой

Пример 5

Найти все производные функции

.

Решение.

Аналогично предыдущему примеру, найдем сначала несколько первых производных.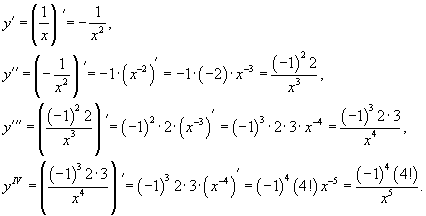

Этого достаточно, чтобы обнаружить общий "паттерн":

32. Дифференциал функции.

Дифференциал — линейная часть приращения функции.
Дифференциал функции в точке может быть определён как линейная функция

$d_{x_0}f(h) = f\'(x_0) h,$

где f'(x₀) обозначает производную f в точке x₀.

Таким образом df есть функция двух аргументов $df\colon (x_0,h)\mapsto d_{x_0}f(h)$ .

Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция $d_{x_0}f(h)$ линейно зависящая от h и для которой верно следующее соотношение

$d_{x_0}f(h)=f(x_0 + h) - f(x_0) + o(|h|).$

33. Правило Лопиталя.
Правило Бернулли^]-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
словия:

$\lim_{x\to a}{f(x)}=\lim_{x\to a}{g(x)}=0$ или ;
и дифференцируемы в проколотой окрестности ;
$g\'(x)\neq 0$ в проколотой окрестности ;
существует $\lim_{x\to a}{\frac{f\'(x)}{g\'(x)}}$ ,

тогда существует $\lim_{x\to a}{\frac{f(x)}{g(x)}} = \lim_{x\to a}{\frac{f\'(x)}{g\'(x)}}$ .

Пределы также могут быть односторонними.

1 2 3 4 5 6 7