Математика. Определители. Свойства. Вычисление. Определитель или детерминант

Название	Определители. Свойства. Вычисление. Определитель или детерминант
Анкор	Математика.docx
Дата	24.02.2018
Размер	0.67 Mb.
Формат файла
Имя файла	Математика.docx
Тип	Документы #15865
страница	7 из 7

1 2 3 4 5 6 7

Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида .

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку теорему Коши. По этой теореме получим:

$\exists c \in [a,x]\!:\frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f\'(c)}{g\'(c)}$ ,

но f(a) = g(a) = 0, поэтому $\forall x\, \exists c \in [a,\;x]\!:\frac{f(x)}{g(x)}=\frac{f\'(c)}{g\'(c)}$ .

Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим: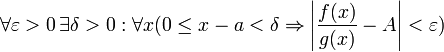

$\forall \varepsilon>0\, \exists \delta>0 : \forall x(0\le x-a<\delta\Rightarrow \left|\frac{f(x)}{g(x)}-A\right|<\varepsilon)$ для конечного предела и

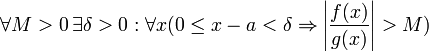$\forall m> 0\, \exists \delta>0 : \forall x(0\le x-a<\delta\Rightarrow \left|\frac{f(x)}{g(x)}\right| > M)$ для бесконечного,

что является определением предела отношения функций.

[править] Отношение бесконечно больших

Докажем теорему для неопределённостей вида $\left(\frac{\infty}{\infty}\right)$ .

Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:

$\forall\varepsilon_{1}>0\, \exists \delta_{1}>0 : \forall x(0\le x-a<\delta_{1}\Rightarrow \left| \alpha(x)\right| <\varepsilon_{1})$ .

Зафиксируем t из отрезка и применим теорему Коши ко всем x из отрезка :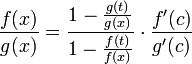

$\forall x\in [a;t]\ \exists c\in [a;\;x]\!:\frac{f(x)-f(t)}{g(x)-g(t)}=\frac{f\'(c)}{g\'(c)}$ , что можно привести к следующему виду:

$\frac{f(x)}{g(x)}=\frac{1-\frac{g(t)}{g(x)}}{1-\frac{f(t)}{f(x)}}\cdot\frac{f\'(c)}{g\'(c)}$ .

Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α:

$\forall \varepsilon_{1}>0\, \exists \delta_{2}>0\ : \forall x(0\le x-a<\delta_{2}\Rightarrow \left| \beta(x) \right| <\varepsilon_{1})$ .

Получили, что отношение функций представимо в виде (1 + β)(A + α), и 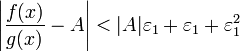$\left|\frac{f(x)}{g(x)}-a\right|<|a|\varepsilon_{1}+\varepsilon_{1}+\varepsilon_{1}^{2}$ . По любому данному ε можно найти такое ε₁, чтобы модуль разности отношения функций и A был меньше ε, значит, предел отношения функций действительно равен A.

Если же предел A бесконечен (допустим, он равен плюс бесконечности), то

$\forall m>0\, \exists \delta_{1}>0 : \forall x(0\le x-a<\delta_{1}\Rightarrow\frac{f'(x)}{g'(x)}>2M)$ .

В определении β будем брать ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда $\frac{f(x)}{g(x)}>\frac{1}{2}\cdot 2M=M\Rightarrow \lim_{x\to a+}{\frac{f(x)}{g(x)}}=+\infty$ .

Для других баз доказательства аналогичны приведённым

34. Исследование функции с помощью производной.

еорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f(x)  0.

                              2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

            Доказательство.

1)      Если функция f(x) возрастает, то f(x + x) > f(x) при x>0 и f(x + x) < f(x) при х<0,

тогда:

2) Пусть f(x)>0 для любых точек х₁ и х₂, принадлежащих отрезку [a, b], причем x₁2.



            Тогда по теореме Лагранжа: f(x₂) – f(x₁) = f()(x₂ – x₁),   x₁ <  < x₂

По условию f()>0, следовательно, f(x₂) – f(x₁) >0, т.е. функция f(x) возрастает.

Теорема доказана.

            Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f(x)0 на этом отрезке. Если f(x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b].

            Конечно, данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).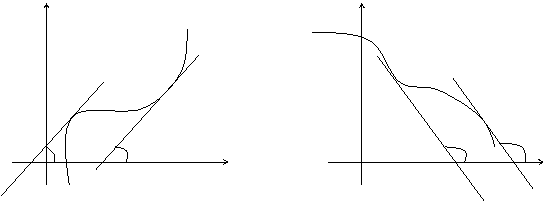

http://pipec8.narod.ru/mat/proizv/6.files/image002.gif

            Доказанную выше теорему можно проиллюстрировать геометрически:

               y                                                                            y

                                                                                                                                

                                                               x                                                                             x

Точки экстремума.

            Определение. Функция f(x) имеет в точке х₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х₁. Функция f(x) имеет в точке х₂ минимум, если f(x₂ +x) > f(x₂) при любом х (х может быть и отрицательным).

            Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.

            Определение. Точки максимума и минимума функции называются точками экстремума.

            Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х₁ и точка х₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

            Доказательство. Предположим, что функция f(x) имеет в точке х = х₁ максимум.

            Тогда при достаточно малых положительных х>0 верно неравенство:

, т.е.

            Тогда

            По определению:

Т.е. если х0, но х<0, то f(x₁)  0, а если х0, но х>0, то f(x₁)  0.

            А возможно это только в том случае, если при х0 f(x₁) = 0.

Для случая, если функция f(x) имеет в точке х₂ минимум теорема доказывается аналогично.

Теорема доказана.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х³, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.

Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.

Пример: f(x) = x                                              Пример: f(x) =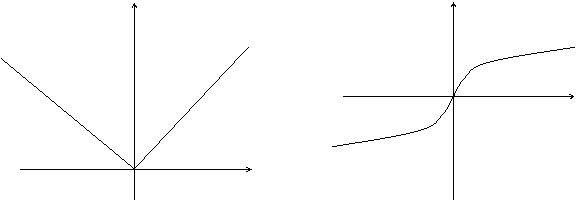

http://pipec8.narod.ru/mat/proizv/6.files/image009.gif

                              y                                                                             y

                                                                                                                                             x

                                                                 x



В точке х = 0 функция имеет минимум, но           В точке х = 0 функция не имеет ни

не имеет производной.                                            максимума, ни минимума, ни произ-

                                                                                  водной.

            Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.

            Теорема. (Достаточные условия существования экстремума)

            Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х₁, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х₁).

            Если при переходе через точку х₁ слева направо производная функции f(x) меняет знак с “+” на “-“, то в точке х = х₁ функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.

            Доказательство.

Пусть

По теореме Лагранжа:           f(x) – f(x₁) = f()(x – x₁),     где x <  < x₁.

            Тогда: 1) Если х < x₁, то  < x₁;      f()>0;    f()(x – x₁)<0, следовательно

f(x) – f(x₁)<0 или   f(x) < f(x₁).

                        2) Если х > x₁, то  > x₁   f()<0;    f()(x – x₁)<0, следовательно

f(x) – f(x₁)<0 или   f(x) < f(x₁).

Т. к. ответы совпадают, то можно сказать, что f(x) < f(x₁) в любых точках вблизи х₁, т.е. х₁ – точка максимума.

            Доказательство теоремы для точки минимума производится аналогично.

Теорема доказана.

На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:

1)      Найти критические точки функции.

2)      Найти значения функции в критических точках.

3)      Найти значения функции на концах отрезка.

4)      Выбрать среди полученных значений наибольшее и наименьшее.

35. Асимптоты графика функции.
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение: Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где 0$" ALIGN=BOTTOM WIDTH=42 HEIGHT=31 BORDER=0>

1 2 3 4 5 6 7