Математика. Определители. Свойства. Вычисление. Определитель или детерминант

Название	Определители. Свойства. Вычисление. Определитель или детерминант
Анкор	Математика.docx
Дата	24.02.2018
Размер	0.67 Mb.
Формат файла
Имя файла	Математика.docx
Тип	Документы #15865
страница	5 из 7

1 2 3 4 5 6 7

Производные гиперболических функций

${d \over dx}\,\operatorname{sh}\,x = \,\operatorname{ch}\,x$

${d \over dx}\,\operatorname{ch}\,x = \,\operatorname{sh}\,x$

${d \over dx}\,\operatorname{th}\,x = \,\operatorname{sech}^2\,x$

${d \over dx}\,\operatorname{sech}\,x = - \operatorname{th} x\,\operatorname{sech}\,x$

${d \over dx}\,\operatorname{cth}\,x = -\,\operatorname{csch}^2\,x$

${d \over dx}\,\operatorname{csch}\,x = -\,\operatorname{cth}\,x\,\operatorname{csch}\,x$

${d \over dx}\,\operatorname{arsh}\,x = { 1 \over \sqrt{x^2 + 1}}$

${d \over dx}\,\operatorname{arch}\,x = { 1 \over \sqrt{x^2 - 1}}$

${d \over dx}\,\operatorname{arth}\,x = { 1 \over 1 - x^2}$

${d \over dx}\,\operatorname{arsech}\,x = { 1 \over x\sqrt{1 - x^2}}$

${d \over dx}\,\operatorname{arcth}\,x = { 1 \over 1 - x^2}$

${d \over dx}\,\operatorname{arcsch}\,x = {-1 \over |x|\sqrt{1 + x^2}}$

29. Производная сложной функции.
Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру,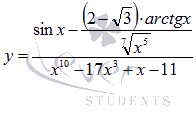

http://www.cleverstudents.ru/theory/images/combined_function_derivative/001.png

смотрится очень внушительно, но сложной эта функция не является, в отличие от

.

В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров.

При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами.

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а

- целая рациональная функция (смотрите классификацию элементарных функций), тогда

.

В свою очередь, g(x) также может быть сложной функцией. Например,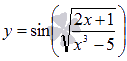

. Условно такое выражение можно обозначить как

. Здесь f – функция синуса, - функция извлечения квадратного корня,

- дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом

.

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции.

30. Производная функции, заданной в параметрической форме.

1 2 3 4 5 6 7