сысы. Организация и технология ремонта старогодной рельсошпальной решетки с железобетонными шпалами на производственной базе пмс216
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
 Мaкcимaльное значение cилы инерции, возникающее при качение колеса с непрерывной неровностью по пути  (2.14) (2.14)где k1 − коэффициент, характеризующий неравномерности образования проката поверхности катания колёс, принимаемый для электровозов равным0,23; α0 − коэффициент, учитывающий влияние колеблющейся массы пути; d − диаметр колеса, м. Среднеквадратическое отклонение расчетной нагрузки на рельс от сил инерции необреccоренной мaccы  , возникающих из-за наличия непрерывных неровностей на поверхности катания колёс вычисляется по формуле: , возникающих из-за наличия непрерывных неровностей на поверхности катания колёс вычисляется по формуле: (2.15) (2.15)где Рннкmax – максимальное значение силы инерции, Н. Подставив формулу (2.14) в формулу (2.15) получим: 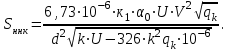 (2.16) (2.16)Максимальное значение силы инерции, передающейся на путь от колеса с изолированной неровностью, определяется по формуле: 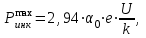 (2.17) (2.17)Среднеквадратическое отклонение динамической нагрузки колёс на рельс Sинк от сил инерции необрессоренной массы Ринк, возникающих из-за наличия на поверхности катания плавных изолированных неровностей, определяется по формуле:  (2.18) (2.18)где 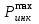 − максимальное значение силы инерции, Н. − максимальное значение силы инерции, Н.Подставив формулу (2.17) в формулу (2.18) получим  (2.19) (2.19)Согласно исходным данным найдем среднее квадратичное отклонение: 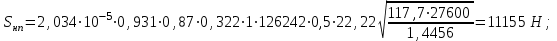 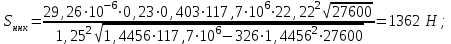    2.3. Эквивалентные нагрузки 2.3.1 Общие положения При движении поезда на путь воздействует система сосредоточенных сил давлений от колёс тележек. Самыми невыгодными (опасными) положениями такой подвижной нагрузки для расчётного сечения является расположение одного из колёс на вершине линии влияния. Учитывая то, что линии влияния изгибающих моментов и прогибов принятой модели пути быстро затухают, обычно бывает достаточно рассмотреть систему сил, состоящую из давлений трех последовательно расположенных колёс. Нагрузку, определяемую как сумму воздействий усилий от каждого из включенных в расчетную схему колёс в данном сечении, называют эквивалентной нагрузкой. При определении эквивалентных нагрузок считается, что одно из рассматриваемых колёс локомотива или вагона передает на рельс расчётную нагрузку, а другие – среднюю (т.е. вероятный максимум динамической нагрузки колеса, расположенного над расчетным сечением, не совпадает с вероятным максимумом нагрузок соседних колёс). 2.3.2 Эквивалентная нагрузка при определении изгибающего момента Максимальная эквивалентная нагрузка для расчётов напряжений в рельсах от изгиба определяется по формуле:  +∑µ(kхi) +∑µ(kхi) (2.20) (2.20)где µ( kxi ) -ординаты линии влияния изгибающих моментов рельса в сечениях пути, расположенных под колёсными нагрузками от осей, смежных с расчётной осью. µ(kхi)=  [сos(kхi)-sin(kхi)] (2.21) [сos(kхi)-sin(kхi)] (2.21)Для системы, состоящей из трех нагрузок, наиболее опасным расположением (установкой) колес относительно расчетного сечения является схема, показанная на рис. 2.2. 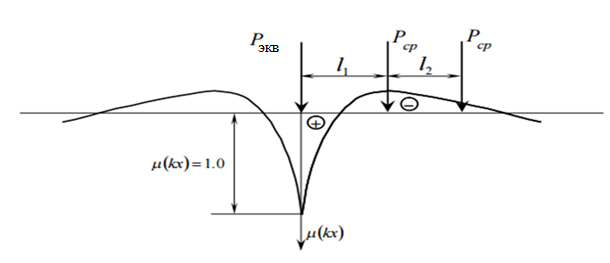 Рисунок 2.2–Схема определения эквивалентной нагрузки при расчёте изгибающего момента. Для этой установки координаты средних нагрузок равны х1=l1 х2=l1+ l2. Причем, для трехосной тележки l1 и l2 – это расстояния соответственно между первой и второй и второй и третьей осями тележки; а для двухосной l1 – это расстояние между осями тележки, а l2 – это расстояние между крайней осью первой тележки и первой осью следующей по ходу поезда тележки. Ординаты линий влияния изгибающих моментов рельса в сечениях пути, расположенных под колёсными нагрузками от осей тележки, смежных с расчётной осью будут составлять: µ1(1,4456·3)= е-1,4456·3·(cos(1,4456·3)–sin(1,4456·3))=0,007371; µ2 (1,4456·7,5)= е-1,4456·7,5·(cos (1,4456·7,5) – sin (1,4456·7,5))=0,000016; Тогда максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба будет равна: 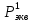 = 155282 + (0,007371·126242)+(0,000017·126242)=156214 Н. = 155282 + (0,007371·126242)+(0,000017·126242)=156214 Н.2.3.3 Эквивалентная нагрузка для определения прогиба рельса и давления на шпалу Эквивалентная нагрузка для определения прогиба рельса рассчитывается аналогичным образом. Максимальная эквивалентная нагрузка определяется по формуле, Н.  = = +∑ƞ(kхi)· +∑ƞ(kхi)·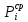 , (2.22) , (2.22)где ƞ(kxi) - ординаты линии влияния прогибов рельса в сечениях пути, расположенных под колёсными нагрузками от осей тележки, смежных с расчётной осью. Ƞ (kхi)=  (cos(kхi)+sin(kхi)) (2.23) (cos(kхi)+sin(kхi)) (2.23)При определении 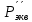 существуют две опасные установки колёсной нагрузки (рисунок 1.4). В большинстве случаев существуют две опасные установки колёсной нагрузки (рисунок 1.4). В большинстве случаев 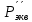 оказывается больше при расчете по схеме рис. 1.4 б. оказывается больше при расчете по схеме рис. 1.4 б. Рисунок 2.3 – Схема определения эквивалентной нагрузки при расчёте прогиба. Для этой установки координаты средних нагрузок равны x1 = 3, x2 = 4,5. Согласно исходным данным определим эквивалентную нагрузку  : :Ординаты линии влияния прогиба рельса и давления на шпалу в сечениях пути при расположение нагрузок по второй установке будут составлять µ1(1,4456·3)= е-1,4456·3·(cos(1,4456·3)+sin(1,4456·3))=-0,016960; µ2 (1,4719·4,5)= е-1,4456·4,5·(cos (1,4456·4,5) + sin (1,4456·4,5))=0,001788; Тогда максимальная эквивалентная нагрузка для определения прогиба рельса будет равна  = 155282 + (-0,016960·126242)+( 0,001788·126242)=153366 Н. = 155282 + (-0,016960·126242)+( 0,001788·126242)=153366 Н.2.4 Определение напряжений в элементах верхнего строения пути 2.4.1 Осевые напряжения в подошве рельса Осевые напряжения в подошве рельса от изгиба и вертикальной нагрузки определяется по формуле:  (2.24) (2.24)гдеW – момент сопротивления поперечного сечения рельса относительно нейтральной оси для удалённого волокна подошвы, м3; М – изгибающий момент в рельсе от воздействия эквивалентной нагрузки, Н  м. м.Изгибающий момент в рельсе от воздействия эквивалентной нагрузки определяется по формуле, Н·м:  (2.25) (2.25)Тогда согласно исходным данным найдем осевые напряжения в подошве рельса:   2.4.2 Кромочные напряжения в подошве рельса Вертикальная нагрузка от колеса на рельс имеет смещение (эксцентриситет) относительно оси симметрии сечения рельса. Со стороны гребня колеса на головку рельса действует горизонтальная сила. Вследствие этого в наиболее удалённых точках от центральных осей поперечного сечения рельса (наружная кромка подошвы и внутренняя кромка головки рельса) возникает сложное напряжённое состояние от совместного действия двух изгибающих моментов и крутящего момента.  Рисунок 2.4 – Схема приложения сил на рельс. Нормальные напряжения в кромке подошвы рельса вычисляются по формуле, Па:  (2.26) (2.26)где f – коэффициент перехода к кромочным напряжениям, зависящий от типа экипажа, радиуса кривой. Согласно исходным данным найдем кромочные напряжения в подошве рельса:  Па. Па.2.4.3 Напряжения в шпалах и в балластном слое под шпалой Напряжения смятия в деревянных шпалах под подкладками и в прокладках при железобетонных шпалах определяются по формуле: 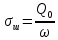 (2.27) (2.27)где  – площадь подкладки или подрельсовой прокладки, м2; – площадь подкладки или подрельсовой прокладки, м2;Q0 – нагрузка, передающая давление рельса на шпалу, Н. Напряжения в балластном слое под шпалой в подрельсовом сечении:  (2.28) (2.28)где 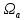 – эффективная опорная площадь полушпалы с учётом изгиба, м2. – эффективная опорная площадь полушпалы с учётом изгиба, м2.Нагрузка, передающая давление рельса на шпалу определяется по формуле  Согласно исходным данным найдем напряжение смятия в деревянных шпалах:   МПа; МПа;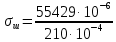 = 2,64 МПа. = 2,64 МПа.2.5 Напряжения на основной площадке земляного полотна Напряжения на основной площадке земляного полотна определяют в подрельсовом сечении под расчетной шпалой на глубине h с учетом давлений, передаваемых на балластный слой от соседних шпал. Напряжения определяются в точке М под расчетной шпалой как сумму воздействий от трех соседних шпал, на которую передается нагрузка от трех колес (рисунок 2.5). 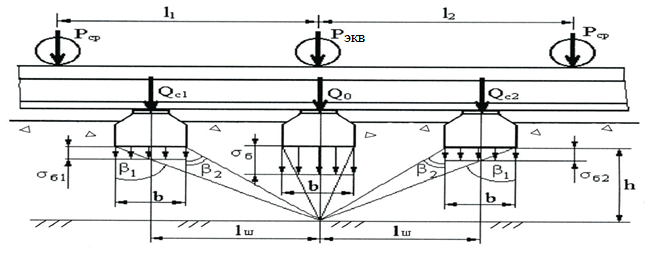 Рисунок 2.5 – Схема расчёта напряжений на основной площадке земляного полотна. В точке, находящейся на расстояние h от подошвы шпалы, напряжения определяются по формуле, Па:  , (2.29) , (2.29)где  - напряжения от воздействия расчётной шпалы на глубине h; - напряжения от воздействия расчётной шпалы на глубине h;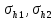 - напряжения от действия соседних шпал. - напряжения от действия соседних шпал.Предварительно определяют  , передающееся от рельса на расчетную шпалу и , передающееся от рельса на расчетную шпалу и  и и  на соседние шпалы. на соседние шпалы.Для этой цели расчетное колесо ставят под расчетной средней шпалой.  (2.30) (2.30)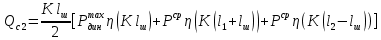 (2.31) (2.31)Зная величины давлений рельсов на шпалу находят напряжения в балласте под шпалами по следующим формулам:  (2.32) (2.32) (2.33) (2.33)Нормальные напряжения сжатия под расчетной шпалой определяется на основе решения плоской задачи теории упругости при рассмотрении шпального основания как однородной изотропной среды по формуле: 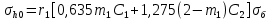 ; (2.34) ; (2.34) ; (2.35) ; (2.35) ; (2.36) ; (2.36)где r1 – поправочный коэффициент, учитывающий влияние материала шпал на напряжения, принимаемый для деревянных и железобетонных шпал 0,8 и 0,7 соответственно; m1 – коэффициент, учитывающий неравномерность напряжений по ширине подошвы шпалы, определяемый как:  (2.37) (2.37)и должен составлять не менее 1; С1, С2, Ah – константы, зависящие от геометрии шпального основания (ширины подошвы шпалы b, м, толщины балласта h, м, расстояния между осями шпал  , м), определяемые по формулам: , м), определяемые по формулам: (2.38) (2.38) (2.39) (2.39)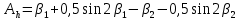 (2.40) (2.40)где 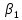 и и 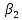 - углы лучей от края эпюры давления под шпалой к точке М - углы лучей от края эпюры давления под шпалой к точке М  и и . .Расчет:  . .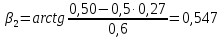 . . . . . . . .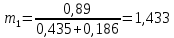 . . 0,6850836 0,6850836 -0,0362496 -0,0362496 -0,0038067 -0,0038067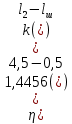 0,0012243 0,0012243 0,0010133 0,0010133 36840 Н. 36840 Н. 38330 Н. 38330 Н. 0,124МПа. 0,124МПа. МПа. МПа. 0,0363 МПа. 0,0363 МПа. 0,00890МПа. 0,00890МПа. 0,00925МПа. 0,00925МПа. МПа. МПа.Допускаемые напряжения Расчет рельсов и других элементов пути на прочность ведется по допускаемым напряжениям, которые ограничивают максимальные расчетные напряжения от поездной нагрузки. 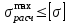 (2.42) (2.42)В соответствии с характером работы каждого из элементов пути регламентируются следующие виды допускаемых напряжений (оценочные критерии прочности пути), обеспечивающих прочность и надежность железнодорожного пути: [σк] – допускаемые напряжения растяжения в кромке подошвы рельса, обусловленные изгибом последнего и кручением от вертикального и горизонтального воздействия подвижного состава, МПа; [σш] – допускаемые напряжения на смятие в деревянных шпалах под прокладками и в прокладках для железобетонных шпал, МПа; [σб] – допускаемые напряжения сжатия в балласте под шпалой в подрельсовой зоне, МПа; [σh] – допускаемые напряжения сжатия на основной площадке земляного полотна, МПа. Превышение расчётных напряжений над допускаемыми указывает на необходимость усиления пути, причём превышение до 30% не является основанием для ограничения скорости движения поездов. Численные значения допускаемых напряжений в элементах верхнего строения пути (ВСП) зависят от вида подвижного состава и грузонапряжённости пути. В кривых радиусом 1000 м и менее рекомендуется принимать значение [σк] = 240 МПа независимо от грузонапряжённости. Также при железобетонных шпалах [σш] следует принимать 7,5 МПа для локомотивов. При песчанном балласте табличное значение [σб] следует уменьшить в 1,6 раза, а при гравии в 1,4. В таблице 2.1 представлено сравнение допускаемых и расчётных напряжений в элементах ВСП. Таблица 2.1 – Оценочные критерии прочности пути
Расчет пути на прочность на ПЭВМ Алгоритм расчёта пути на прочность, изложенный в разделах 2.1-2.7 реализован в инструментальной среде MathCAD, позволяющей выполнять многовариантные вычисления для различных конструкций пути и типов подвижного состава. Для удобства ввода информации в расчётный модуль заполним таблицу 2.2, содержащую исходные данные по выполнению расчёта от воздействия на путь локомотива ВЛ80. Таблица 2.2 – Исходные данные для расчёта пути на прочность в программной среде MathCAD
Результаты расчета пути на прочность на ПЭВМ сведены в таблицы 2.3 и 2.4. Таблица 2.3 – Результаты расчёта нагрузки
Таблица 2.4 – Результаты расчёта напряжений
На рисунках 2.6 – 2.10 представлены графики зависимости напряжений в элементах верхнего строения пути от скорости движения.  1-лето прямая; 2-лето кривая; 3-зима прямая; 4 зима кривая. Рисунок 2.6 – Зависимость осевых напряжений в подошве рельса от скорости движения (локомотива ВЛ80 ([  МПа)). МПа)). 1-лето прямая; 2-лето кривая; 3-зима прямая; 4 зима кривая. Рисунок 2.7 – Зависимость кромочных напряжений в подошве рельса от скорости движения (локомотива ВЛ80 ([  МПа)). МПа)). 1-лето прямая; 2-лето кривая; 3-зима прямая; 4 зима кривая. Рисунок 2.8 – Зависимость напряжений в подрельсовой прокладке от скорости движения (локомотива ВЛ80 ([  МПа)). МПа)). 1-лето прямая; 2-лето кривая; 3-зима прямая; 4 зима кривая. Рисунок 2.9 – Зависимость напряжений в балласте от скорости движения (локомотива ВЛ80 ([  МПа)). МПа)). 1-лето прямая; 2-лето кривая; 3-зима прямая; 4 зима кривая. Рисунок 2.10 – Зависимость напряжений на основной площадке земляного полотна от скорости движения (локомотива ВЛ80 ([  МПа)). МПа)).Из анализа рисунков 2.6 – 2.10 видно, что напряжения во всех элементах верхнего строения пути и на основной площадке земляного полотна не превышают допускаемые. Следовательно, рассматриваемая конструкция пути удовлетворяет условию прочности, и её можно использовать в заданных условиях эксплуатации без усиления и без снижения скоростей движения поездов. Вывод Анализ результатов расчета показал, что при повышении скорости движения грузового поезда с 20 до 80 км/ч напряжения в кромках подошвы рельсов под воздействием электровоза 80 в прямой и кривой R = 350 м возросли на 20 %. Наибольшие напряжения в нашпальных прокладках, в балласте и на основной площадке возникают в прямой зимой под воздействием электровоза ВЛ80 при скорости движения 80 км/ч и составляют: σш = 3,13 МПа, σб = 0,221 МПа и σh = 0,0595 МПа, что также меньше допускаемых значений [σш] = 7,5 МПа, [σб] = 0,4 МПа, [σh] = 0,1 МПа. Таким образом, при расчете железнодорожного пути на прочность от воздействия локомотив ВЛ80, было определено, что напряжения возникаемые в различных элементах верхнего строения пути не превышают допускаемые. Можно сделать вывод о безопасном использовании данного локомотива ВЛ80 на участках К дистанции пути. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 106
106