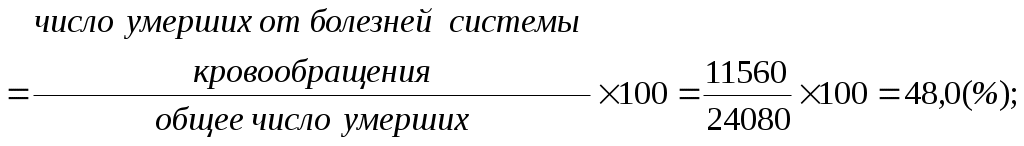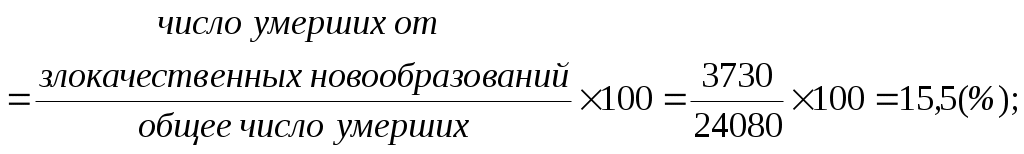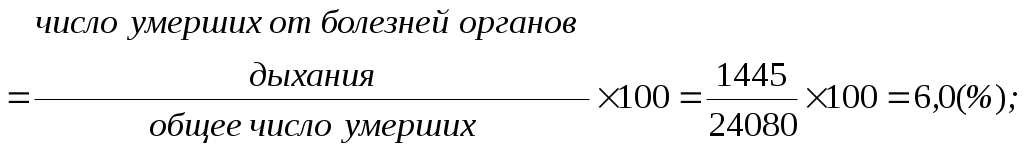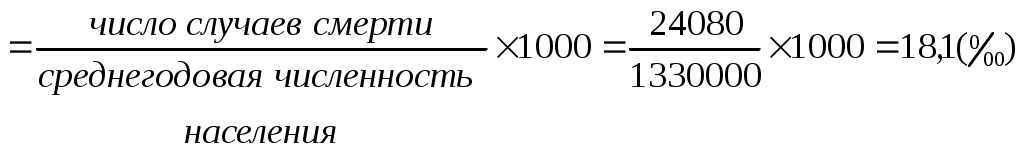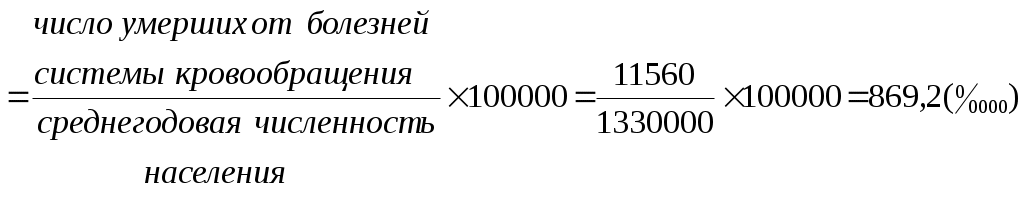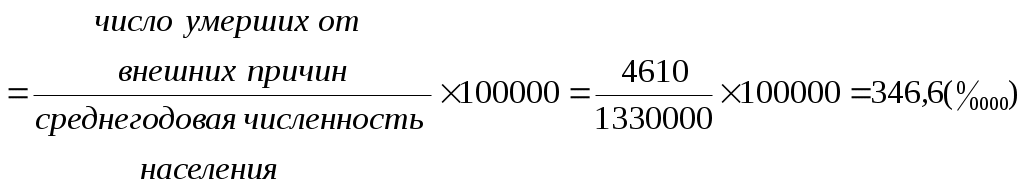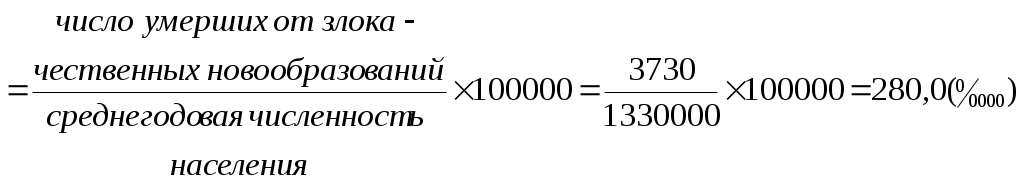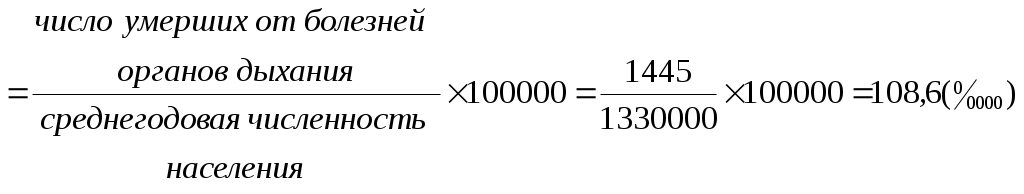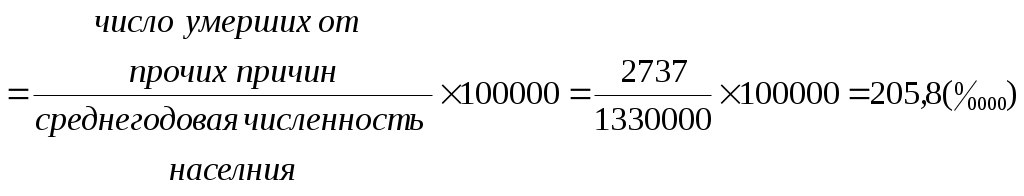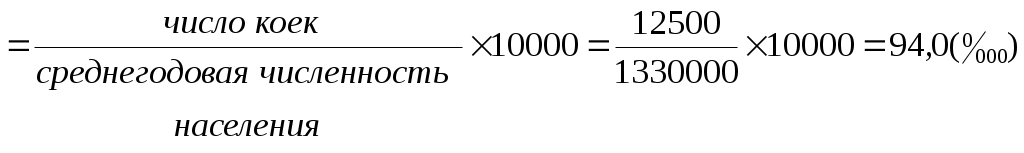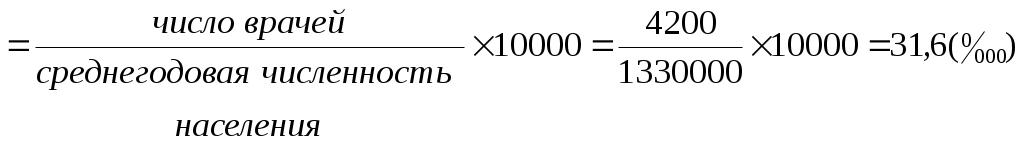Организация медикосоциальных исследований и методы статистического анализа Модуль Абсолютные и относительные статистические показатели Цель изучения модуля

• Название: Организация медикосоциальных исследований и методы статистического анализа Модуль Абсолютные и относительные статистические показатели Цель изучения модуля
• Дата: 25.04.2023
• Размер: 0.83 Mb.
• Имя файла: Chast_1_stom.doc
• Тип: Документы; #1088579
• страница: 1 из 5

Часть 1. Организация медико-социальных исследований и методы статистического анализа
Модуль 2. Абсолютные и относительные статистические показатели
Цель изучения модуля: показать значение абсолютных и относительных статистических показателей для изучения общественного здоровья, деятельности системы (организаций) здравоохранения и в клинической практике.

После изучения темы студент должен знать:

• 
  виды относительных статистических показателей;
  
• 
  методику расчета, анализа и графического изображения относительных статистических показателей.
  

Студент должен уметь:

• 
  выбирать тот или иной вид относительных статистических показателей в конкретной ситуации для анализа общественного здоровья, деятельности системы (организаций) здравоохранения и в клинической практике;
  
• 
  рассчитывать, анализировать и представлять графически относительные статистические показатели;
  
• 
  использовать полученные знания при обучении на клинических кафедрах.
  

2.1. Блок информации

Статистический показатель – одна из многих количественных характеристик статистической совокупности, численное выражение внутренней сущности изучаемого явления.

В зависимости от охвата единиц совокупности показатели подразделяются на индивидуальные, характеризующие отдельный объект и сводные, характеризующие группу объектов. Также статистические показатели можно классифицировать следующим образом:

• 
  абсолютные;
  
• 
  относительные;
  
• 
  средние.
  

Кроме того, для комплексной оценки здоровья населения, медицинской и экономической деятельности учреждений здравоохранения на основе математических моделей разрабатываются интегральные статистические показатели.

Абсолютные статистические показатели обладают определенной размерностью и единицей измерения, показывают количество, численность чего-то или кого-то, например, численность населения, число больничных коек, число врачей, число родившихся, число умерших, и др.

Относительные статистические показатели более объективно выражают количественные соотношения между явлениями. Для анализа здоровья населения и деятельности системы здравоохранения выделяют следующие группы относительных показателей:

• 
  экстенсивные показатели;
  
• 
  интенсивные показатели;
  
• 
  показатели соотношения;
  
• 
  показатели наглядности.
  

Экстенсивные показатели показывают внутреннюю структуру явления, разбиение его на составные части, удельный вес каждой части в целом. К экстенсивным показателям относятся структура заболеваемости, инвалидности, смертности, коечного фонда, врачебных специальностей и др. Рассчитывается показатель по следующей формуле и выражается в процентах (%).

Экстенсивный показатель =

Интенсивные показатели характеризуют уровень, распространенность какого - либо явления в среде, которое непосредственно связано с этой средой. Эти показатели рассчитываются, как правило, для анализа здоровья населения, где в качестве среды берется численность населения, а в качестве явления – число рождений, заболеваний, смертей и др. К интенсивным показателям относятся показатели заболеваемости, рождаемости, смертности населения и др. Рассчитывается показатель по следующей формуле и выражаются в промилле ( ), децимилле ( ), сантимилле ( ).

Интенсивный показатель =

Показатели соотношения характеризуют уровень (распространенность) какого-либо явления в среде, непосредственно (биологически) не связанного с данной средой. В этом их отличие от интенсивных показателей. Показатели соотношения рассчитываются, как правило, для анализа деятельности системы здравоохранения, ее ресурсного обеспечения, где в качестве среды берется численность населения, а в качестве явления – число врачей, средних медицинских работников, больничных коек, посещений амбулаторно-поликлинических учреждений и др. К показателям соотношения относятся обеспеченность населения стационарной, амбулаторно-поликлинической помощью, врачами, средними медицинскими работниками и др. Рассчитывается показатель по следующей формуле и выражаются в промилле ( ), децимилле ( ), сантимилле ( ).

Показатель соотношения =
Показатели наглядности применяются для анализа степени изменения изучаемого явления во времени и указывают, на сколько процентов или во сколько раз произошло увеличение или уменьшение сравниваемых показателей за данный период времени. Показатель наглядности получаем, как отношение ряда сравниваемых величин к исходной величине, принятой за 100 или за 1, результат получается либо в процентах, либо в долях. Как правило, за такую исходную величину берут начальные или конечные значения временного ряда.

Показатель наглядности =
2.2. Задания для самостоятельной работы

1. 
   Изучить материалы соответствующей главы учебника, модуля, рекомендуемой литературы.
   
2. 
   Ответить на контрольные вопросы.
   
3. 
   Разобрать задачу-эталон.
   
4. 
   Ответить на вопросы тестового задания модуля.
   
5. 
   Решить задачи для самостоятельного решения.
   

2.3. Контрольные вопросы

1. 
   Приведите классификацию статистических показателей.
   
2. 
   Дайте определение абсолютным статистическим показателям, приведите примеры.
   
3. 
   Дайте определение относительным статистическим показателям, приведите примеры.
   
4. 
   Перечислите виды относительных статистических показателей.
   
5. 
   Дайте определение экстенсивного показателя, приведите методику расчета и назовите область применения.
   
6. 
   Дайте определение интенсивного показателя, приведите методику расчета и назовите область применения
   
7. 
   Дайте определение показателя наглядности, приведите методику расчета и назовите область применения
   
8. 
   Дайте определение показателя соотношения, приведите методику расчета и назовите область применения
   
9. 
   Назовите различия между показателем соотношения и интенсивным показателем.
   
10. 
    Для чего необходимо графическое изображение полученных данных?
    
11. 
    Какие виды графиков используются для визуализации статистических показателей?
    

2.4. Задача-эталон

Исходные данные: среднегодовая численность населения некоторого субъекта РФ составляет 1 330 000 человек. В изучаемом году умерло 24 080 человек. Из этого числа 11 560 человек умерли от болезней системы кровообращения; 4 610 – от внешних причин; 3 730– от злокачественных новообразований; 1 445 – от болезней органов дыхания; 2 737 - от прочих причин. В городе развернуто 12 500 больничных коек, работает 4 200 врачей. При анализе коэффициента рождаемости за период 1995-2015 гг., установлено, что в 1995 г. этот показатель был равен 9,3, в 2000 г. - 8,7, в 2005 г. -10,2, в 2010 г. -12,6, в 2015 г. - 13,3 случаев на 1000 населения.
Задание

1. На основании представленных исходных данных необходимо рассчитать:

1.1. Экстенсивные показатели;

1.2. Интенсивные показатели;

1.3. Показатели соотношения;

1.4. Показатели наглядности.

2. Представить в графическом виде:

2.1. Экстенсивные показатели;

2.2. Интенсивные показатели;

2.3. Показатели наглядности.
Решение

1.1. Расчет экстенсивных показателей

1.1.1. Удельный вес умерших от болезней системы кровообращения
1.1.2. Удельный вес умерших от внешних причин
1.1.3. Удельный вес умерших от злокачественных новообразований
1.1.4. Удельный вес умерших от болезней органов дыхания
1.1.5. Удельный вес умерших от прочих причин

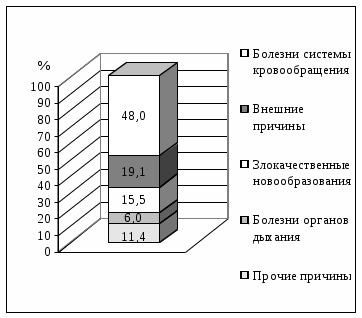
Вывод

В структуре смертности доля умерших от болезней системы кровообращения составила 48,0%, от внешних причин – 19,1%, от злокачественных новообразований – 15,5%, от болезней органов дыхания – 6,0%, от прочих причин – 11,4%. Данная структура смертности отличается от структуры причин смертности населения РФ.
2.1. Полученные данные можно представить в виде секторных диаграмм (круговой или столбиковой) с использованием прикладной компьютерной программы Microsoft Excel (рис. 2.1).

Рис. 2.1. Структура причин смерти в некотором субъекте РФ.

1.2. Расчет интенсивных показателей

1.2.1. Коэффициент общей смертности
1.2.2. Коэффициент смертности от болезней системы кровообращения
1.2.3. Коэффициент смертности от внешних причин
1.2.4. Коэффициент смертности от злокачественных новообразований
1.2.5. Коэффициент смертности от болезней органов дыхания
1.2.6. Коэффициент смертности от прочих причин

Вывод

Коэффициент общей смертности населения в некотором субъекте РФ составил 18,1 , наибольший уровень смертности от болезней системы кровообращения – 869,2 наименьший – от болезней органов дыхания – 108,6 . Эти данные превышают аналогичные показатели, сложившиеся в среднем по РФ.
2.2. Полученные данные можно представить в виде столбиковой диаграммы с использованием прикладной компьютерной программы Microsoft Excel. (рис. 2.2).


Рис. 2.2. Коэффициент смертности населения от различных причин (на 100 000 населения)

1.3. Расчет показателей соотношения

1.3.1.Обеспеченность населения больничными койками
1.3.2.Обеспеченность населения врачами

Вывод

Обеспеченность населения койками в медицинских организациях – 94,0 на 10 000 населения - соответствует среднероссийскому показателю. Обеспеченность населения врачами – 31,6 на 10 000 населения, что ниже среднего показателя по РФ.
1.4. Расчет показателей наглядности (на основе анализа динамики коэффициентов рождаемости за 2000-2015 гг.)
Значение показателя рождаемости в 1995 г. принимают за 100%. Тогда показатели наглядности за 2000-2015 гг. находят по следующим формулам:

для 2000 г.: ; для 2010 г.: ;

для 2005 г.: ; для 2015 г.:

Значения этих показателей можно выразить в долях, приняв величину показателя в 1995 году за 1. Результаты отражены в таблице 2.1.


Таблица 2.1. Показатели наглядности (на основе анализа динамики коэффициентов рождаемости за период 1995-2015 гг.).

Год	показатель рождаемости (на 1000 населения)	Показатель наглядности, %
1995	9,3	100
2000	8,7	80,7
2005	10,2	109,7
2010	12,6	135,5
2015	13,3	143,0

Вывод

Показатель рождаемости по отношению к 1995 г. в 2000 г. составил 80,7% (уменьшился на 19,3%), в 2005 г.- 109,7% (увеличился на 9,7%), в 2010 г. - 135,5% (увеличился на 35,5%), в 2015 г. составил 143,0% (увеличился на 43,0%).
2.3. Полученные данные представлены в виде линейной диаграммы с использованием компьютерной программы Microsoft Excel (рис. 2.3).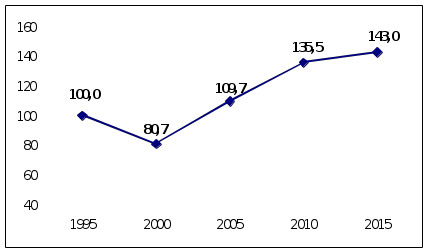



Рис. 2.3. Динамика коэффициента рождаемости (показатель наглядности, %)

за 1995-2015 гг.
2.5. Тестовые задания

Выберите только один правильный ответ.
1. Что такое абсолютнЫЙ СТАТИСТИЧЕСКИЙ ПОКАЗАТЕЛЬ?

1. Имеет определенную размерность и единицу измерения;

2. Дает качественную характеристику изучаемого явления;

3. Показатель, используемый для сравнения и сопоставления совокупностей;

4. Наиболее точный, достоверный показатель, характеризующий данное явление;

5. Показатель, используемый для обобщающей характеристики совокупности.
2. Какие показатели следует употреблять для характеристики частоты явления?

1. Соотношения;

2. Экстенсивные;

3. Интенсивные;

4. Наглядности;

5. Динамического ряда.
3. ДАЙТЕ ОПРЕДЕЛЕНИЕ ОТНОСИТЕЛЬНОГО СТАТИСТИЧЕСКОГО ПОКАЗАТЕЛЯ.

1. Показатель, характеризующий структуру явлений;

2. Показатель, выражающий количественное соотношение между явлениями;

3. Показатель взаимодействия двух величин;

4. Показатель, отражающий свойства генеральной совокупности;

5. Показатель, характеризующий размер количественных и качественных признаков.
4. Для чего используются экстенсивные показатели?

1. Чтобы наглядно показать различия сравниваемых групп;

2. Дать характеристику ряда, состоящего из однородных сопоставляемых величин;

3. Чтобы показать долю части в целом;

4. Чтобы судить о частоте явления;

5. Чтобы показать частоту явления в динамике.
5. НАЗОВИТЕ МЕТОДИКУ вычисления экстенсивного показателя:

1. Отношение числа, выражающего величину данного явления к величине всей совокупности;

2. Отношение значений двух самостоятельных совокупностей;

3. Отношение ряда чисел к одному из них, принимаемому за 100%;

4. Отношение абсолютного уровня последующего числа к предыдущему в %;

5. Отношение каждой последующей относительной величины к последующей в %.
6. НАЗОВИТЕ МЕТОДИКУ вычисления показателя наглядности:

1. Отношение числа, выражающего величину данного явления к величине всей совокупности;

2. Отношение части явления к целому явлению;

3. Отношение ряда сравниваемых однородных величин к одной из них, принятой за 100%;

4. Отношение абсолютного уровня последующего числа к предыдущему в %;

5. Отношение каждой последующей относительной величины к предыдущей в %.
7. Укажите, какому из приведенных ниже определений соответствует показатель соотношения:

1. Изменение явления во времени;

2. Распределение целого на части;

3. Уровень, распространенность явления в среде, непосредственно (биологически) не связанный с данной средой;

4. Сопоставление ряда однородных величин, имеющих разный характер;

5. Частота явления в среде, непосредственно с ним связанной.
8. Укажите, какому из приведенных ниже определений соответствует интенсивный показатель:

1. Изменение явления во времени;

2. Распределение целого на части;

3. Уровень, распространенность какого либо явления в среде, непосредственно связанного с этой средой;

4. Характеристика явления в среде, непосредственно с ним не связанной;

5. Сопоставление ряда однородных, но имеющих разный размер величин.
9. КАКОЙ ПОКАЗАТЕЛЬ МОЖНО ИСПОЛЬЗОВАТЬ ДЛЯ ИЗУЧЕНИЯ РАСПРЕДЕЛЕНИЯ БОЛЬНЫХ ПО ВОЗРАСТУ?

1. Интенсивный;

2. Экстенсивный;

3. Наглядности;

4. Соотношения;

5. Динамические ряды.
10. НАЗОВИТЕ ВИД СТАТИСТИЧЕСКОГО ПОКАЗАТЕЛЯ, ХАРАКТЕРИЗУЮЩИЙ ЧАСТОТУ СЛУЧАЕВ ЗАБОЛЕВАНИЙ СРЕДИ НАСЕЛЕНИЯ:

1. Экстенсивный;

2. Интенсивный;

3. Динамические ряды;

4. Соотношения;

5. Наглядности.
11. НАЗОВИТЕ ВИД СТАТИСТИЧЕСКОГО ПОКАЗАТЕЛЯ, ХАРАКТЕРИЗУЮЩИЙ ОБЕСПЕЧЕННОСТЬ НАСЕЛЕНИЯ КОЙКАМИ:

1. Интенсивный;

2. Экстенсивный;

3. Наглядности;

4. Соотношения;

5. Динамические ряды.

12. НАЗОВИТЕ ВИД СТАТИСТИЧЕСКОГО ПОКАЗАТЕЛЯ, ХАРАКТЕРИЗУЮЩИЙ СТРУКТУРУ ЗАБОЛЕВАЕМОСТИ:

1. Интенсивный;

2. Экстенсивный;

3. Наглядности;

4. Соотношения;

5. Динамические ряды.

13.ЧИСЛЕННОСТЬ НАСЕЛЕНИЯ ГОРОДА 150 000 ЧЕЛОВЕК. ВРАЧЕЙ 110. КАКОЙ ПОКАЗАТЕЛЬ МОЖНО РАССЧИТАТЬ ИЗ ПРИВЕДЕННЫХ ДАННЫХ?

1. Интенсивный;

2. Экстенсивный;

3. Соотношения;

4. Наглядности;

5. динамический ряд.
14. ИЗ 4000 ЗАБОЛЕВАНИЙ, ЗАРЕГИСТРИРОВАННЫХ В ПОЛИКЛИНИКЕ, 300 СЛУЧАЕВ - СЕРДЕЧНО-СОСУДИСТЫЕ ЗАБОЛЕВАНИЯ. КАКОЙ ПОКАЗАТЕЛЬ МОЖНО РАССЧИТАТЬ ИЗ ПРИВЕДЕННЫХ ДАННЫХ?

1. Интенсивный;

2. Экстенсивный;

3. Соотношения;

4. Наглядности;

5. Динамический ряд.
15. ЧИСЛЕННОСТЬ НАСЕЛЕНИЯ ГОРОДА 120 000 ЧЕЛОВЕК. ЗАРЕГИСТРИРОВАНО 5190 СЛУЧАЕВ ЗАБОЛЕВАНИЙ. КАКОЙ ПОКАЗАТЕЛЬ МОЖНО РАССЧИТАТЬ ИЗ ПРИВЕДЕННЫХ ДАННЫХ?

1. Интенсивный;

2. Экстенсивный;

3. Соотношения;

4. Наглядности;

5. Динамический ряд.
2.6. Задачи для самостоятельного решения

Задача 1

Исходные данные: среднегодовая численность населения некоторого субъекта РФ составляет 1 170 850 человек. В изучаемом году впервые зарегистрировано 738 550 случаев заболеваний. Из числа всех зарегистрированных заболеваний 365 950 - болезни органов дыхания, 97 045 – травмы, отравления и некоторые другие последствия воздействия внешних причин, 58 975 – болезни кож, 55 350 – болезни костно-мышечной системы, 161 230 – прочие болезни. На территории субъекта развернуто 12 920 коек, работает 4 245 врачей. При анализе первичного выявления случаев ВИЧ – инфицирования за 1995–2015 г.г. установлено, что в 1995 г. зарегистрировано 18 случаев, в 2000 г. – 40, в 2005 г. – 75, в 2010 г. – 176, в 2015 г. – 340 случаев.
Задача 2

Исходные данные: среднегодовая численность населения трудоспособного возраста некоторого субъекта РФ составляет 625 615 человек. В изучаемом году умерло 6 540 человек. Из числа всех умерших 2 350 человек умерли от болезней системы кровообращения; 2 480 – от внешних причин; 635 – от злокачественных новообразований; 395 – от болезней органов пищеварения; 680 - от прочих причин. На территории субъекта развернуто 9750 коек, работает врачей - 4980. При анализе показателя смертности населения за 1995 – 2015 гг., установлено, что в 1995 г. показатель был равен 15,2, в 2000 г. – 15,7, в 2005 г. – 16,3, в 2010 – 14,3, в 2015 г. –18,7 случаев на 1000 населения.
Задача 3

Исходные данные: среднегодовая численность взрослого населения некоторого субъекта РФ составляет 548 415 человек. В изучаемом году впервые признано инвалидами 8269 человек. Из числа признанных инвалидов 3807 человек стали инвалидами от болезней системы кровообращения; 1370 – от злокачественных новообразований; 1085 – от болезней костно-мышечной системы и соединительной ткани; 876 - от последствий травм, отравлений и некоторых других последствий воздействия внешних причин, 1131 - от прочих причин. На территории субъекта развернуто 6750 коек, работает врачей - 2380. При анализе показателя смертности от болезней органов пищеварения среди мужского населения за 1995–2015 гг. установлено, что в 1995 г. показатель был равен 60,0, в 2000 г. - 63,3, в 2005 г. – 103,6, в 2010 г. – 124,0, в 2015 г. – 111,6 случаев на 100 000 мужского населения.
Задание

1. На основе представленных исходных данных в задачах 1,2,3 необходимо рассчитать:

1.1. Экстенсивные показатели;

1.2. Интенсивные показатели;

1.3. Показатели соотношения;

1.4. Показатели наглядности

2. Представить в графическом виде:

2.1.Экстенсивные показатели;

2.2.Интенсивные показатели;

2.3.Показатели наглядности
2.7. Рекомендуемая литература

1. 
   Медик В.А. Общественное здоровье и здравоохранение: учебник. – 3-е изд., испр. и доп. – М.: ГЭОТАР-Медиа, 2017.
   
2. 
   Медик В.А., Токмачев М.С. Математическая статистика в медицине: учеб. пособие. - М.: Финансы и статистика, 2007. – 800 с.
   

Модуль 3. Средние величины

Цель изучения модуля: показать значение средних величин для изучения общественного здоровья, деятельности системы (организаций) здравоохранения и в клинической практике.
После изучения темы студент должен знать:

• 
  виды средних величин;
  

• 
  способы вычисления средних величин.
  

Студент должен уметь:

• 
  рассчитывать и анализировать среднюю арифметическую;
  
• 
  применять среднюю арифметическую в конкретной ситуации для анализа общественного здоровья, деятельности организаций здравоохранения;
  
• 
  использовать полученные знания при обучении на клинических кафедрах.
  

3.1. Блок информации
В медико-социальных исследованиях наряду с абсолютными и относительными показателями используются средние величины, которые характеризуют весь ряд наблюдений одним числом.

Для расчета средних величин необходимо соблюдать следующие условия:

• 
  средние величины должны быть рассчитаны на основе качественно однородных статистических групп;
  
• 
  средние величины исчисляются на совокупностях, имеющих достаточно большое число наблюдений.
  

В медико-социальных исследованиях используются следующие виды средних величин:

• 
  средняя арифметическая;
  
• 
  средняя арифметическая взвешенная;
  
• 
  средняя гармоническая взвешенная;
  
• 
  средняя геометрическая невзвешенная;
  
• 
  средняя геометрическая взвешенная;
  
• 
  средняя квадратическая невзвешенная;
  
• 
  средняя квадратическая взвешенная.
  

К средним величинам относят математическое ожидание, а также моду, как наиболее типичное значение, имедиану, как середину распределения случайной величины.

При изучении общественного здоровья, анализе деятельности медицинских организаций, оценки работы медицинского персонала из всех видов средних величин наиболее часто используются средняя арифметическая, которая может быть простой и взвешенной.

Последовательность наблюдений (выборка объема ), все элементы которой упорядочены по возрастанию, называется вариационным рядом. Элемент вариационного ряда – варианта. Каждое из значений в выборке может встречаться неоднократно, количество одинаковых вариант для каждого называется его частотой . Если число различных значений в выборке обозначить , где , то .

Соответственно величина называется относительной частотой для значения . Обязательно, . Множество выборочных значений и соответствующих им относительных частот называется выборочным (статистическим) распределением:

			…
			…

Средняя арифметическая простая – средняя вариационного ряда , где каждая варианта записана столько раз, сколько встречается. Вычисляется по формуле

.

Среднюю арифметическую значений можно записать иначе, с учетом частоты повторений каждого из значений. Получаем среднюю арифметическую взвешенную вариационного ряда, где k различных значений, k≤n.