Организация перевозок грузов в универсальных контейнерах из Могилева в Нижний Новгород (на примере деятельности ооо "МоготексАдонис")
 Скачать 2.05 Mb. Скачать 2.05 Mb.
|
|
Допустимые варианты загрузки автомобилей
На первом этапе формируются все возможные варианты загрузки автомобиля комбинацией из двух грузов. Все они удовлетворяют необходимому условию (табл. 9). Затем продолжается процесс формирования вариантов загрузки из трех грузов. Очевидно, что все варианты, включающие груз с номером 7 и выше, из дальнейшего рассмотрения следует исключить, что существенно сокращает количество рассматриваемых вариантов. Комбинации из четырех грузов не удовлетворяют необходимому условию и поэтому также исключаются из рассмотрения. Процесс расчеты продолжается до тех пор, пока не будут рассмотрены все возможные исходные номера грузов. В табл.8 и табл.9 находится комбинация (или несколько комбинаций), для которой 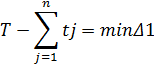 (9) (9)Грузы, входящие в найденную комбинацию, исключаются из рассмотрения. В анализируемом примере наименьшая невязка между потребными затратами времени на перевозку и временем нахождения автомобиля в наряде имеет место для комбинации грузов 9,10 и равна Δ1=480-474=6мин. В оставшейся части таблиц исключаются варианты, содержащие грузы 9 и 10, и пункт 3 повторяется Ʀ раз до тех пор, пока не будет найдено допустимое решение. В частности, после исключения вариантов с груза 9 и 10 наименьшее значение критерия Δ=7 характерно для следующих комбинаций: 1,3, 4; 1, 3, 5; 1,3,6; 1,4,5; 1,4,6; 1,5,6; 2,3,4; 2,3,5; 2,3,6; 2,4,5; 2,4,6; 2,5,6. Выбираем любые из комбинаций, не содержащих грузы с одноименными номерами. Такими, например, являются:1,3,4; 2,5,6 или 1,3,5; 2,4,6 и т.д. В оставшейся части таблицы осталась только одна комбинация 7,8, для которой Δ = 16. Это свидетельствует о том, что оптимальный план перевозок составлен(табл.10.). Для перевозки груза достаточно иметь четыре автомобиля, так как ∑tj= 474+473+473+464=1884< 1920 первый автомобиль должен работать на маршруте, включающем две ездки со склада к третьему потребителю: время работы автомобиля на маршруте составляет 474 мин. Второй автомобиль необходимо использовать для выполнения одной ездки к первому потребителю и двух к четвертому. При этом время работы на маршруте составляет 473 мин. Третий автомобиль должен совершить одну ездку к первому и две к четвертому, затратив 473 мин. Наконец, четвертый автомобиль целесообразно использовать для доставки грузов со склада второму потребителю, затратив на это 464 мин. Таблица 10 Оптимальный план закрепления автомобилей за потребителями
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
