ОСНОВЫ работы в MathCad. Основы работы в математическом пакете Mathcad
 Скачать 8.94 Mb.
|
8.2. Программирование функцийДля написания программ-функций в системе MathCAD предусмотрена специальная панель программироваия – Programming (Программирование), содержащая все операторы и элементы языка. Общий вид панели Programming представлен на рис. 8.2. Операторы в программу вставляются только с помощью кнопок этой панели. Назначение основных команд, представленных на панели:
Рис.7.2. Вид панели инструментов Programming (Программирование) Чтобы написать программу, прежде всего для нее должен быть создан специальный, обособленный от остального документа, программный блок-тело функции. Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения и операторы алгоритма. Чтобы построить единичный элемент программного блока, нажмите кнопку команды Add Line (Добавить линию) панели Programming (Программирование). Присваивание значений в программах имеет ряд особенностей. Важнейшим из них является то, что присвоение величин используемым алгоритмом функциям и переменным может быть произведено как в самой программе, так и выше нее. Данные два подхода весьма существенно разнятся:
Все программы составляемые в пакете MathCAD с точки зрения любого языуа программирования (например, Turbo Pascal) представляют собой подпрограммы – функции, которые могут возвращать в качестве результата число, вектор или матрицу. 8.3. Описание программы-функцииПеред тем как использовать программу-функцию нужно ее описать. Описание программы-функции размещается в рабочем документе перед вызовом программы-функции и включает в себя заголовок функции и тело функции, соединенные в единое целое с помощью операции присваивания («:=»). Заметим, что если программа используется для вычисления одного значения, то в своем заголовке она не содержит списка формальных параметров и называется программой-скаляром. Программа-функция может не иметь формальных параметров и тогда, когда данные передаются через имена переменных, определенных выше описания программы-функции. Эти переменные будут являться глобальными для данной функции. Технология создания программы-функции в рабочем документе MathCAD состоит из следующих шагов:
Пример 1. Требуется подготовить описание функции  и вычислить значения этой функции при x= 4.15 и g= 1.854. Решение. Заметим, что при вычислении y можно обойтись без описания и использования пользовательской функции и тем более без программирования, как это показано на рис. 8.4, a. Использование функции следует из требования к задаче для простоты изложения. Для нахождения значения функции «внутрь» программы-функции следует передать значения x и g, необходимые для выполнения вычислений внутри программы. Поэтому переменные x и g следует включить в список формальных параметров заголовка создаваемой функции. Назовем эту функцию – y. Тогда подготовка описания функции, и ее выполнение в соответствии с описанной технологией могут быть выполнены, как это представлено на рис. 8.3.
Рис.7.3. Пошаговое создание и выполнение программы-функции В данном примере введена вспомогательная локальная переменная t для вычисления значения функции. И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 8.4, b, c приведены другие варианты решения поставленной задачи.
Рис. 8.4. Демонстрация элементов программирования простых выражений В примере, представленном на рис. 8.4, в первой колонке a для вычисления значения  используется базовый набор средств без элементов программирования. Во второй b и третьей c колонках производятся точно такие же вычисления, но с использованием элементов программирования. Обе программы (b и c) можно считать эквивалентными, так как возвращают они одно и то же значение, которое располагается в последней строчке программируемой части. В (b и c) мы имеем дело с программой – скаляром, так как они используются для вычисления одного значения и не имеют формальных параметров.Внутри программ (bи c) используются глобальные переменные g и x из документа. Значения этих переменных определены заранее. Обе программы из примера, представленного на рис. 8.4, в своей программируемой части содержат операторы присваивания с использованием локальных переменных. Переменные, созданные внутри программы с таким видом присваивания, являются внутренними, и доступ к ним может осуществляться только в самой программе.
Пример 2. Требуется найти действительные корни квадратного уравнения 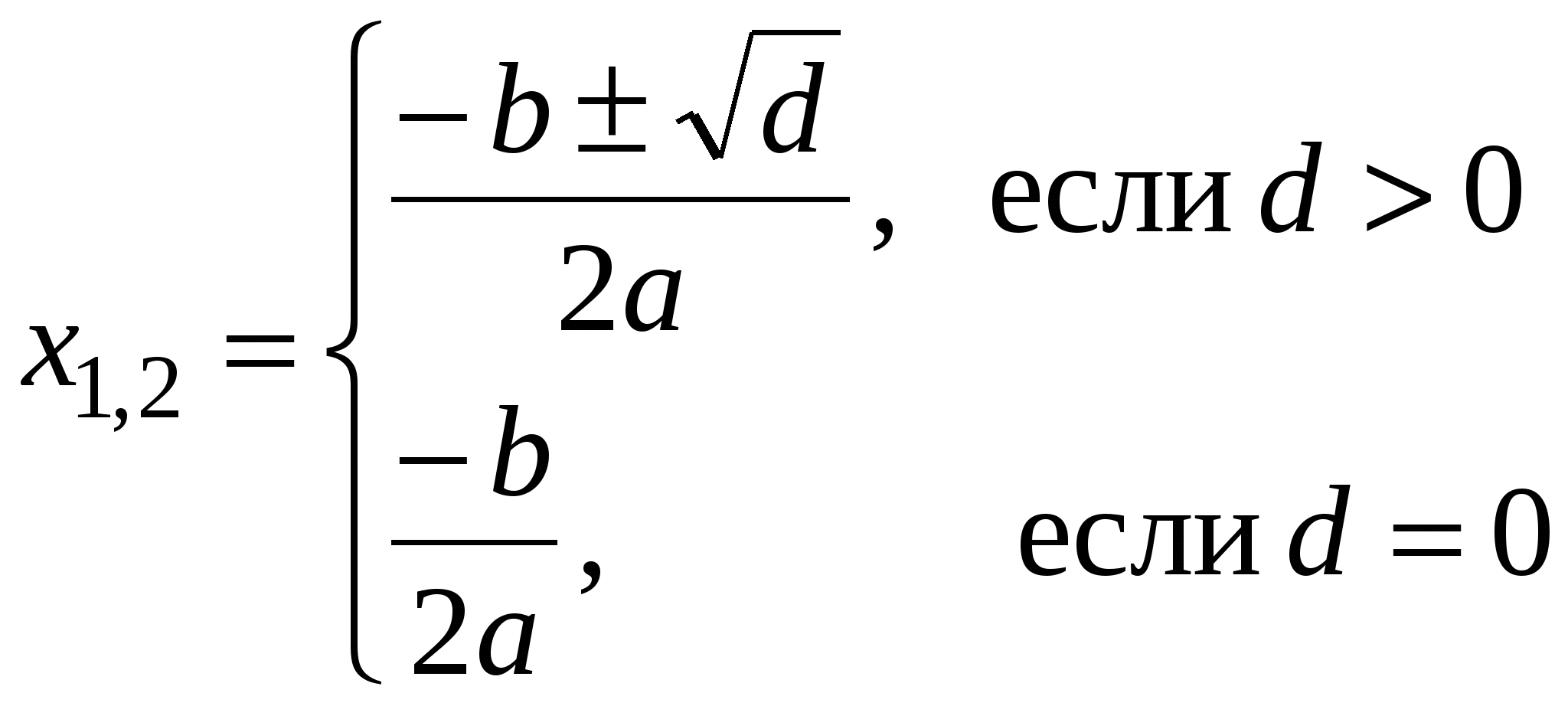 , где a, b, c– любые действительные числа и  . Известно, что в зависимости от знака дискриминанта  действительные корни уравнения могут быть получены по формуле: Блок-схема этого алгоритма показана в главе 1 на рис. 1.2. Решение. Опишем вычисление корней в виде программы-функции. Спецификацию для этой функцииможно записать следующим образом. Функция R(a,b,с) возвращает значения действительных корней квадратного уравнения  или сообщает о том, что уравнение не имеет корней. Здесь a, b, с – коэффициенты уравнения.Очевидно, что в данном случае мы имеем дело с ветвящимся процессом. Программирование ветвящихся процессов требует проверки некоторых условий, в зависимости от которых выбирается вычислительная формула. Для реализации таких вычислений на панели программирования предусмотрен оператор if (если). 
if .
Описание функции и примеры ее вызова представлены на рис. 8.5. 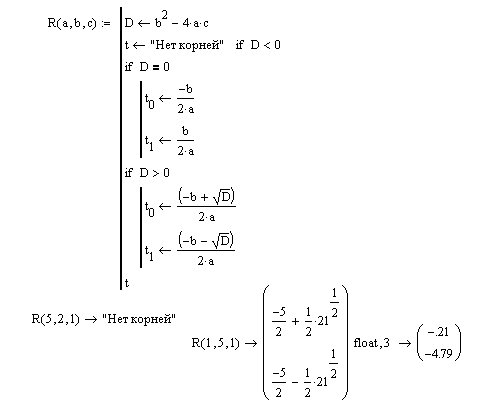 Рис. 8.5. Описание функции R(a,b,x), предназначенной для вычисления корней квадратного уравнения Пример 3. Требуется подготовить описание программы-функции 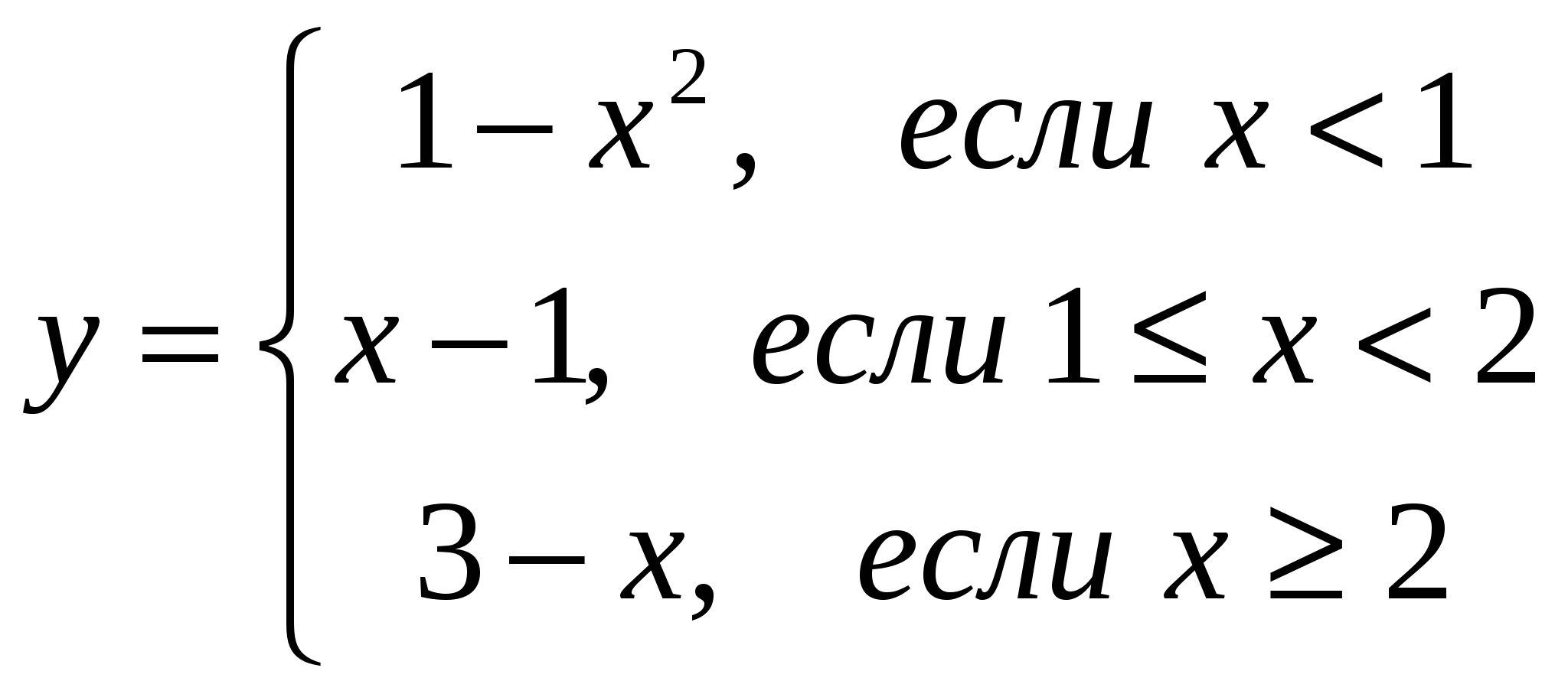 и построить ее график на интервале [–2, 4] . Решение. Из анализа аналитического выражения функции y видно, что функция является кусочно-непрерывной на числовой оси и алгоритм вычислений содержит три ветви. Вычисление значения y зависит от местоположения переменной x на числовой оси. Для нахождения значения функции целесообразно ввести один формальный параметр, соответствующий переменной x. Спецификацию для этой функции можно записать следующим образом: Функция f(x) возвращает значение функции, определенной в соответствии с условием примера 3. Здесь х – аргумент для вычисления. В описании функции требуется проверить три условия. В зависимости от результатов проверки этих условий применяется соответствующая условию вычислительная формула. Поэтому при программировании можно с проверкой каждого из условий связать условный оператор if, как это показано на рис. 8.6. А можно ограничиться проверкой двух условий и оператором otherwise, учитывая тот факт, что функция задана на всей числовой оси, и исключение двух условий оставляет выполнение третьего условия. На рис. 8.7 представлен второй вариант функции-программы. 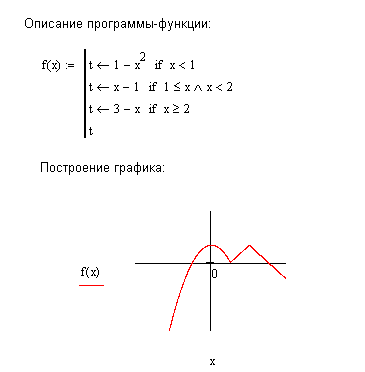 Рис. 8.6. Демонстрация элементов программирования ветвящихся процессов  Рис. 8.7. Демонстрация элементов программирования ветвящихся процессов На рис. 8.8 представлены примеры программ-функций, реализующих вычисления, содержащие ветвящиеся процессы.
Рис. 8.8. Примеры программирования функций с проверкой условий. Здесь x – глобальная переменная Пример 4. Требуется найти максимальный и минимальный элементы в заданном массиве. Решение. Задача поиска наибольшего/наименьшего значений в заданном массиве относится к типовым циклическим алгоритмам и подробно описана в главе 1, а на рис.1.9 и 1.10 приведены блок-схемы этих алгоритмов. Спецификацию для этой функцииможно записать следующим образом: Функция Fun(P) возвращает наибольшее и наименьшее значение в массиве Р. Для создания циклов в MathCAD предусмотрено два оператора: for и while. Поскольку количество повторений цикла заранее известно и связано с числом элементов заданного массива, в данном решении целесообразно использовать оператор for.
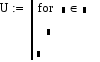 Рис. 8.9. Шаблон оператора цикла for
Обозначим имя переменной-счетчика, которая используется в оператореfor – буквой t. Для описания алгоритма воспользуемся тем, что в операторе цикла для переменной-счетчика можно указать в качестве диапазона имя массива. Как сказано выше, в таком случае переменнаяt будет последовательно принимать значения всех элементов указанного в for массива (в нашем случае – это массив Р). Для обозначения максимального и минимального значений в программу введем две вспомогательные переменные Pmax и PMin. Тогда описание функции может быть представлено в виде, как это показано на рис. 8.10. Отметим, что в данном случае в качестве результата работы функции нужно вернуть два значения, а специфика функции в MathCAD такова, что она позволяет вернуть только одно значение, но при этом сказано, что функция в качестве результата может вернуть, в том числе, вектор и матрицу. Поэтому при формировании результата мы определим его как вектор из двух значений. Справа от программы-функции, представленной на рис. 8.10, написаны операторы, предназначенные для создания вектора с именем U из шести элементов. Для этого введена вспомогательная переменная i, задающая диапазон изменения индекса массива, а значения элементов массива U формируются с помощью функции rnd – датчика случайных чисел. Параметр 20 в ней определяет диапазон принимаемых значений. На рис. 8.11, a представлен второй вариант программы-функции, в котором в качестве диапазона значений для переменной-счетчика цикла for берется диапазон изменения индекса массива. Поэтому в список формальных параметров в заголовок функции вносится еще один параметр n, который указывает верхнюю границу изменения индекса.  Рис. 8.10. Описание и использование функции Fun(P)
Рис. 8.11. Описание и использование функции Fun(P) |
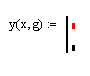
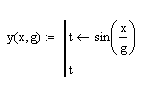
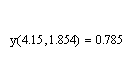
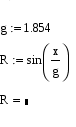
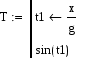
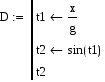
программной части используются глобальные переменные обычно только как операнды в выражениях. 
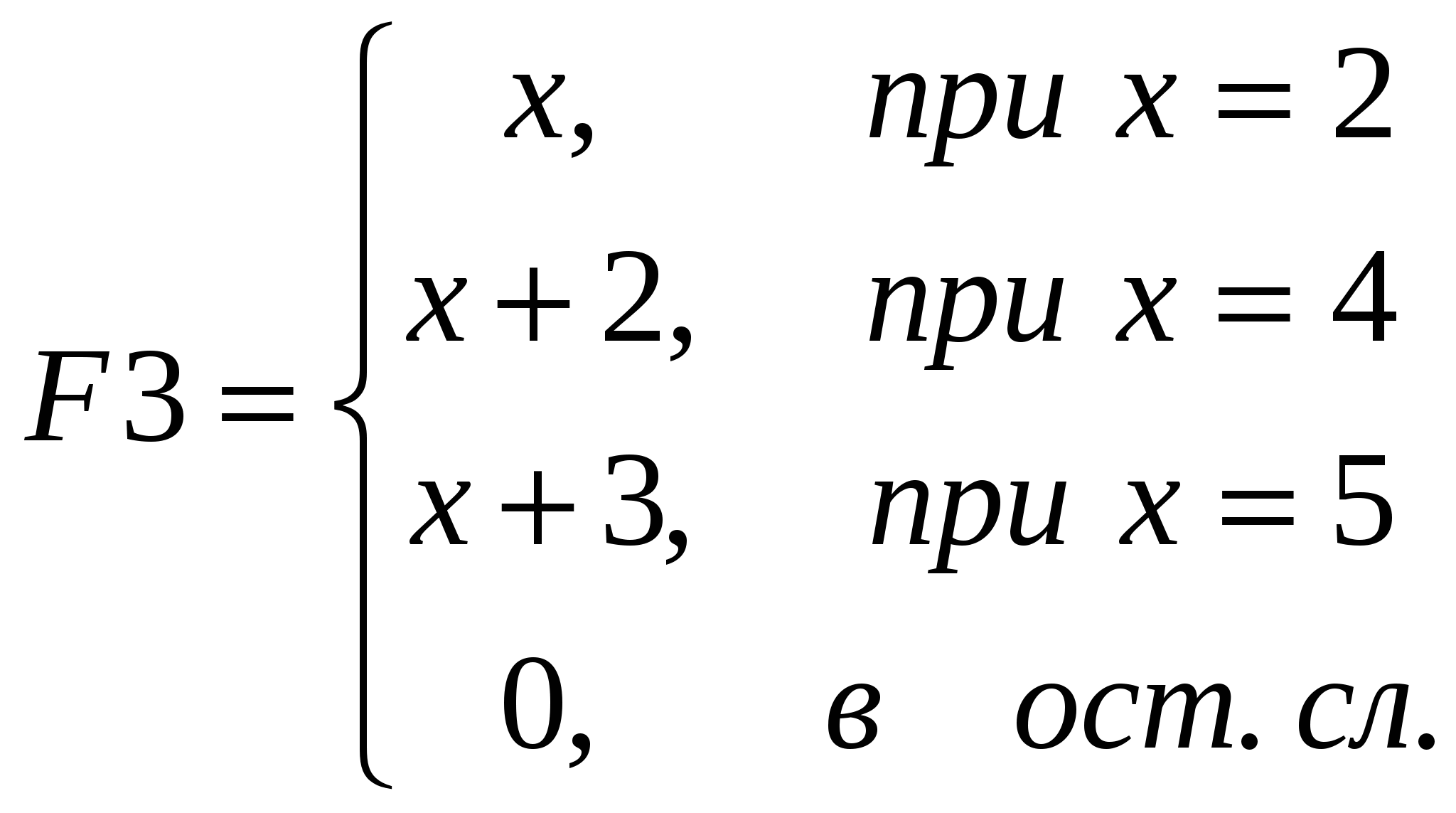
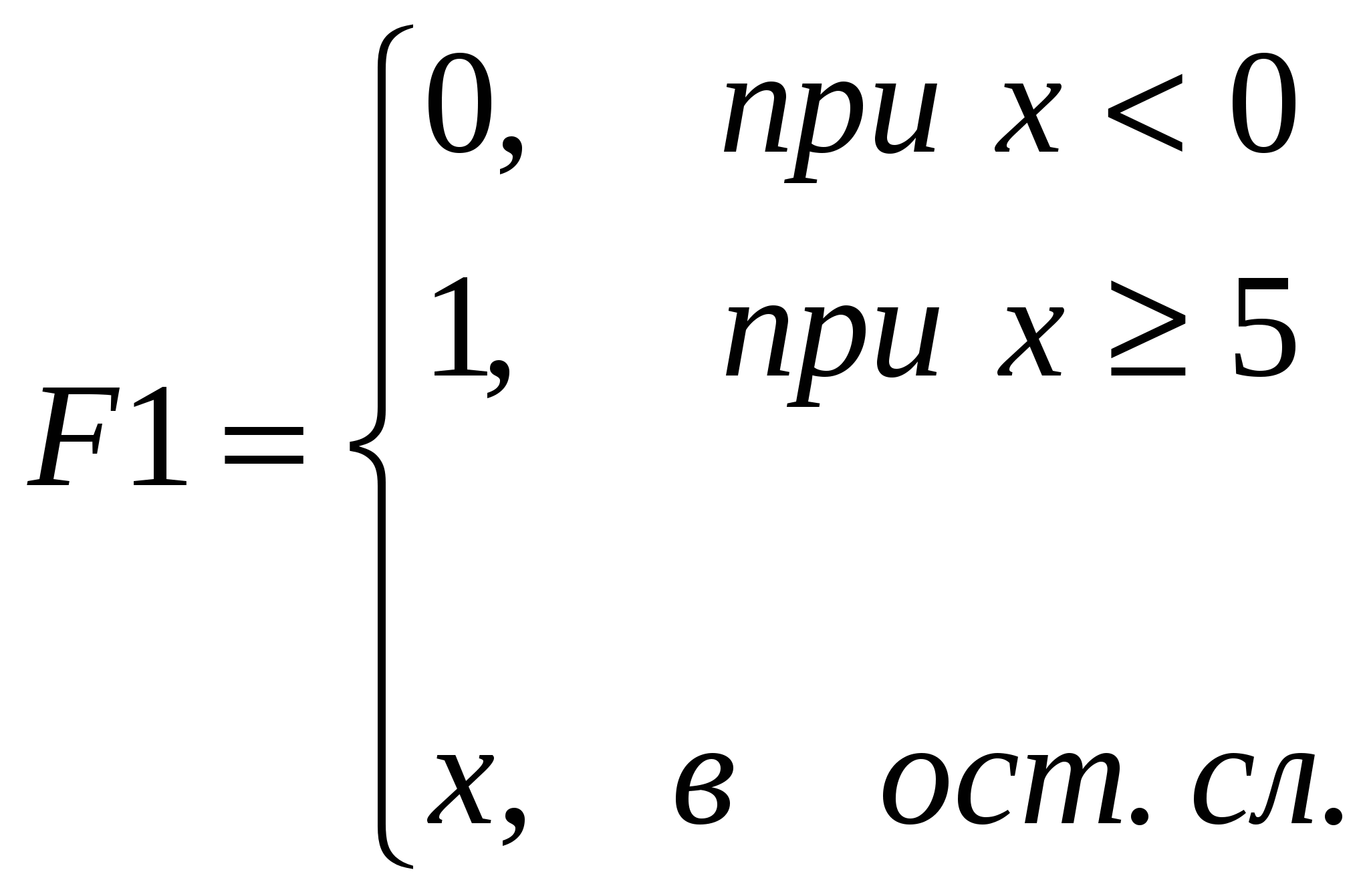
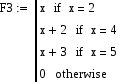
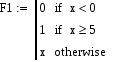
осле вставки оператора for в строку 
