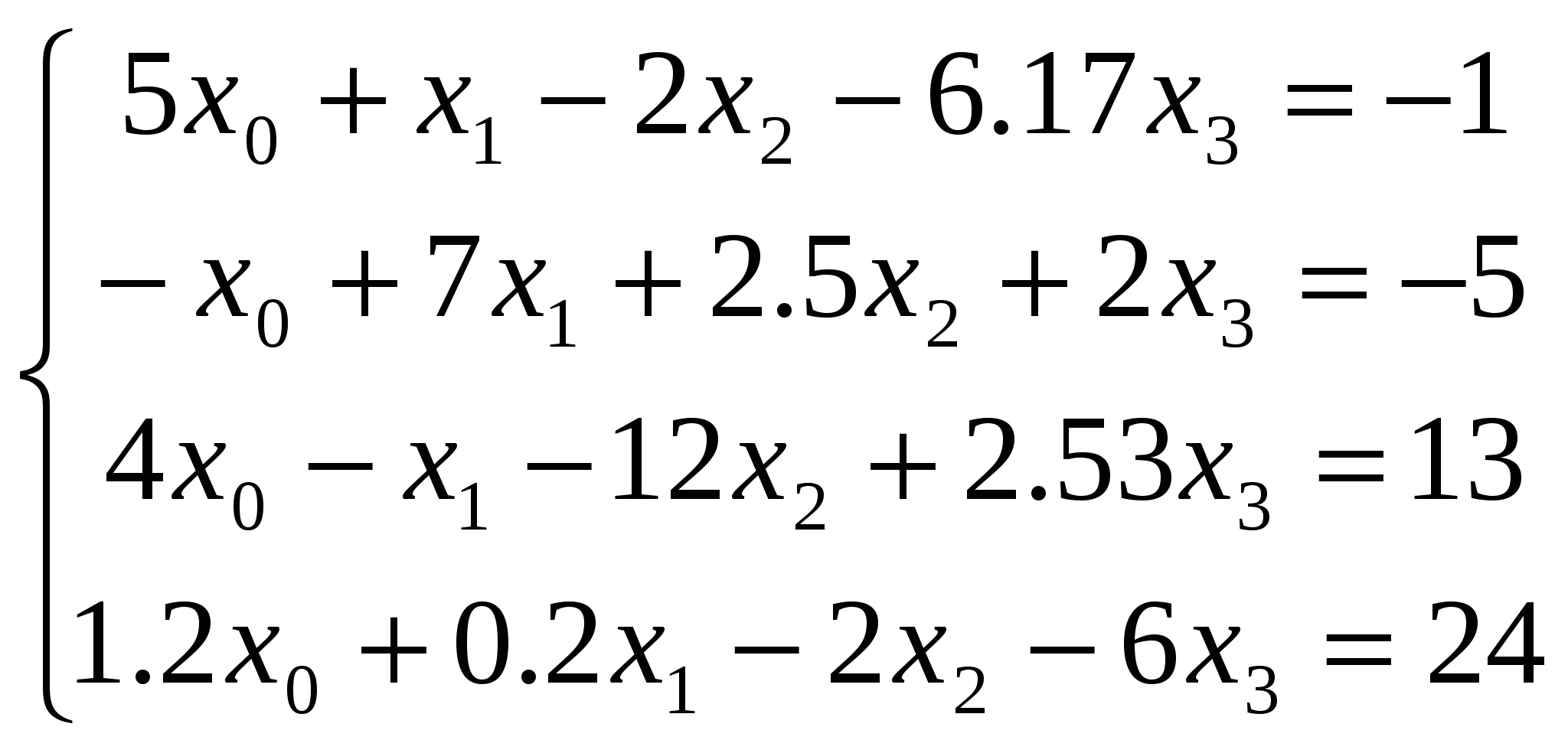|
|
ОСНОВЫ работы в MathCad. Основы работы в математическом пакете Mathcad
7.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований
Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:
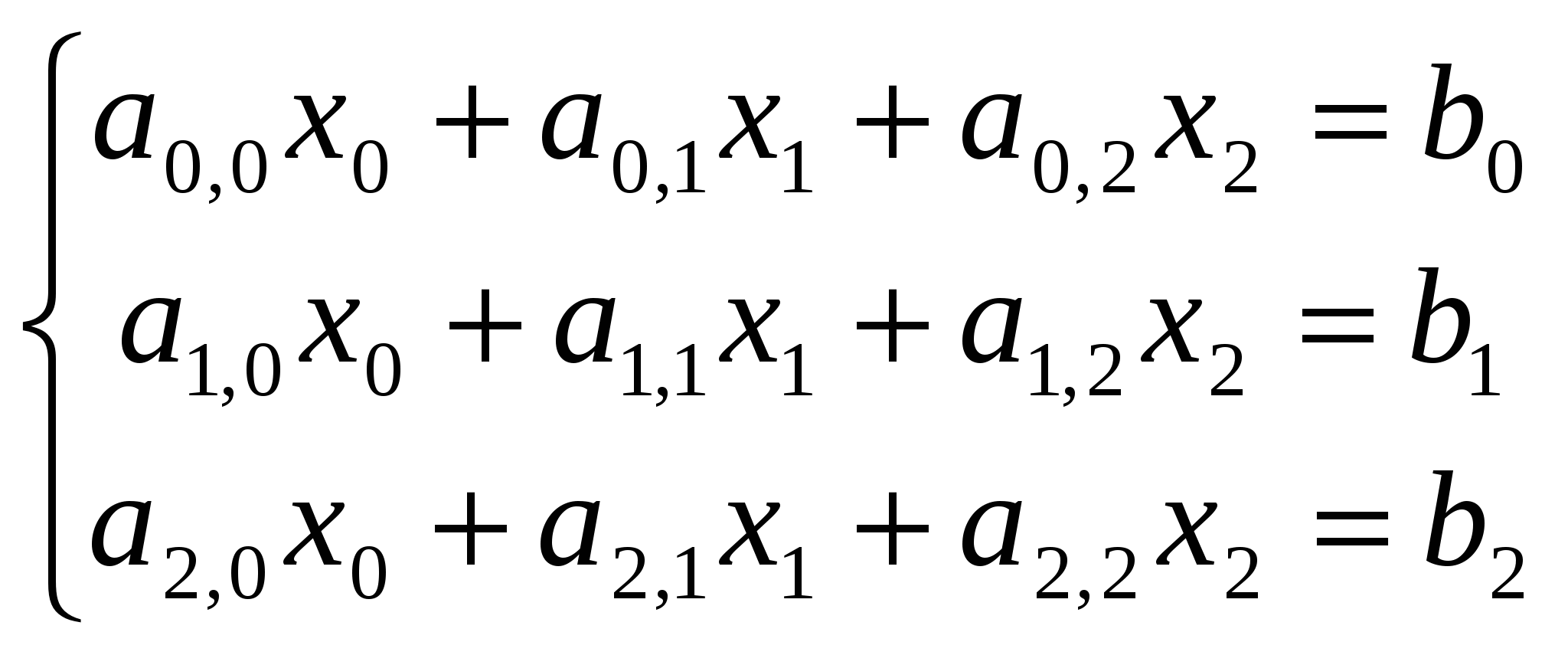 (7.1) (7.1)
Введем следующие обозначения:
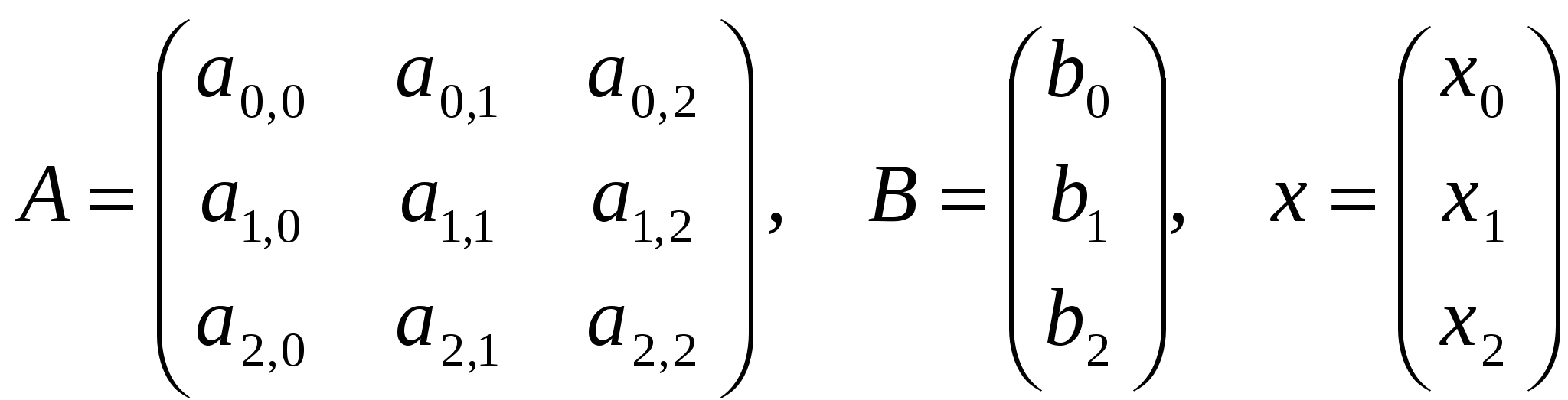 , (7.2) , (7.2)
здесь:
А – матрица коэффициентов;
В – вектор свободных членов;
х – вектор неизвестных.
В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:
Ax=B. (7.3)
Из линейной алгебры известно, что система (7.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.
В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (7.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:
Помножим уравнение (7.3) слева на матрицу, обратную к матрице А:
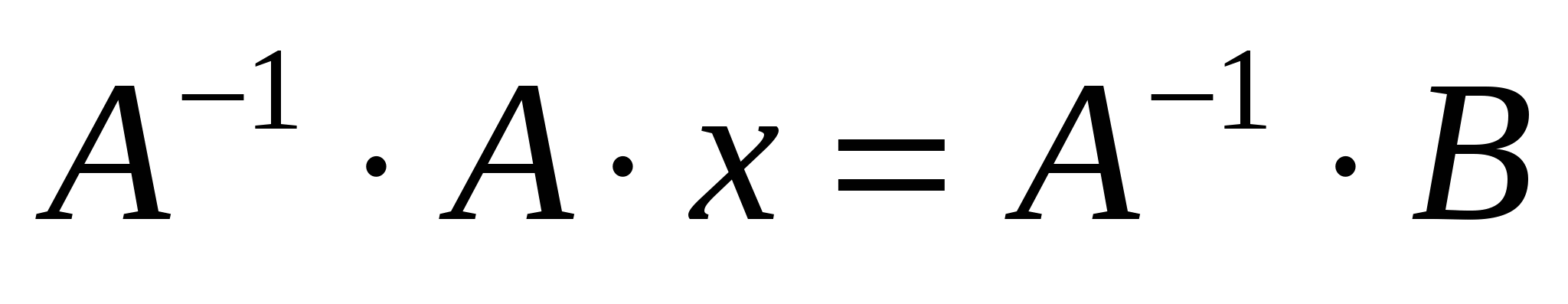 . (7.4) . (7.4)
Воспользуемся свойством, что  , где Е – единичная матрица. Тогда уравнение (7.4) примет вид: , где Е – единичная матрица. Тогда уравнение (7.4) примет вид:
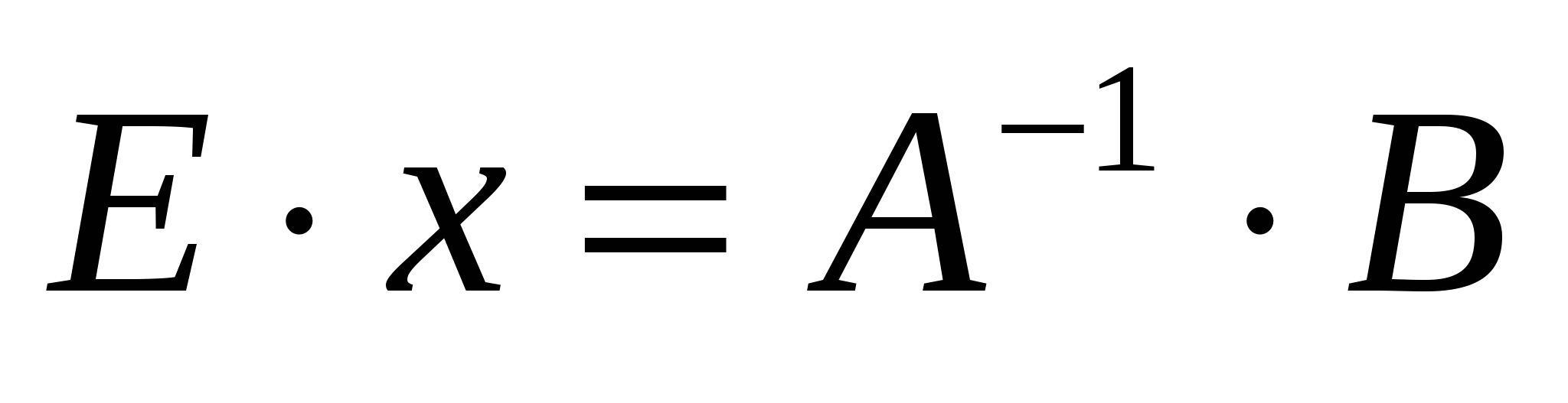 . (7.5) . (7.5)
Воспользуемся свойством, что Ex = x. Тогда уравнение (7.5) примет вид:
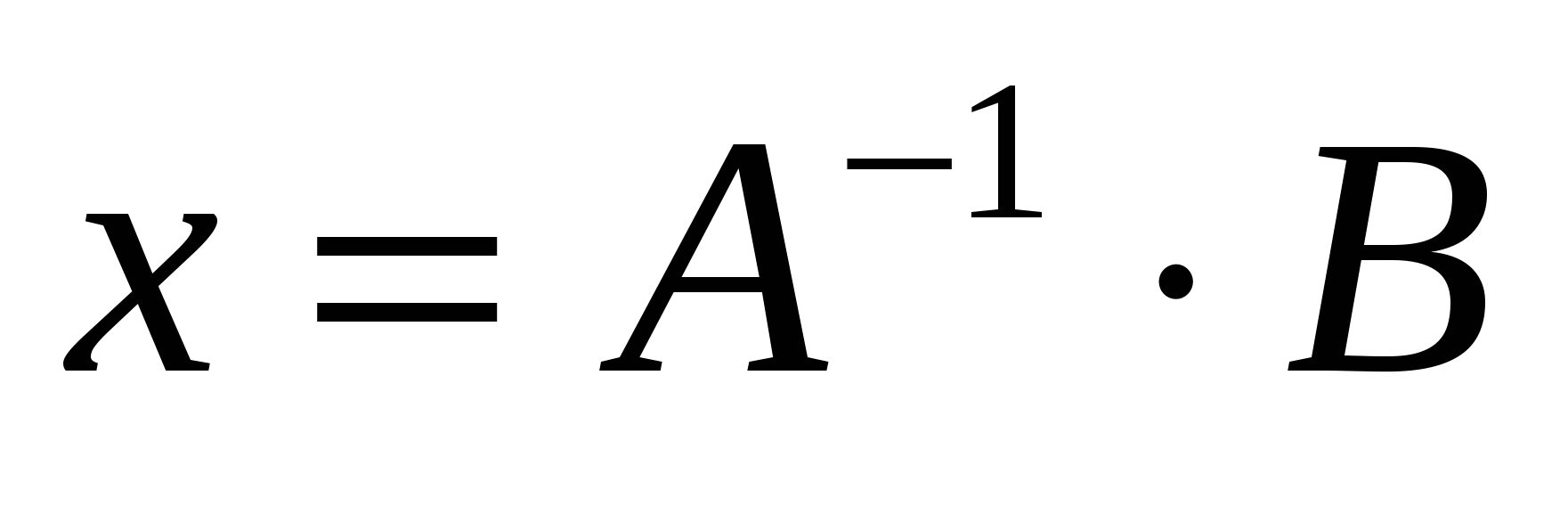 , (7.6) , (7.6)
где (7.6) – решение системы (7.3).
Пример 15. Требуется найти решение следующей системы линейных уравнений:
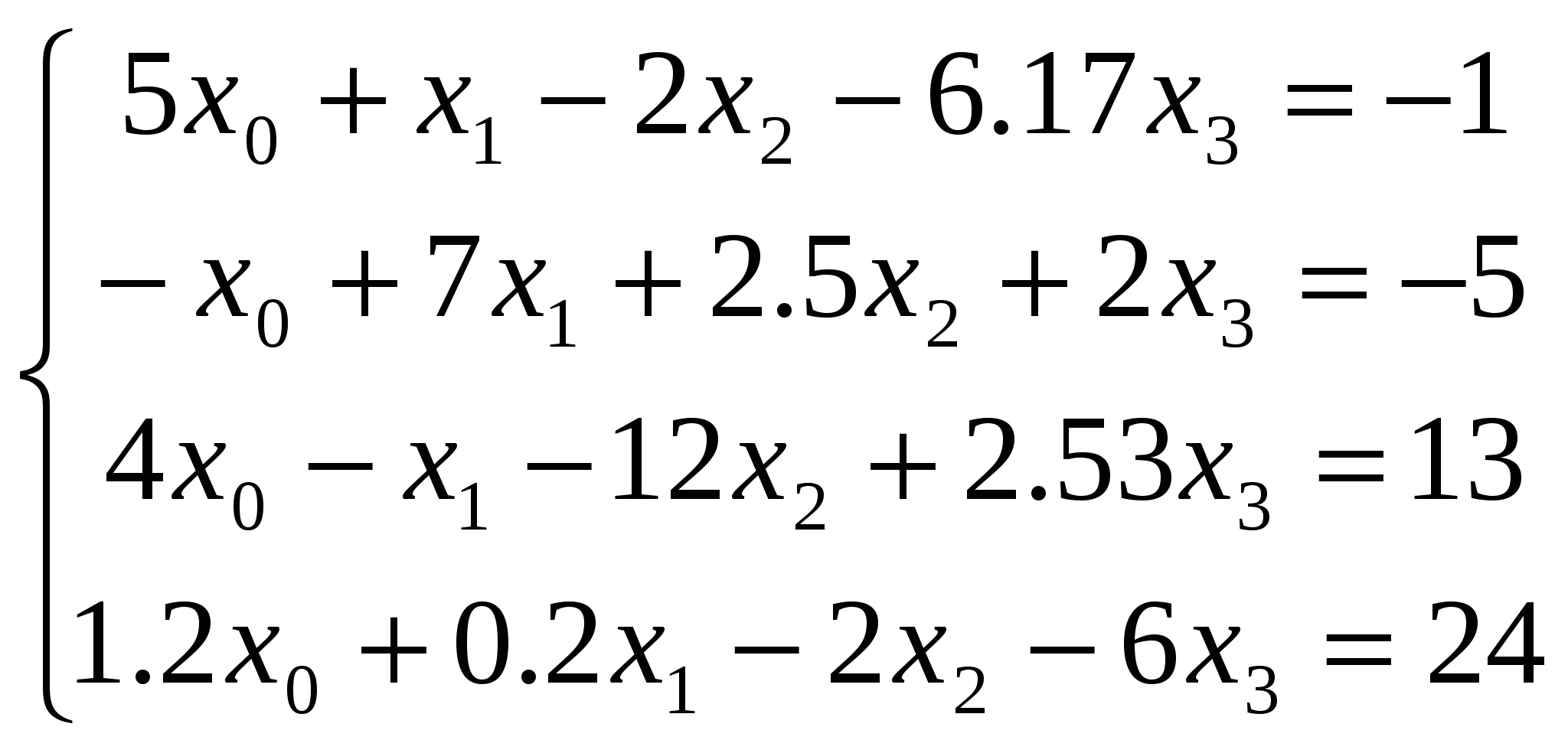
Решение. Решение СЛАУ матричным способом в системе
MathCAD приведено на рис.7.13.


Рис. 7.13. Решение СЛАУ пакете MathCAD
Глава 8
ПРОГРАММИРОВАНИЕ В СИСТЕМЕ MATHCAD
Функции являются важнейшим инструментом математики. В разделе 5.9 технология работы с пользовательскими функциями, которые можно описать с помощью одного выражения. Если описания функции нельзя уместить в одно выражение, то без элементов программирования обойтись сложно.
Язык программирования MathCAD содержит все элементы языка высокого уровня, необходимые для математических расчетов. Будучи дополненным сотнями встроенных функций и операторов системы, возможностями численного и символьного расчета различных величин, он по эффективности не уступает профессиональным системам программирования. Кроме того, у него есть одно очень крупное преимущество: язык программирования MathCAD предельно прост (а по изящности и наглядности в оформлении алгоритмов вообще не имеет аналогов).
Как правило, при использовании функций, встроенных в систему MathCAD, пользователи не задумываются о том, на основании каких методов и решений достигается цель, поставленная перед функцией. Такая встроенная функция используется по типу «черного ящика» – пользователь познакомился с ее описанием/спецификацией, вызвал для решения, получил ответ.
При программировании пользовательских функций будем придерживаться «созвучного» порядка, т.е. идти от спецификации к программированию.
8.1. Спецификации функций
Спецификация функции состоит из ее заголовка и описания назначения – выходного значения или результата работы функции. Для примера можно обратиться к мастеру функций и более внимательно посмотреть на предоставляемые им для его функций описания. На рис. 8.1 открыта страница со спецификацией функции rnorm.
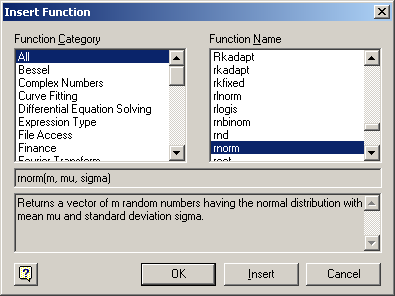 
Рис. 8.1. Спецификация функции, предоставляемая мастером функций
Заголовок содержит имя функции (rnorm) и список формальных параметров(m, mu, sigma). Каждая пользовательская программа-функция MathCAD должна иметь оригинальное имя, используя которое будет осуществляться обращение к этой программе-функции. Через это же имя (и только через это имя ) «возвращается» в рабочий документ результат выполнения программы-функции.
Через формальные параметры «внутрь» программы-функции «передаются» данные, необходимые для выполнения вычислений внутри программы. В качестве формальных параметров могут использоваться имена простых переменных, массивов и функций. Формальные параметры отделяются друг от друга запятой.
При описании назначения функции необходимо сказать, что возвращает функция в качестве своего результата (в описываемой функции rnorm возвращает вектор нормально распределенных случайных значений). При этом обязательно нужно пояснить роль каждого из формальных параметров, перечисленных в заголовке (m – количество значений, mu – среднее значение, sigma – стандартное отклонение). Желательно сказать об ограничениях, т.е. невозможность расчета при … каких-либо условиях.
|
|
|
 Скачать 8.94 Mb.
Скачать 8.94 Mb.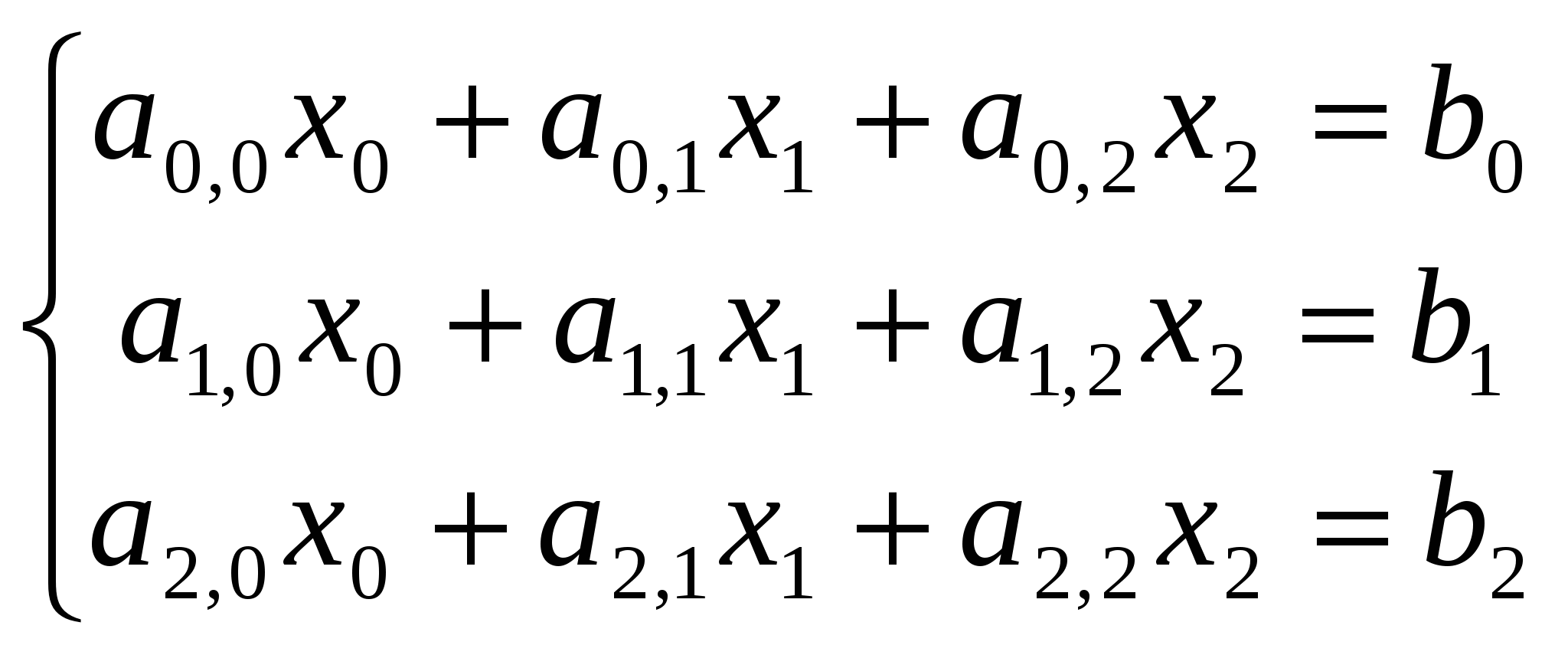 (7.1)
(7.1)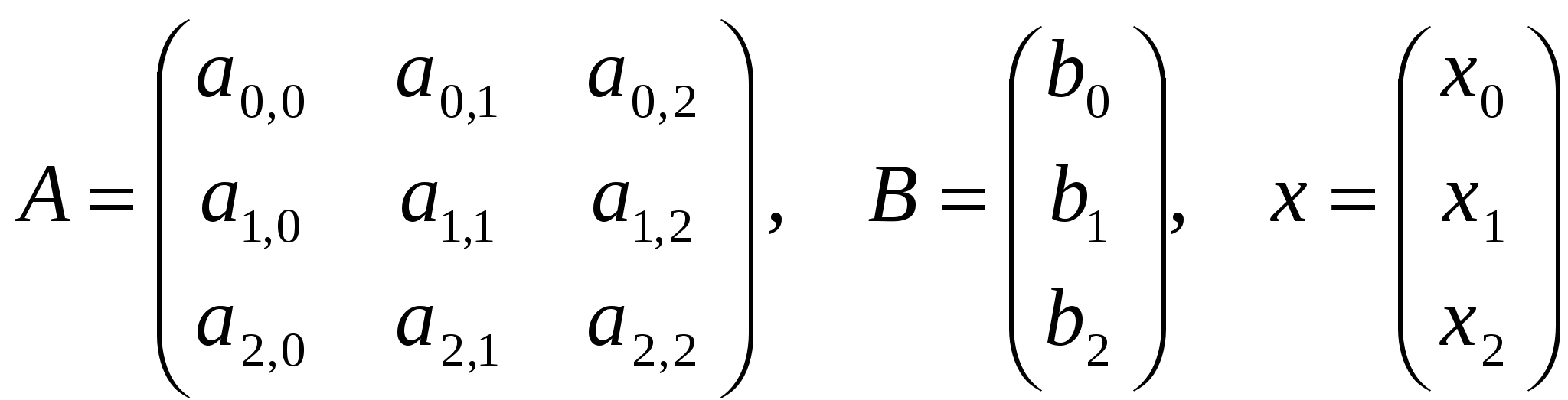 , (7.2)
, (7.2)