4. Основы расчета теории надежности. Основы теории расчета надежности технических систем
 Скачать 2.78 Mb. Скачать 2.78 Mb.
|
|
4. Резервирование Резервирование — метод повышения надежности объекта введением дополнительных элементов и функциональных возможностей сверх минимально необходимых для нормального выполнения объектом заданных функций. В этом случае отказ наступает только после отказа основного элемента и всех резервных элементов. Систему можно представить из ряда ступеней, выполняющих отдельные функции. Задача резервирования состоит в нахождении такого числа резервных образцов оборудования на каждой ступени, которое будет обеспечивать заданный уровень надежности системы при наименьшей стоимости. Выбор наилучшего варианта зависит главным образом от того увеличения надежности, которое можно достичь при заданных расходах. Основной элемент — элемент основной физической структуры объекта, минимально необходимой для нормального выполнения объектом его задач. Резервный элемент — элемент, предназначенный для обеспечения работоспособности объекта в случае отказа основного элемента. 4.1. Виды резервирования Структурное (элементное) резервирование — метод повышения надежности объекта, предусматривающий использование избыточных элементов, входящих в физическую структуру объекта. Обеспечивается подключением к основной аппаратуре резервной таким образом, чтобы при отказе основной аппаратуры резервная продолжала выполнять ее функции. Резервирование функциональное — метод повышения надежности объекта, предусматривающий использование способности элементов выполнять дополнительные функции вместо основных и наряду с ними. Временное резервирование — метод повышения надежности объекта, предусматривающий использование избыточного времени, выделенного для выполнения задач. Другими словами, временное резервирование — такое планирование работы системы, при котором создается резерв рабочего времени для выполнения заданных функций. Резервное время может быть использовано для повторения операции, либо для устранения неисправности объекта. Информационное резервирование — метод повышения надежности объекта, предусматривающий использование избыточной информации сверх минимально необходимой для выполнения задач. Нагрузочное резервирование — метод повышения надежности объекта, предусматривающий использование способности его элементов воспринимать дополнительные нагрузки сверх номинальных. С позиций расчета и обеспечения надежности технических систем необходимо рассматривать структурное резервирование. 4.2. Способы структурного резервирования По способу подключения резервных элементов и устройств различают следующие способы резервирования (рис. 4.4.1). 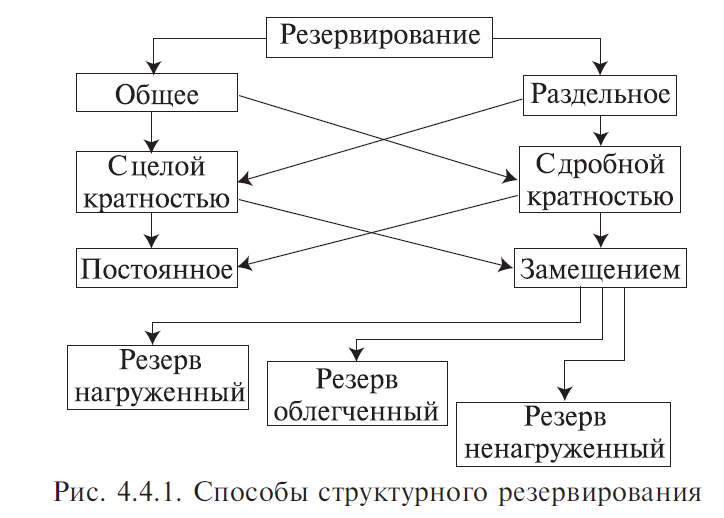 Резервирование раздельное (поэлементное) с постоянным включением резервных элементов (рис. 4.4.2). Такое резервирование возможно тогда, когда подключение резервного элемента несущественно изменяет рабочий режим устройства. Достоинство его — постоянная готовность резервного элемента, отсутствие затраты времени на переключение. Недостаток — резервный элемент расходует свой ресурс так же, как основной элемент. 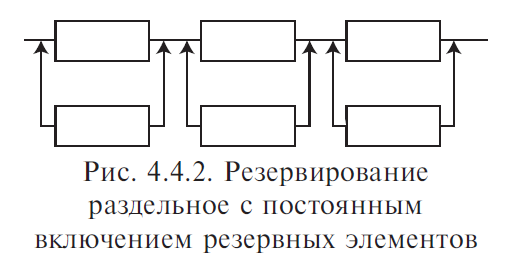 Резервирование раздельное с замещением отказавшего элемента одним резервным элементом (рис. 4.4.3). Это такой способ резервирования, при котором резервируются отдельные элементы объекта или их группы. В этом случае резервный элемент находится в разной степени готовности к замене основного элемента. Достоинство этого способа в том, что резервный элемент сохраняет свой рабочий ресурс, либо может быть использован для выполнения самостоятельной задачи. Рабочий режим основного устройства не искажается. Недостаток способа в том, что необходимость затрачивать время на подключение резервного элемента. Резервных элементов может быть меньше, чем основных. 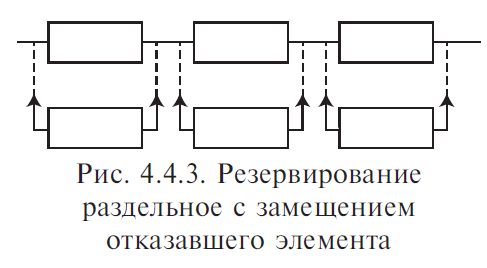 Отношение числа резервных элементов к числу резервируемых называется кратностью резервирования — m. При резервировании с целой кратностью величина m есть целое число, при резервировании с дробной кратностью величина m есть дробное несокращаемое число. Например, m = 4/2 означает наличие резервирования с дробной кратностью, при котором число резервных элементов равно четырем, число основных — двум, а общее число элементов равно шести. Сокращать дробь нельзя, так как если m = 4/2 = 2/1, то это означает, что имеет место резервирование с целой кратностью, при котором число резервных элементов равно двум, а общее число элементов равно трем. При включении резерва по способу замещения резервные элементы до момента включения в работу могут находиться в трех состояниях: — нагруженном резерве; — облегченном резерве; — ненагруженном резерве. Нагруженный резерв — резервный элемент, находящийся в том же режиме, что и основной. Облегченный резерв — резервный элемент, находящийся в менее нагруженном режиме, чем основной. Ненагруженный резерв — резервный элемент, практически не несущий нагрузок. Резервирование общее с постоянным подключением, либо с замещением (рис. 4.4.4). В этом случае резервируется объект в целом, а в качестве резервного — используется аналогичное сложное устройство. Этот способ менее экономен, чем раздельное резервирование. При отказе, например, первого основного элемента возникает необходимость подключать всю технологическую резервную цепочку. 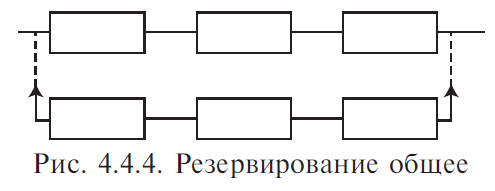 Резервирование мажоритарное («голосование» n из m элементов) (рис. 4.4.5). Этот способ основан на применении дополнительного элемента — его называют мажоритарный, или логический, или кворум-элемент. 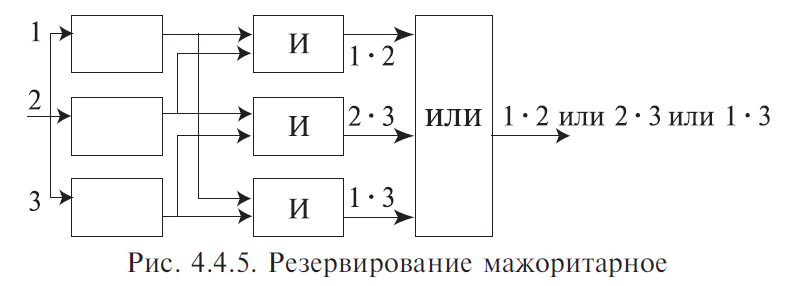 Он позволяет вести сравнение сигналов, поступающих от элементов, выполняющих одну и ту же функцию. Если результаты совпадают, тогда они передаются на выход устройства. На рис. 4.4.5 изображено резервирование по принципу голосования «два из трех», т. е. любые два совпадающих результата из трех считаются истинными и проходят на выход устройства. Можно применять соотношения три из пяти и др. Главное достоинство этого способа — обеспечение повышения надежности при любых видах отказов работающих элементов. Любой вид одиночного отказа элемента не окажет влияния на выходной результат. 4.5. Основы расчета надежности технических систем по надежности их элементов 4.5.1. Целевое назначение и классификация методов расчета Расчеты надежности — расчеты, предназначенные для определения количественных показателей надежности. Они проводятся на различных этапах разработки, создания и эксплуатации объектов. На этапе проектирования расчет надежности производится с целью прогнозирования (предсказания) ожидаемой надежности проектируемой системы. Такое прогнозирование необходимо для обоснования предполагаемого проекта, а также для решения организационно-технических вопросов: — выбора оптимального варианта структуры; — способа резервирования; — глубины и методов контроля; — количества запасных элементов; — периодичности профилактики. На этапе испытаний и эксплуатации расчеты надежности проводятся для оценки количественных показателей надежности. Такие расчеты носят, как правило, характер констатации. Результаты расчетов в этом случае показывают, какой надежностью обладали объекты, прошедшие испытания или используемые в некоторых условиях эксплуатации. На основании этих расчетов разрабатываются меры по повышению надежности, определяются слабые места объекта, даются оценки его надежности и влияния на нее отдельных факторов. Многочисленные цели расчетов привели к большому их разнообразию. На рис. 4.5.1 изображены основные виды расчетов. Элементный расчет — определение показателей надежности объекта, обусловленных надежностью его комплектующих частей (элементов). В результате такого расчета оценивается техническое состояние объекта (вероятность того, что объект будет находиться в работоспособном состоянии, средняя наработка на отказ и т. п.). Расчет функциональной надежности — определение показателей надежности выполнения заданных функций (например, вероятность того, что система очистки газа будет работать заданное время, в заданных режимах эксплуатации, с сохранением всех необходимых параметров по показателям очистки). Поскольку такие показатели зависят от ряда действующих факторов, то, как правило, расчет функциональной надежности более сложен, чем элементный расчет. Выбирая на рис 4.5.1 варианты перемещений по пути, указанному стрелками, каждый раз получаем новый вид (случай) расчета. 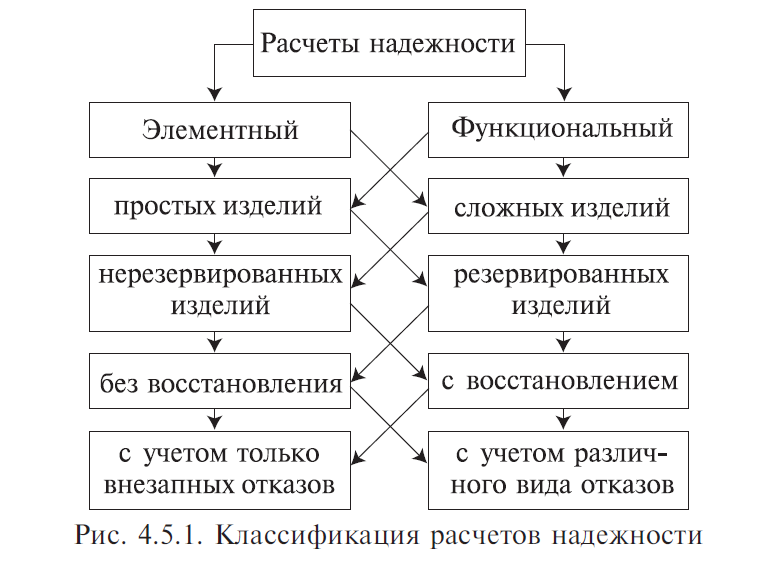 Самый простой расчет — расчет, характеристики которого представлены на рис. 4.5.1 слева: элементный расчет аппаратурной надежности простых изделий, нерезервированных, без учета восстановлений работоспособности при условии, что время работы до отказа подчинено экспоненциальному распределению. Самый сложный расчет — расчет, характеристики которого представлены на рис. 4.5.1 справа: функциональной надежности сложных резервированных систем с учетом восстановления их работоспособности и различных законов распределения времени работы и времени восстановления. Выбор того или иного вида расчета надежности определяется заданием на расчет надежности. На основании задания и последующего изучения работы устройства (по его техническому описанию) составляется алгоритм расчета надежности, т. е. последовательность этапов расчета и расчетные формулы. 4.5.2. Последовательность расчета систем Последовательность расчета системы представлена на рис. 4.5.2. Рассмотрим основные ее этапы. Прежде всего следует четко сформулировать задание на расчет надежности. В нем должны быть указаны: 1) назначение системы ее состав и основные сведения о функционировании; 2) показатели надежности и признаки отказов, целевое назначение расчетов; 3) условия, в которых работает (или будет работать) система; 4) требования к точности и достоверности расчетов, к полноте учета действующих факторов. На основании изучения задания делается вывод о характере предстоящих расчетов. В случае расчета функциональной надежности осуществляется переход к этапам 4-5-7, в случае расчета элементов (аппаратурной надежности) — к этапам 3-6-7. 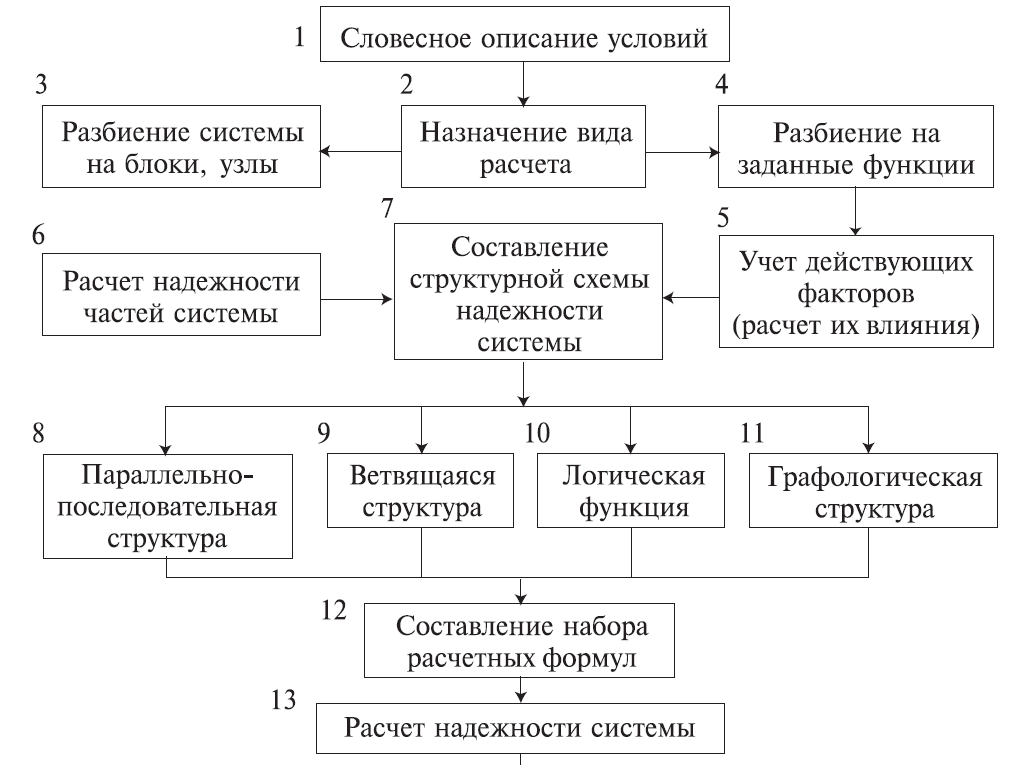  Под структурной схемой надежности понимается наглядное представление (графическое или в виде логических выражений) условий, при которых работает или не работает исследуемый объект (система, устройство, технический комплекс и т. д.). Типовые структурные схемы представлены на рис. 4.5.3. Простейшей формой структурной схемы надежности является параллельно-последовательная структура. На ней параллельно соединяются элементы, совместный отказ которых приводит к отказу объекта. В последовательную цепочку соединяются такие элементы, отказ любого из которых приводит к отказу объекта. На рис. 4.5.3, а представлен вариант параллельно-последовательной структуры. По этой структуре можно сделать следующее заключение. Объект состоит из пяти частей. Отказ объекта наступает тогда, когда откажет или элемент 5, или узел, состоящий из элементов 1—4. Узел может отказать тогда, когда одновременно откажет цепочка, состоящая из элементов 3, 4 и узел, состоящий из элементов 1, 2. Цепь 3—4 отказывает, если откажет хотя бы один из составляющих ее элементов, а узел 1, 2 — если откажут оба элемента, т. е. элементы 1, 2. Расчет надежности при наличии таких структур отличается наибольшей простотой и наглядностью. Однако не всегда удается условие работоспособности представить в виде простой параллельно- последовательной структуры. В таких случаях используют или логические функции, или графы и ветвящиеся структуры, по которым оставляются системы уравнений работоспособности. 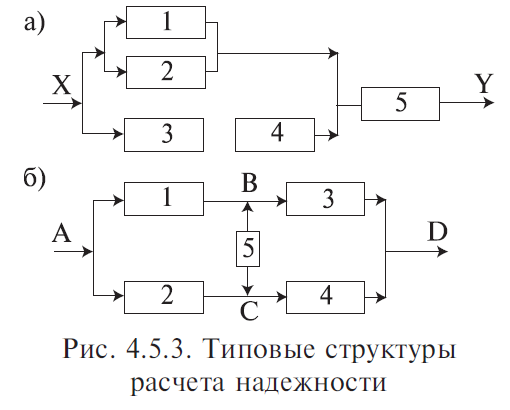 На основе структурной схемы надежности составляется набор расчетных формул. Для типовых случаев расчета используются формулы, приведенные в справочниках по расчетам надежности, стандартах и методических указаниях. Прежде чем применять эти формулы, необходимо предварительно изучить их существо и область использования. 4.5.3. Расчет надежности, основанный на использовании параллельно-последовательных структур Пусть некоторая техническая система D составлена из n элементов (узлов). Допустим, надежности элементов нам известны. Возникает вопрос об определении надежности системы. Она зависит от того, каким образом элементы объединены в систему, какова функция каждого из них и в какой мере исправная работа каждого элемента необходима для работы системы в целом. Параллельно-последовательная структура надежности сложного изделия дает представление о связи между надежностью изделия и надежностью его элементов. Расчет надежности ведется последовательно — начиная от расчета элементарных узлов структуры к ее все более сложным узлам. Например, в структуре (рис. 4.5.3, а) узел, состоящий из элементов 1—2 — элементарный узел, состоящий из элементов 1—2—3—4 — сложный. Эта структура может быть сведена к эквивалентной, состоящей из элементов 1—2—3—4 и элемента 5, соединенных последовательно. Расчет надежности в данном случае сводится к расчету отдельных участков схемы, состоящих из параллельно и последовательно соединенных элементов. 4.5.3.1. Система с последовательным соединением элементов Самым простым случаем в расчетном смысле является последовательное соединение элементов системы. В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен размыканию всей цепи, мы и называем такое соединение «последовательным» (рис. 4.5.4). 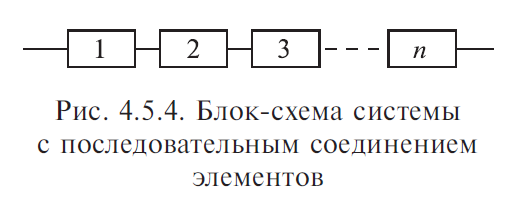 Следует пояснить, что «последовательным» такое соединение элементов является только в смысле надежности, физически они могут быть соединены как угодно. С позиции надежности такое соединение означает, что отказ устройства, состоящего из этих элементов, происходит при отказе элемента 1, или элемента 2, или элемента 3, или элемента n. Условие работоспособности можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1, и элемент 2, и элемент 3, и элемент n. Выразим надежность данной системы через надежности ее элементов. Пусть имеется некоторый промежуток времени (0,τ), в течение которого требуется обеспечить безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности Р(t), нам важно знать значение этой надежности при t = τ, т. е. Р(τ). Это не функция, а определенное число; отбросим аргумент τ и обозначим надежность системы просто Р. Аналогично обозначим надежности отдельных элементов P1, P2, P3, ..., Pn. Для безотказной работы простой системы в течение времени τ нужно, чтобы безотказно работал каждый из ее элементов. Обозначим S — событие, состоящее в безотказной работе системы за время ; s1, s2, s3, ..., sn — события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий s1, s2, s3, ..., sn: Предположим, что элементы s1, s2, s3, ..., sn отказывают независимо друг от друга (или, как говорят применительно к надежности, «независимы по отказам», а совсем кратко: «независимы»). Тогда по правилу умножения вероятностей для независимых событий P(S ) = P(s1 ) ⋅P(s2 ) ⋅P(s3 ) ⋅ ... ⋅P(sn ) или в других обозначениях: а короче:  т. е. надежность (вероятность работоспособного состояния) простой системы, составленной из независимых по отказам, последовательно соединенных элементов, равна произведению надежностей ее элементов. В частном случае, когда все элементы обладают одинаковой надежностью P1 = P2 = P3 = ... = Pn, выражение (4.5.2) принимает вид: ПРИМЕР 4.5.1. Система состоит из 10 независимых элементов, надежность каждого из которых равна Р =0,95. Определить надежность системы. По формуле (4.5.3) Р = 0,9510 ≈ 0,6. Из примера видно, как резко падает надежность системы при увеличении в ней числа элементов. Если число элементов n велико, то для обеспечения хотя бы приемлемой надежности Р системы каждый элемент должен обладать очень высокой надежностью. Поставим вопрос: какой надежностью Р должен обладать отдельный элемент для того, чтобы система, составленная из n таких элементов, обладала заданной надежностью Р ? Из формулы (4.5.3) получим: |
