конспект. Основная литература
 Скачать 1 Mb.
|
Значения N при =0,95 и различных p и
Из таблицы видно, что при увеличении точности (т.е. уменьшении ) существенно увеличивается необходимое число испытаний N. Это является одним из ограничений применимости данного метода. Его целесообразно применять для решения тех задач, где требования к точности не являются слишком жёсткими. На практике определение N затрудняется тем, что не всегда известно значение Р. Допустимо в целях оценки N вместо Р брать частоту  . Для этого выполняются следующие операции: 1) Сначала выбирается N=N0 (например для Р=0,1). 2) Затем, после N0 испытаний вычисляется и по формуле (9) уточняется значение N.3) Если NN0, то проводятся дополнительные испытания. В случае, когда после дополнительных испытаний происходит изменение , то уточнение значения N необходимо продолжить. Можно также пользоваться максимальным значением N при р=0,5. Пусть требуется вычислить интеграл:  (10)причём подынтегральная функция удовлетворяет условию 0g(x)1 (11) 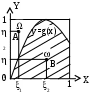 Будем рассматривать на плоскости две области: 1) 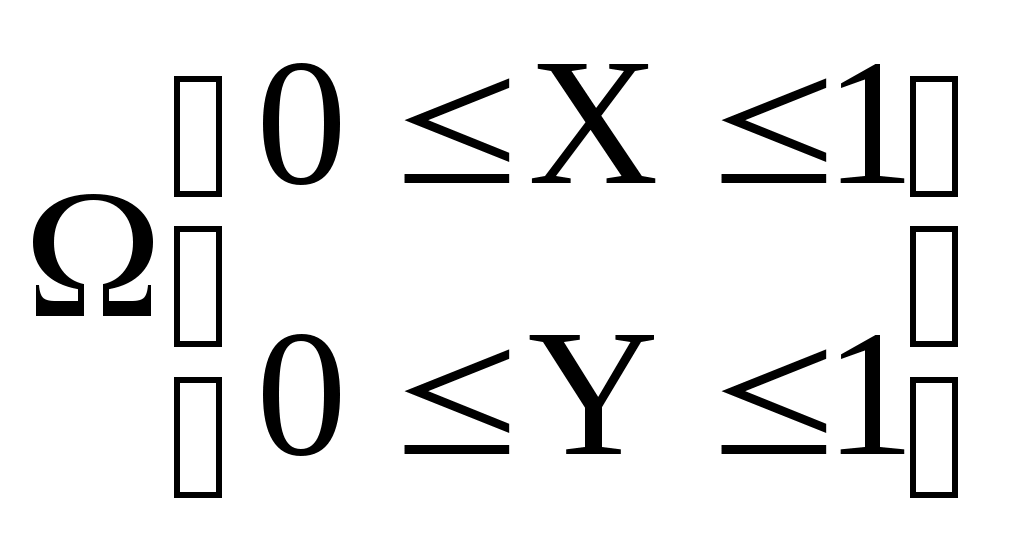 2) Область ограничена кривой y=g(x), осью ОХ и ординатами х=0; и х=1. Легко видеть, что величина интеграла I в точности равна площади S области , а площадь S=1. Зададим в области равномерное распределение случайной точки (,). Совместная функция плотности f(x,y) случайных величин и в области равна единице. Вероятность попадания точки (,) в область равна:  Проводим эксперимент по генерации значений координат точки (,): (Xi,Yi). Если появившаяся точка (Xi,Yi) принадлежит области , то испытание будем считать удачным. После проведения N испытаний подсчитаем число удачных испытаний и вычислим частоту  попадания случайной точки (,) в область : При N  .По данному алгоритму отметим два замечания: по получению координат Xi,Yi. Обычно имеется одномерная совокупность случайных чисел с равномерным распределением (0,1). Будем выбирать из этой совокупности пары последовательных чисел и будем считать их координатами Xi,Yi случайной точки. Точки с такими координатами будут иметь равномерное распределение в области ; по способу проверки факта попадания случайной точки в область . Для этого используется неравенство: yg(x) (13) Предположим теперь, что необходимо вычислить интеграл:  (14)в конечных пределах (a,b). Обозначим наибольшее и наименьшее значения h(x) на (a,b) соответственно M и L. Заменой переменных X=a+(b–a)Z и изменением масштаба по оси h(x) преобразуем интеграл (14) к виду:   Введём обозначения: (M–L)(b-a)=S L(b–a)=S0  Тогда: I=SI*+S0, где  Таким образом, мы свели вычисление интеграла (14) к случаю (10) (где  )В разделе 4-й этап построения модели – проведение эксперимента мы отмечали следущее. «Экспериментальное исследование состоит в том, по крайней мере, из трёх разделов. 1.Измерение. 2.Аналитическое описание. 3.Феноменологическое описание результатов.». Рассмотрим первый раздел более подробно. Классификация измерений Измерения являются средством получения информации о свойствах физических объектов, о закономерностях протекающих процессов и т.д. Измерение (согласно ГОСТ 16263-70) – это нахождение физической величины опытным путём с помощью специальных технических средств. Измерение – это операция, посредством которой определяется отношение измеряемой величины к другой однородной величине, принимаемой за единицу. Выражающая это отношение величина называется численным значением измеряемой величины. Различают три наиболее общих метода измерений: 1. Прямые. 2. Косвенные. 3. Совокупные. Эта классификация важна, т.к. каждая её категория связана с определённым способом обработки данных. Согласно ГОСТ 16263-70, совокупные измерения позже стали делить на собственно совокупные и совместные. При прямых измерениях объект исследования приводят во взаимодействие со средством измерений и по показаниям последнего отсчитывают значение измеряемой величины. Показания прибора могут умножаться на некоторый коэффициент, могут вводиться поправки и т.д. При косвенных измерениях искомое значение измеряемой величины находят на основании известной зависимости между этой величиной и величинами-аргументами. Аргументы находят прямыми или другими способами измерений. Например,  , где m и V измеряют непосредственно. Совместные и совокупные измерения по способам нахождения искомых значений измеряемых величин очень близки: в обоих случаях они находятся путём решения системы уравнений (обычно прямых). Отличие в том, что при совокупных измерениях одновременно измеряют несколько одноимённых величин, а при совместных – разноимённых. Пример совместных измерений: когда сопротивление резистора при t = 20C и его температурные коэффициенты находят по данным прямых измерений R и t, выполненных при разных температурах. А к совокупным, например, можно отнести измерения, при которых массы отдельных гирь набора находят по известной массе одной из них, и по результатам сравнения масс различных сочетаний гирь данного набора.Классификация погрешностей Анализ и оценивание погрешностей измерений – это один из разделов метрологии – науки об измерениях. Рассмотрим наиболее важные термины раздела: Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. По форме выражения различают абсолютные и относительные погрешности. Абсолютная погрешность – выражается в единицах измеряемой величины:  , где  – соответственно измеренное и истинное значения величины.Относительная погрешность выражается в процентах или в относительной доле измеряемой величины:  .Под точностью измерений понимается качество измерений, отражающее близость их результатов к истинному значению величины. Точность количественно можно охарактеризовать числом, равным обратному значению относительной погрешности. Например, если:  , то точность равна 5104. Различают также аддитивную и мультипликативную погрешности. Аддитивная погрешность не зависит от значения измеряемой величины. Её иногда называют погрешностью суммирования (от англ.) или погрешностью установки нуля. В этом случае результат измерения равен:  Мультипликативная погрешность пропорциональна значению измеряемой величины:  Обязательными компонентами всякого измерения являются: метод измерения, средства измерения и участие человека. Несовершенство каждого компонента вносит вклад в погрешность измерения:  ,где  – методическая погрешность;  – инструментальная погрешность;  – личная погрешность.Методические погрешности могут возникать из-за несовершенства теории тех явлений, которые положены в основу метода измерений (например, неточность соотношений, неточность (грубость) модели и т.д.). Инструментальные погрешности обусловлены несовершенством средств измерений (например, измерения в нормальных условиях и при отклонении от нормальных условий). Личные погрешности связаны с индивидуальными особенностями лица, выполняющего измерения. Усовершенствование конструкций средств измерений позволило свести личные погрешности к минимуму. Рассмотрим классификацию по свойствам погрешностей при повторных измерениях, согласно которой погрешности подразделяются на систематические и случайные. Систематической погрешностью измерения называется составляющая, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Для исключения (т.е. компенсации) постоянной систематической погрешности применяются следующие методы. Введение поправки, равной по абсолютному значению и противоположной по знаку систематической погрешности. Метод замещения, представляющий собой разновидность метода сравнения, когда сравнение осуществляется путём замены измеряемой величины известной (т.е. образцовой) величиной. В этом случае значение измеряемой величины равно известному значению меры, а средства измерения используются фактически для их сравнения. Метод компенсации погрешности по знаку, предусматривающий два измерения, выполняемые так, чтобы постоянная систематическая погрешность в результат каждого из них входила с разными знаками. Если вычислить результат как среднее арифметическое, то погрешность компенсируется. Мы рассмотрели систематическую погрешность. Случайной погрешностью называется погрешность измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Здесь обработка результатов измерений выполняется на основе методов теории вероятности и мат. статистики. Рассмотрим, как уменьшить погрешность измерений аппаратурными методами. Аппаратурные методы повышения точности измерений Один из методов повышения точности измерений (т.е. уменьшения погрешности) – это конструктивно-технологический, основанный на выявлении причин и источников наиболее существенных погрешностей и всемерном снижении их влияния. Однако возможности этого метода весьма ограничены. И кроме того, его применение с целью достижения высокой точности приводит к резкому возрастанию стоимости средств измерений. Поэтому широкое распространение получили методы повышения точности, основанные на введении структурной и (или) временной избыточности, т.е. на введении дополнительных средств измерений (а именно – измерительных преобразователей) и (или) выполнении дополнительных измерений, результаты которых обрабатываются по специальному алгоритму, позволяющему повысить точность. Примеры: 1) Метод отрицательной обратной связи: 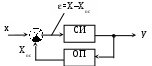 где СИ – система измерений; ОП – обратный преобразователь. Данный метод следует применять, когда погрешности ОП погрешностей СИ; 2) Метод вспомогательных измерений. Он основан на том, что если имеют место легко учитываемые дестабилизирующие факторы, то погрешности от них, вычисленные вычислительным устройством, добавляются (или вычитаются) к измеренной величине. 3) Итерационные методы. Их особенность в том, что в процессе коррекции результат уточняется в несколько раз, т.е. находится методом последовательных приближений. 4) Методы образцовых мер. Они основаны на определении в процессе цикла измерений реальных значений параметров функций преобразования СИ путём отключения от входа СИ измеряемой величины и подключения образцовых мер. Недостатком метода является периодическое переключение входа и большое число образцовых измерений, если нелинейность функции преобразования существенна. 5) Тестовые методы. Их сущность в том, что в процессе цикла измерений получают информацию не только о значении измеряемой величины, но и о параметрах функции преобразования СИ в момент измерения. В отличие от метода образцовых мер используются тесты, формируемые с участием измеряемой величины. И это позволяет не отключать измеряемую величину от входа СИ. На практике часто приходится решать задачу о назначении допусков на измеряемые переменные по заданному допуску на выходную величину, и наоборот. Рассмотрим 5-й этап построения модели. ОБРАБОТКА И АНАЛИЗ РЕЗУЛЬТАТОВ Постановка задачи обработки | ||||||||||||||||||||||||||||||||||||||||