конспект. Основная литература
 Скачать 1 Mb.
|
|
Полиномы, проходящие через заданные точки На практике встречаются следующие задачи. Производится n измерений в каждой точке зависимости y=f(x). Затем в каждой точке находится среднее значение и средняя квадратическая погрешность. Далее решается задача подбора зависимости y=f(x), проходящей через все полученные точки. Поскольку полиномы легко интегрируются и дифференцируются, такие многочленные модели находят широкое применение при небольшом числе экспериментальных точек. Так через данные две точки (х1,у1) и (х2,у2) можно провести только одну линию у=а0+а1х. Параметры этой прямой а0 и а1 определяются системой уравнений: 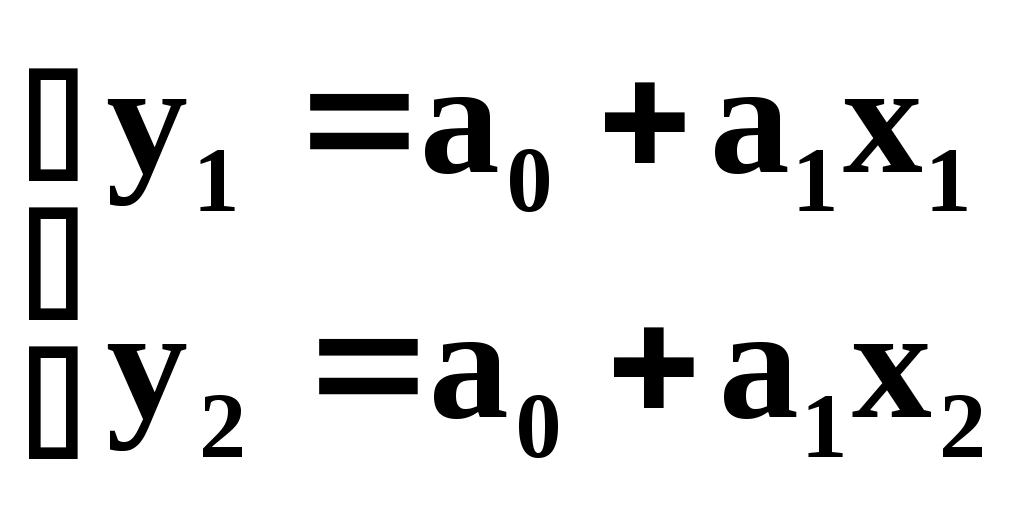 Подобным образом, через три различные точки можно провести только одну кривую не более чем второго порядка: у=а0+а1х+а2х2. Параметры а0,а1,а2 этой кривой определяются системой уравнений: 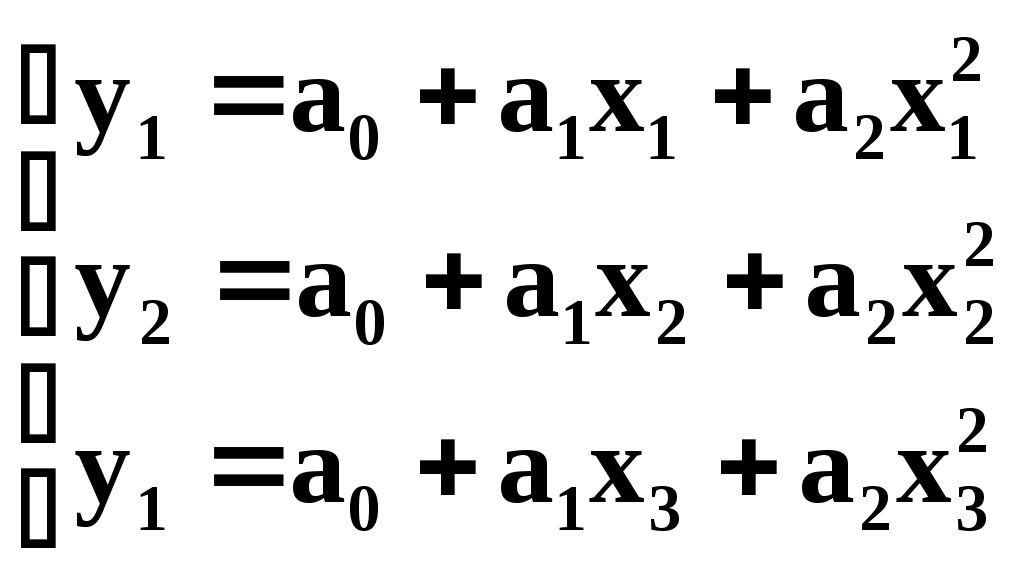 Для восьми экспериментальных точек в качестве эмпирической модели используется полином седьмой степени. Поскольку данный полином проходит через каждую из заданных точек, то результирующая сумма отклонений равна нулю. Недостатками применения полиномов в построении эмпирических моделей являются: 1) чувствительность коэффициентов аi к малым изменениям в исходных данных. 2) очень сильные колебания значений полинома на концах заданного интервала. При большом количестве экспериментальных данных используют сглаживающий полином более низкого порядка, полученный, например, по МНК. 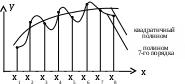 Для решения вопроса о порядке полинома для модели рассмотрим производные, например, полинома второго порядка у=а+bх+cх2;  ;  ;  . Таким образом, используя значения относительных разностей набора экспериментальных данных, по разностной таблице можно судить о поведении производных полинома для определения его порядка. Эмпирические модели на основе кубических сплайнов Использование какого-либо одного полинома для построения эмпирической модели не всегда приводит к надёжному соответствию расчётных и опытных данных. Наиболее эффективным в этом плане, хотя и более трудоёмким, является интерполяция функций методом кубических сплайнов. В этом методе используются различные кубические полиномы для каждой пары близлежащих экспериментальных точек. Рассмотрим интерполяцию кривой, проходящей через три экспериментальные точки с помощью двух кубических полиномов S1 и S2, которые задаются различными уравнениями  ,если х1хх2 и  если х2хх3 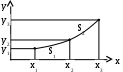 На этом графике экспериментальные точки 1,2,3 получены в результате отбрасывания промахов и последующего усреднения результатов в каждой точке (обычно по 30 измерениям). Для определения восьми коэффициентов полиномов a1,b1,…,c2,d2 необходимо иметь, естественно восемь уравнений. Их получение начнём с требований прохождения сплайна S1 через точки (х1,у1) и (х2,у2), а сплайна S2 – через точки (х2,у2) и (х3,у3). Это приводит к четырём уравнениям:     Наложим требование на гладкость кривой использованных сплайнов, т.е. равенства их первых производных в точке сопряжения (х2,у2). Это требование выразится пятым уравнением:  Требование равенства кривизны сплайна в этой же точке даёт шестое уравнение между искомыми коэффициентами:  Для нахождения двух оставшихся уравнений могут быть использованы два различных требования. Если представить общую кривую, составленную из двух сплайнов, в виде металлической линейки (т.е. гибкого стержня), закрепленной в точках х1, х2, х3, то концы линейки в крайних точках могут быть свободными или зафиксированными в определённом направлении. В первом случае говорят о нормальном сплайне, а во втором о фиксированном. Математическим условием нормального сплайна со свободными концами является постоянство первой производной, а значит – нулевое значение второй производной на крайних точках интервала (т.е. это, например, постоянный угол наклона из ствола):   Таким образом, мы получили систему из восьми алгебраических уравнений для определения восьми коэффициентов нормального сплайна. В случае фиксированного сплайна на его концах должны быть заданы значения первых производных, из чего можно вывести седьмое и восьмое уравнения:   ,где  – известные значения первых производных крайних сплайнов. Если продолжить аналогию с металлической линейкой, то данные значения определяют углы концов линейки по отношению к координатным осям Обычно, если информация о значениях первых производных на краевых точках отсутствует, то для аппроксимации расчётной кривой используются нормальные сплайны. Построение кубических сплайнов для большего числа экспериментальных точек осуществляется, обычно, с помощью операции сдвига. Данная процедура ввиду большого объёма вычислений требует для своей реализации специального алгоритма и вычислительной программы. Графическое представление результатов эксперимента Наибольшее распространение в графическом представлении результатов эксперимента получила линейная зависимость у=(х), поскольку зрительно мы можем идентифицировать только прямую линию. Рассмотрим практику эмпирического метода в виде развернутого плана. Линеаризация графика осуществляется на основе выбора одного из членов степенной последовательности. Здесь степень полинома равна единице. Для подгонки параметров а и b модели могут использоваться: сумма абсолютных отклонений, наибольшее абсолютное отклонение или сумма квадратов отклонений. Если адекватность такой модели экспериментальным данным не удовлетворяет, то переходят к составлению разностной таблицы и построению полиномной модели более высокого порядка. При небольшом числе n экспериментальных точек целесообразно попытаться подобрать полином порядка (n–1), проходящий через все n точки. В этом случае необходимо убедиться в отсутствии значительных осцилляций полинома на его конечных значениях. Если имеется значительное количество экспериментальных данных, то имеет смысл использовать полином низкого порядка, сглаживающий полученную зависимость. Для определения порядка сглаживающего полинома используется разностная таблица. В случае неадекватности сглаживающего полинома построение эмпирической модели осуществляется на основе кубических сплайнов. Теперь подробнее. Линейная модель Линейная зависимость очень широко распространена в графическом представлении экспериментальных данных, ввиду способности глаза выделять прямую линию из всего многообразия существующих линий. Даже если зависимость у=(х) нелинейная, графики стараются строить так, чтобы получить прямую линию. Например, если изучаемая зависимость имеет вид у=а+b/х2, то на графике строят зависимость у от 1/х2. В общем случае такие преобразования выполняют с использованием степенной последовательности  Например, формула Фаулера-Нордгейма для плотности тока автоэлектронной эмиссии имеет вид:  ; (1)Перепишем его в следующем виде:  или  где j [А/см2] – плотность тока; E=U/Z [В/см] – напряжённость поля; [эВ] – работа выхода электрона. Видно, что в координатах  функция (1) является прямой линией. Это позволяет находить (или Е) автоэмиссионным методом по тангенсу угла наклона прямой: Прямую проводят, используя экспериментальные данные. Далее проводится проверка (или другими словами) верификация модели на основе вычислений относительных отклонений расчётных и опытных данных. Рассмотрим 6-й этап построения моделей ПРОВЕРКА СПРАВЕДЛИВОСТИ ГИПОТЕЗ Для детерминированной модели обычно выполняется проверка справедливости гипотез двух видов. 1. Проверка физического смысла. 2. Математическая проверка. При проверке физического смысла устанавливается соответствие полученных результатов уже известным и определяется их практическая реальность. Мат. проверка может осуществляться через ответы на следующие основные вопросы. Их четыре. 1. Даёт ли уравнение имеющие смысл результаты, если его различные параметры устремлять к некоторому пределу Например, к нулю, к бесконечности или некоторому граничному значению. 2. Если одна величина изменяется, то ведут ли себя остальные величины так, как это ожидалось 3. Существуют ли другие немаловажные причины, которые не входят в уравнение 4. Все ли значимые факторы рассмотрены Далее проводятся тестовые испытания детерминированной модели на соответствие её экспериментальным данным. Следует помнить, что результаты, полученные при решении уравнений детерминированной модели справедливы только в рамках гипотез и допущений, принятых при построении модели. В случае соответствия детерминированной модели критерию практики и физическому смыслу принимается решение о пригодности к использованию созданной модели. В противном случае необходимо возвратиться к этапу «Выдвижение гипотез» и начать модернизацию детерминированной модели или созданию новой. В случае вероятностной модели производится проверка статистических гипотез. Задача проверки гипотез состоит в том, чтобы установить – противоречит выдвинутая гипотеза экспериментальным данным или нет. Алгоритм, в соответствии с которым экспериментальным данным ставится в соответствие решение – принять или отвергнуть гипотезу, называется решающим правилом. Дадим ещё определение. Статистической проверкой гипотез называется предположение относительно параметров или формы распределения генеральной совокупности, проверяемое на основе данных выборочного наблюдения. Статистическая гипотеза может относиться либо к законам распределения, либо к отдельным параметрам распределения. Идентификация закона распределения проводится для проверки совместимости экспериментальных данных с некоторым теоретическим распределением. Примерами статистических гипотез могут служить предположения, что размер изделий подчинён закону нормального распределения, или средняя работа выхода одного материала превышает среднюю работу выхода другого материала. Т.е. примерами статистических гипотез могут служить четыре следующие. 1. Нормальное распределение имеет заданные среднее и дисперсию. 2. Нормальное распределение имеет заданное среднее (о дисперсии ничего не говорится). 3. Распределение нормально (с каким-нибудь средним и дисперсией) 4. Два неизвестных непрерывных распределения одинаковы. Статистическая проверка гипотез Мир познаваем, но предела познанию нет. То, что не познано, то, что мы не можем учесть (т.е наблюдать, измерить) при рассмотрении нами конкретного явления, мы списываем за счёт явлений случайных, происходящих в опытах с определённой вероятностью, или принимающих конкретные значения из возможного ряда (т.е. допустимых) значений. Мы уже отмечали, что случайная величина Х полностью описывается интегральным законом (т.е. плотностью распределения). На практике часто используются более бедные характеристики, например, числовые, а именно: мат. ожидание, дисперсия и другие. Несмещёнными оценками с минимальной дисперсией этих числовых характеристик являются выборочное среднее  и выборочная дисперсия   (1)Часто рассеивание связано с качеством продукции. Например, рассеивание величины сопротивления резисторов определяет класс их точности. Определение класса точности резисторов по рассеиванию, оцененному по выборке ограниченного объёма это пример задачи статистической проверки гипотез при допусковом контроле качества продукции. Обозначим через 0 параметр рассеивания годной продукции и через 1 – негодной. Их отношение =1/0 называют расстоянием между конкурирующими гипотезами (т.е. между гипотезой Н0: т.е. =0 и альтернативной гипотезой Н1: т.е. =1). Последовательность проверки гипотезы следующая. Берётся независимая выборка х1,…,хn и по ней находится оценка ( х1,…,хn), например х2 по уравнению (1). Задается критическое значение кр, соответствующее заданному уровню значимости (т.е. риску поставщика) и определяющее критическую область проверки гипотезы Н0: кр=, где – точка оперативной характеристики: ()=1–F(). Если выборочная точка попадает в критическую область, то отвергаем гипотезу Н0 и принимаем альтернативную гипотезу Н1. Имеем:  (2)Определим риск заказчика:  (3)Если плотности распределения подобны, то:  (4)где =/1– (5) Риск поставщика (т.е. уровень значимости, или вероятность ошибки I-го рода) – это вероятность забраковать годную продукцию. Риск заказчика (т.е. вероятность ошибки II-го рода) – это вероятность принять негодную продукцию. Для пояснения вышесказанного сделаем рис: 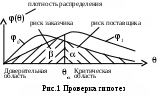 На данном рис. вероятности , соответствуют заштрихованным площадям под плотностями распределения. Видно противоречие между рисками. Чтобы уменьшить риск поставщика , нужно сместить границу критической области вправо, но при этом возрастёт риск заказчика . Чем больше расстояние между конкурирующими гипотезами , тем больше разнесены друг от друга на рис.1 кривые 0() и 1(). Соответственно обеспечиваются меньшие риски поставщика и заказчика. Следовательно, чем меньше и при фиксированном , тем лучше, эффективнее оценка. Или чем меньше при фиксированных и , тем лучше оценка, или гипотезы более различимы. В случае точечного оценивания (например, номинальной величины сопротивления в парии резисторов) оценка тем лучше (т.е. эффективнее), чем меньше её дисперсия. Таким образом, логично использовать оценку, которая даёт: 1) ()=min; или 2) ()=min. Такую оценку назовём оптимальной в первом или втором смысле (т.е. по дисперсии или по расстоянию). Переход к оптимальным оценкам по критериям минимума дисперсии или расстояния между конкурирующими гипотезами – позволяет уменьшить объём выборок или повысить достоверность и точность оценок и контроля при фиксированном объёме выборок. А эффективность оценок – это предмет теории вероятностей и мат. статистики. |