конспект. Основная литература
 Скачать 1 Mb.
|
|
Обработка результатов совместных измерений При совместных измерениях искомые значения величин находят решением системы уравнений, связывающей эти величины с непосредственно измеряемыми. Предположим, что искомые значения величин определяются в результате решения системы линейных уравнений: 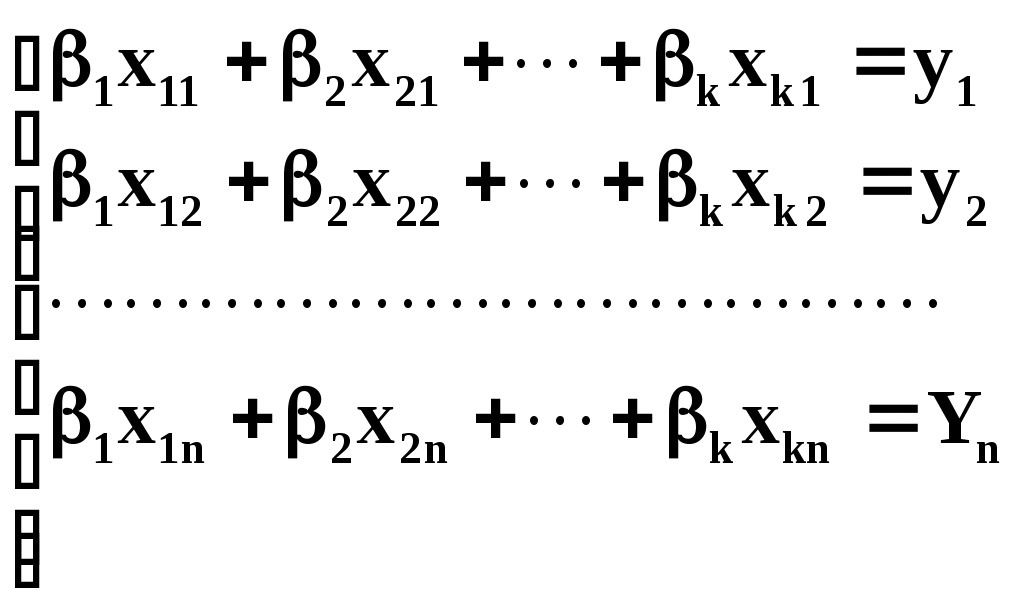 где i (при i=1,…,k) – искомые значения величин; yi (при j=1,…,n) – измеряемые значения величин; xi,j –известные величины. Эту систему уравнений можно переписать в виде: 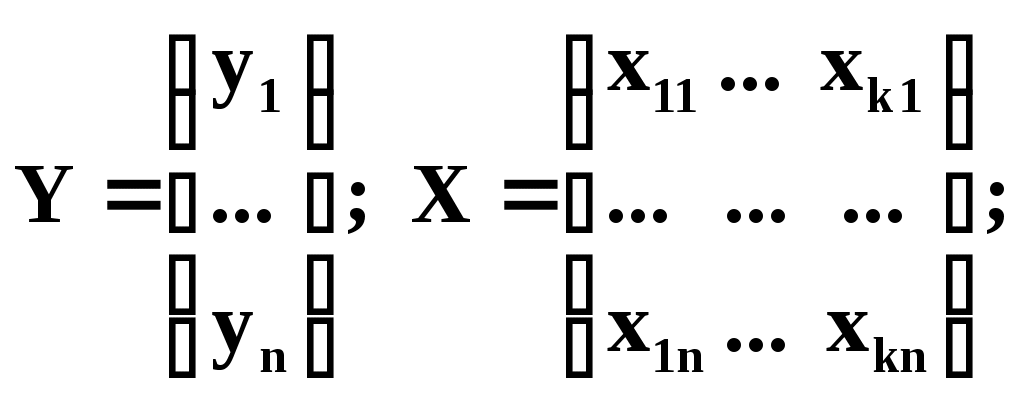 при (при j=1,…,n). Введём матричные обозначения:  Здесь Y,X – матрицы наблюдений; В – матрица неизвестных (искомых) постоянных величин; Е – матрица ошибок измерений Y. С учётом ошибок измерений модель, представленную в виде исходной системы уравнений, запишем как: Y=XB+E (4) Будем полагать, что матрица X не содержит линейно связанных столбцов и имеет ранг rg(X)=k. Если число уравнений n меньше числа неизвестных k, то rg(X)k и система (4) не имеет единственного решения. rg(X)=k, если Х не содержит линейно связанных столбцов и nk. В случае n=k система имеет единственное решение [это согласно Анго А. Математика для электро- и радиоинженеров.– М.: Наука, 1966, 779с.] В случае nk она, вообще говоря, не имеет решения, т.к. из-за ошибок наблюдения Е, которых мы не знаем, система оказывается несовместной. В этом случае система (4) называется условной. Решение ищется методами регрессионного анализа, например, по методу максимального правдоподобия. Эти методы мы рассмотрим отдельно. Рассмотрим методы обработки результатов измерений, связанные со статистическими погрешностями. Общая схема эмпирического построения модели Процедура построения вероятностной модели начинается с тщательного анализа исходных опытных данных, который преследует две цели: 1) исключить ошибочные данные и 2) установить эмпирическое соотношение между выбранными величинами. Для исключения ошибочных данных необходимо оценить величину ошибки. Если она превышает допустимые значения, следует провести дополнительные измерения, на основе которых можно отбросить ошибочный результат или заменить его на новый. Измерения следует продолжать до тех пор, пока результаты приобретут какой-то смысл, позволяющий установить наличие или отсутствие какого-либо соотношения, тренда между исследуемыми величинами. В экспериментах часто измеряются пары величин х и у, причём одна из них, у, является функцией другой, х. Затем найденные значения откладывают на графике и пытаются найти кривую, соответствующую алгебраической функции у=(х), которая проходила бы как можно ближе к экспериментальным точкам. Задача нахождения параметров функции (х) и составляет суть эмпирического метода моделирования. Метод наименьших квадратов (МНК) МНК применяется, когда из-за наличия случайных ошибок измерений (как говорят, из-за наличия «шума» в эксперименте) становится неразумным подбор формулы, описывающей все опытные значения. Т.е. когда при обработке опытных данных возникает задача о сглаживании экспериментальных зависимостей. При этом вид сглаживающей формулы должен быть известен заранее либо из теоретических соображений, либо из-за простоты аналитического представления. Пусть исследуется зависимость y=(x). Требуется определить вид этой зависимости. В результате опыта мы получаем ряд экспериментальных точек и строим график. 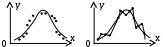 Случайные отклонения от видимой общей закономерности связаны с некоторыми ошибками измерения. Возникает вопрос: как наилучшим образом воспроизвести зависимость у от х Для решения подобных задач обычно применяется расчётный метод, известный под названием «МНК». Этот метод даёт возможность при заданном типе зависимости у=(х) так выбрать её числовые параметры, чтобы кривая у=(х) в известном смысле наилучшим образом отображала экспериментальные данные. Из каких соображений выбирается тип кривой у=(х) Часто этот вопрос решается непосредственно по внешнему виду экспериментальной зависимости. Н 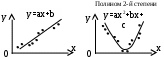 апример:Для периодической функции – это гармоники тригонометрического ряда. Часто также бывает, что вид зависимости (линейная, квадратическая, показательная) бывает известен из физических соображений, связанных с существом решаемой задачи. А из опыта требуется установить только некоторые параметры этой зависимости. Пусть имеются результаты n независимых опытов.
Из теоретических или иных соображений выбран вид зависимости у=(х). Функция у=(х) содержит ряд числовых параметров a,b,c,… Требуется так выбрать эти параметры, чтобы кривая у=(х) наилучшим образом изображала зависимость, полученную в опыте. Решение этой задачи зависит от того, что считать «наилучшим». Можно, например, наилучшим считать такое взаимное расположение точек кривой, при котором максимальное расстояние между ними обращается в минимум. А можно считать решение наилучшим, если сумма отклонений точек от кривой равна минимуму. В «МНК» сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращается в минимум. Преимущества «МНК»: 1) это сравнительно простой метод нахождения параметров кривой a,b,c,… 2) метод имеет довольно веское теоретическое обоснование с вероятностной точки зрения. Изложим это обоснование. Предположим, что истинная зависимость у от х выражается формулой у=(х). Экспериментальные точки уклоняются от этой зависимости вследствие ошибок измерения. Ошибки измерения, как правило, подчиняются нормальному закону. Рассмотрим какое-нибудь значение аргумента хi. Результат опыта есть случайная величина Yi, распределённая по нормальному закону с мат. ожиданием ( хi) и с СКО i, характеризующим ошибку измерения. Предположим, что точность измерения во всех точках одинакова: 1=2=…=n=. Тогда нормальный закон, которому подчиняется величина Yi, можно записать в виде: 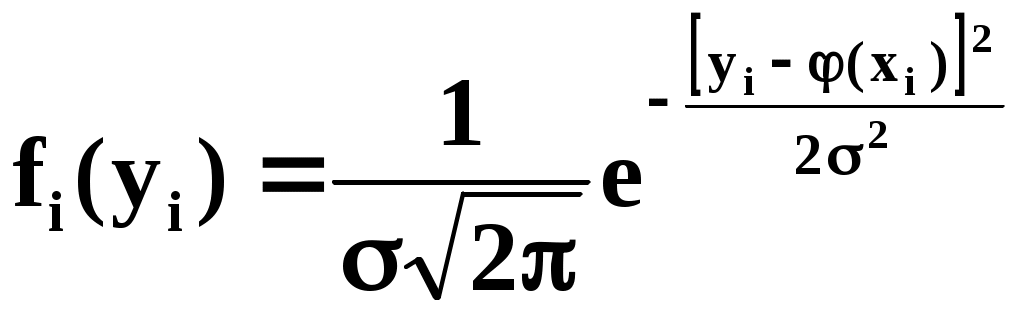 В результате нашего опыта (т.е. ряда измерений) произошло следующее событие: случайные величины (Y1,Y2,…,Yn) приняли совокупность значений (у1,у2,…,уn). Поставим задачу: так подобрать мат. ожидания (х1),(х2),…, (хn) чтобы вероятность этого события была максимальна (т.е. принцип максимального правдоподобия). Так как величины Yi непрерывны, то вероятность Yi=уi равна нулю. Поэтому будем пользоваться не вероятностями событий Yi=уi, а соответствующими элементами вероятностей: 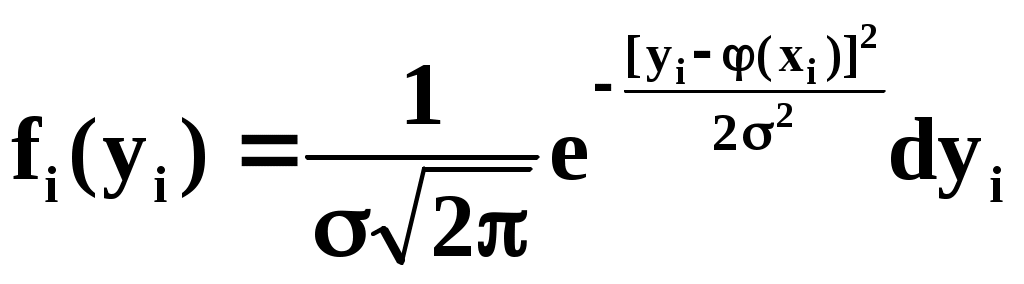 (1)Найдём вероятность того, что система случайных величин Y1,Y2,…,Yn примет совокупность значений, лежащих в пределах: (уi,уi+dуi), где i=1,2,…n. Так как опыты независимы, эта вероятность равна произведению элементов вероятностей (1) для всех значений i: 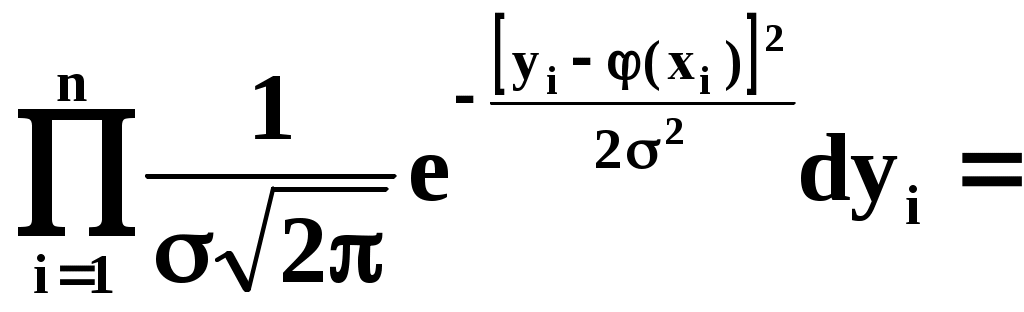  , (2)где k – коэффициент, не зависящий от (хi). Требуется так выбрать мат. ожидания (х1),(х2),…, (хn), чтобы (2) обращалась в максимум. Величина  – всегда меньше 1. Очевидно, она имеет наибольшее значение, когда показатель степени (по абсолютной величине) минимален: Отсюда, отбрасывая постоянный множитель 1/(2), получаем требование метода наименьших квадратов: Для того, чтобы данная совокупность наблюдённых значений у1,у2,…,уn была наивероятнейшей, нужно выбрать функцию (х) так, чтобы сумма квадратов отклонений наблюдённых значений уi от (хi) была минимальной:  Таким образом обосновывается МНК, исходя из нормального закона ошибок измерения и требования максимальной вероятности данной совокупности ошибок. Перейдём к задаче определения параметров a,b,c,… Функция у=(х) содержит параметры a,b,c,…, т.е. можно записать: у=(x,a,b,c,…). Требуется выбрать a,b,c,… исходя из условия:  (3)Найдём значения a,b,c,…, обращающие левую часть (3) в минимум. Для этого продифференцируем её по a,b,c,… и приравняем произведение нулю:  где  – значение частной производной функции по параметру а в точке xi.  – аналогично. Система содержит столько же уравнений, сколько параметров a,b,c,… Решить эту систему в общем виде нельзя, необходимо задаться конкретным видом функции . Рассмотрим два случая, наиболее часто встречающихся на практике: 1) когда – линейна; 2) когда – выражается полиномом второй степени (т.е.параболой). Рассмотрим первый случай. Подбор параметров линейной функции методом МНК 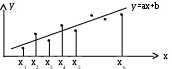 Требуется подобрать по МНК коэффициенты a и b линейной функции y=ax+b. Дифференцируем по a и b:   Подставляем производные в систему: 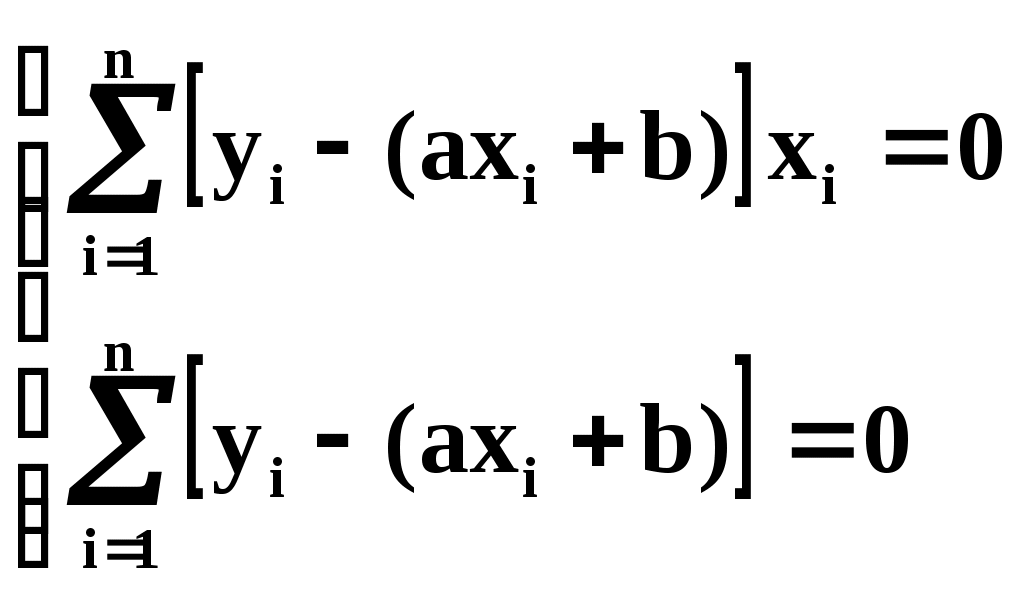 или раскрывая скобки и производя суммирование: 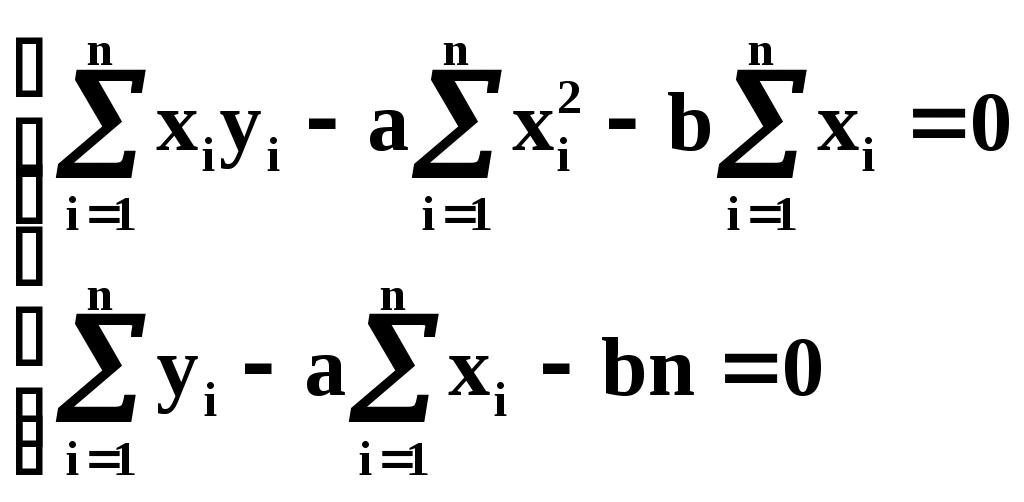 Разделим оба последних уравнения на n: 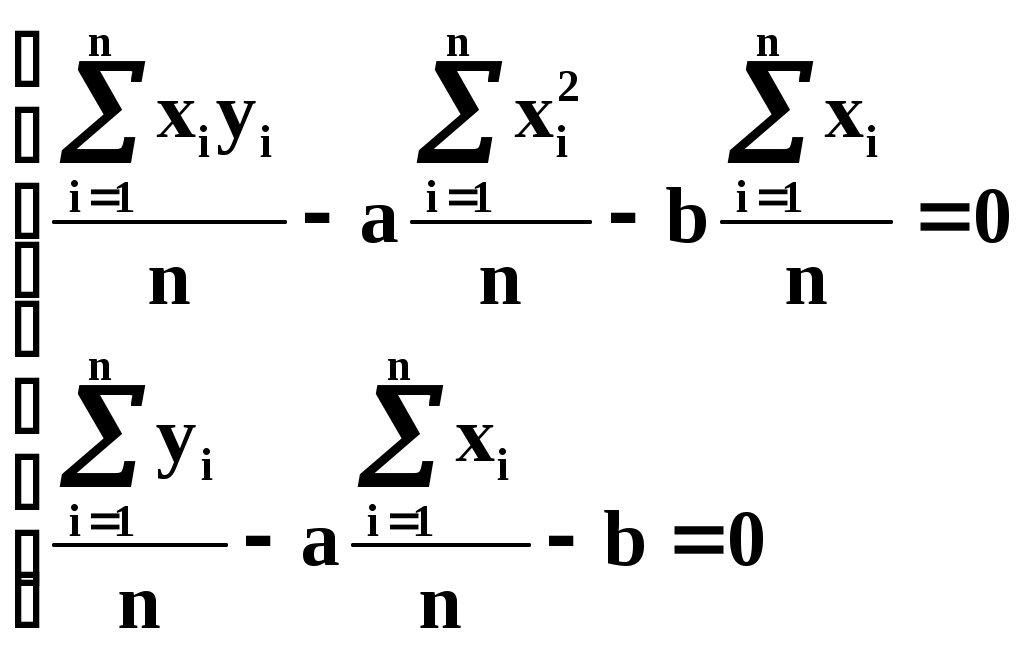 (4)Суммы представляют собой статистические моменты. Обозначим их: 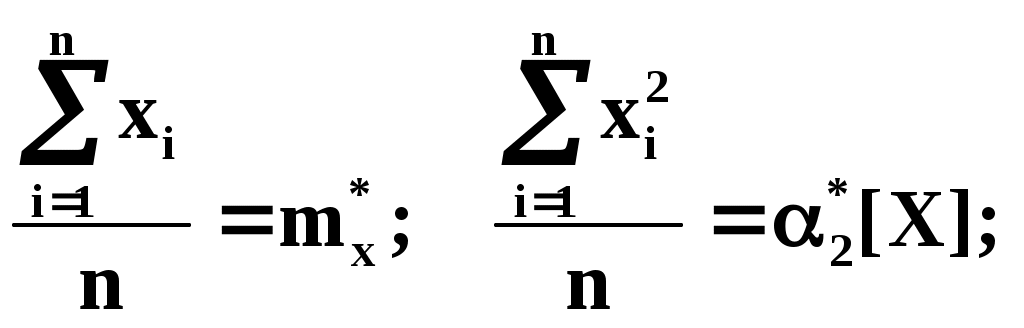 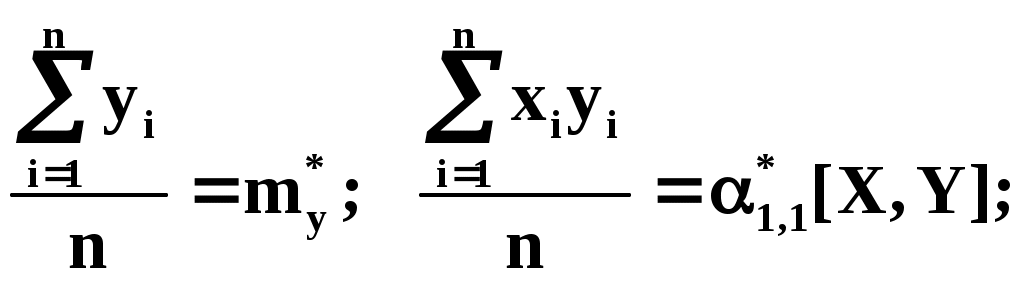 Подставляя в (4) эти выражения получаем: 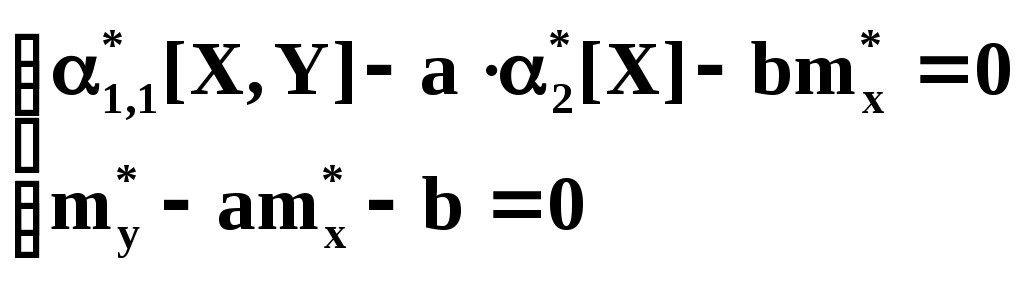 Выразим b из второго уравнения и подставим в первое:  Решая последнее уравнение относительно а, имеем:  Упростим выражение, введя не начальные, а центральные моменты: (это доказано в книгах, неинтересно):  откуда:  где 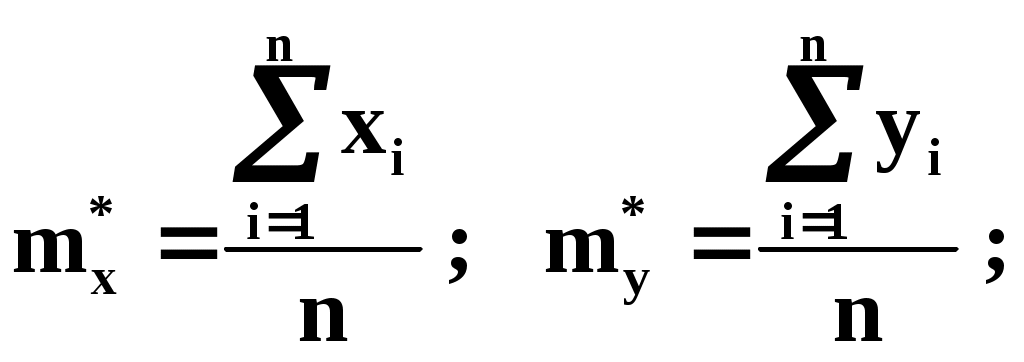 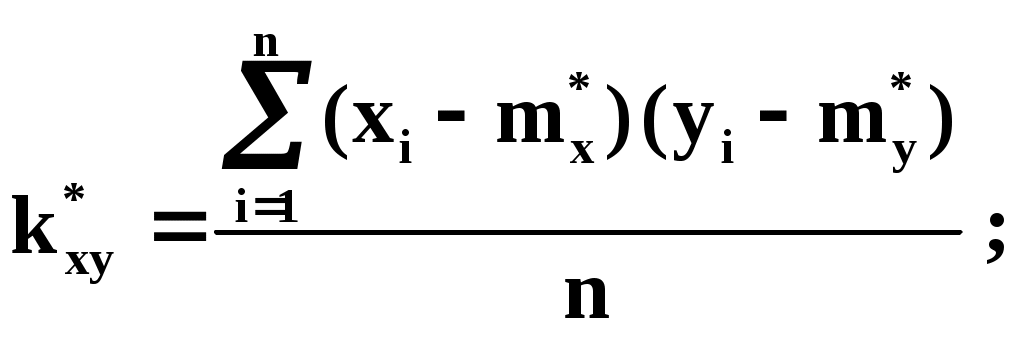 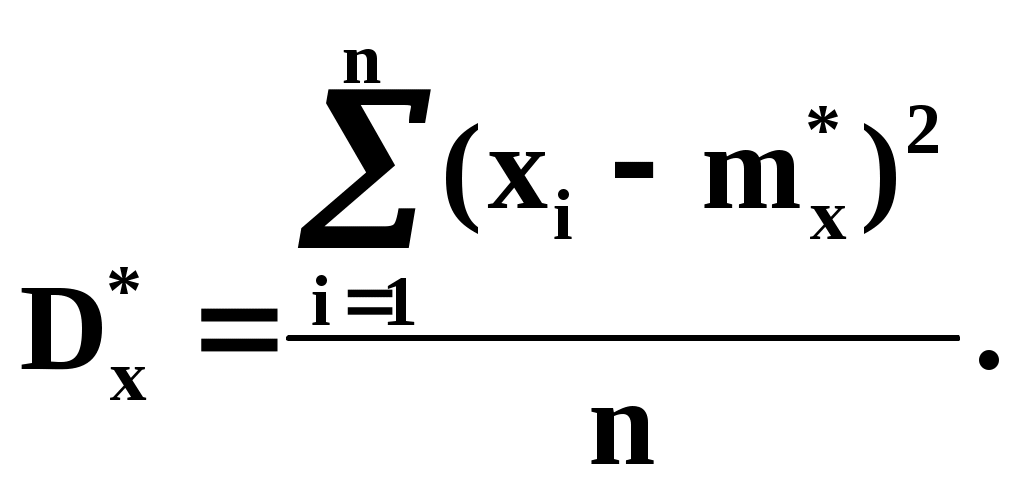 Докажем:  Раскроем правую часть  Таким образом, поставленная задача решена и линейная зависимость, связывающая х и у, имеет вид:  Рассмотрим второй случай. Подбор параметров параболы второго порядка методом МНК  Требуется подобрать по МНК параметры a,b,c квадратичной функции: Дифференцируем по a,b и c:    Подставляем производные в систему: 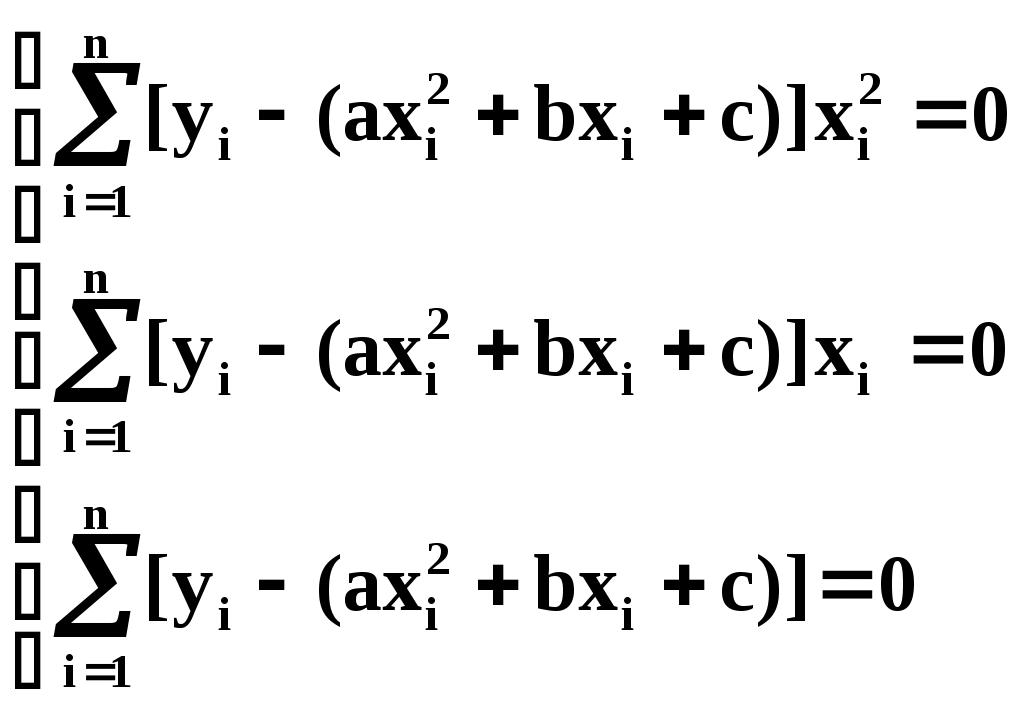 Или раскрывая скобки, приводя подобные члены и деля на n имеем (для простоты будем использовать распространённое в литературе по МНК обозначение вместо 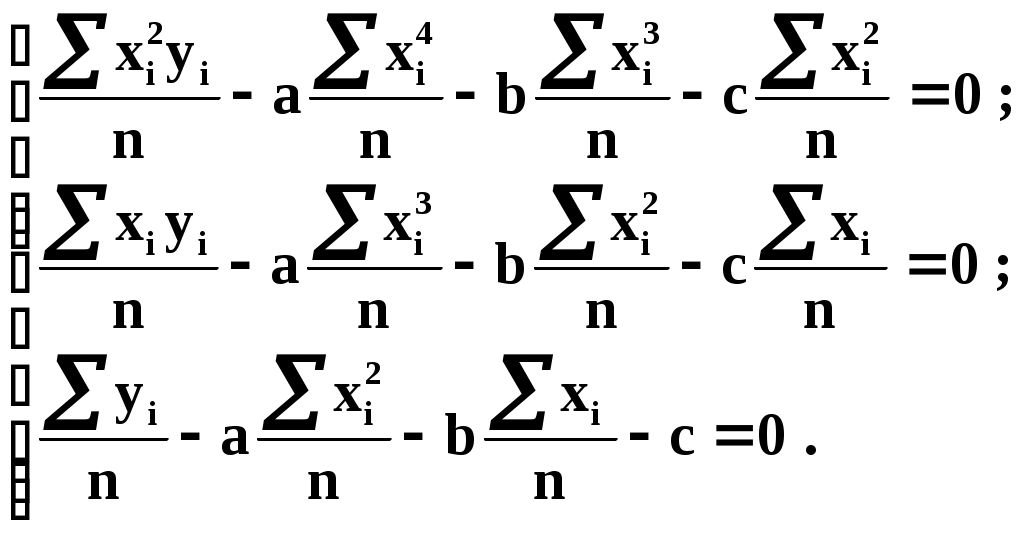 ): Коэффициенты этой системы также представляют собой статистические моменты двух величин X и Y:      С помощью этих начальных моментов можно придать системе более компактный вид. Учитывая, что 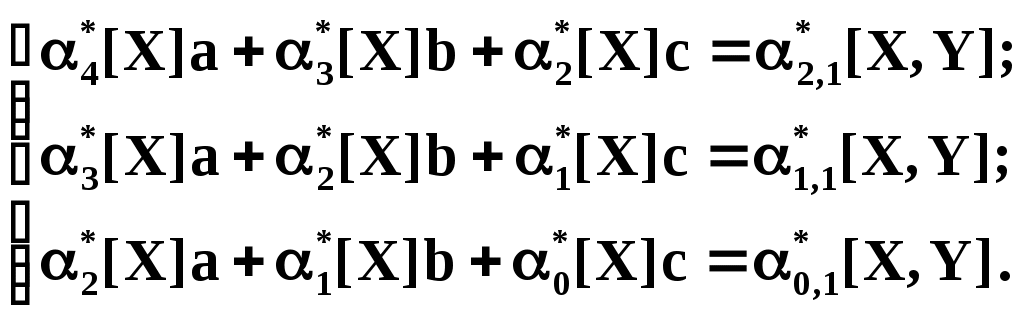  , запишем: Решение этой системы даёт значения a,b,c для искомой функции. Но в общем виде это решение громоздко. Аналогичными по структуре будут уравнения для полинома любого порядка. |