конспект. Основная литература

• Название: Основная литература
• Анкор: конспект
• Дата: 24.01.2023
• Размер: 1 Mb.
• Имя файла: Konspekt_lektsiy.doc
• Тип: Литература; #903309
• страница: 1 из 8

Основная литература

1. 
   Куликовский К.Л, Купер В.Я. Методы и средства измерений. Уч. пособие для ВУЗов. М.: Энергоатомиздат, 1986.– 448с.
   
2. 
   Володарский Е.Т., Малиновский Б.Н., Туз Ю.М. Планирование и организация вычислительного эксперимента. Киев. Высш. школа, 1987.– 280с.
   
3. 
   Ивченко Г.И., Медведев Ю.И. Математическая статистика. Уч. пособие. М.: Высшая школа, 1984, 248с.
   
4. 
   Советов Б.Я., Яковлев С.А. Моделирование систем. Учебник для вузов. М.: Высшая школа, 1985.– 271с.
   
5. 
   Спиридонов А.А., Васильев Н.Г. Планирование эксперимента при исследовании и оптимизации технологических процессов.: Учебное пособие Свердловск.: Изд-во УПИ,1975. - 139 с.
   
6. 
   Вентцель Е.С. Теория вероятностей. Уч. для вузов.– М. Высш. школа, 2001.– 575с.
   
7. 
   Кнут Д. Искусство программирования для ЭВМ. Т.2 Теория вероятностей.– М. Мир, 1977.– 724с.
   

Дополнительная литература

1. 
   Планирование эксперимента в исследовании технологических процессов /К.Хартман, Э.Лецкий, В.Шеффер и др. М.: Мир, 1997.– 552с.
   
2. 
   Кендал М.Дж., Стюарт А. Теория распределений. М.: Наука, 1966.– 587с.
   
3. 
   Хан Г., Шапиро С. Статистические методы в инженерных задачах. М.: Мир, 1969.– 395с.
   
4. 
   Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987.– 599с.
   

Моделирование широко применяется в научных исследованиях и при решении прикладных проблем в различных областях техники. Оно позволяет интенсифицировать действующие производственные процессы путём выявления всех резервов и узких мест, а также за счёт экономии материала и энергии.
Классификация моделей

В качестве основных моделей можно выделить две:

1. Физические модели.

2. Математические модели.

Физическая модель может быть использована, если математическая модель отсутствует или же настолько сложна, что её невозможно исследовать. Например: моделирование в аэродинамических трубах, геометрической формы летательных аппаратов, подводных лодок, автомобилей.

В основе физического моделирования лежит теория подобия. Помимо геометрического подобия (подобия формы) необходимо и физическое подобие моделей и объектов. В соответствующих точках пространства и времени значения физических величин для моделей и объектов должны быть пропорциональными. Это позволяет пересчитать модельные результаты на объект с помощью безразмерных критериев подобия.

Рассмотрим математическую модель, которая является математическим отображением существенных свойств объектов.

Математическая модель представляет собой совокупность уравнений, условий и алгоритмических правил. Она позволяет :

1) получать информацию о процессах, протекающих в объекте;

2) рассчитывать системы, т.е. анализировать и проектировать их;

3) получать информацию для управления моделируемым объектом;

Математические модели можно разделить на два класса:

1) Детерминированные (физико - химические или по-другому теоретические)

2) Вероятностные (стохастические или по-другому эмпирические)

Детерминированные модели отражают детерминированные (закономерные) процессы. Они обычно представляются в виде сложных систем уравнений. Например, системы алгебраических уравнений, системы обыкновенных дифференциальных уравнений, или уравнений в частных производных, а также интегральных уравнений.

Детерминированные модели позволяют довольно точно описать поведение объекта и допускают экстраполяцию в тех точках, где невозможно непосредственное наблюдение. Построение детерминированных моделей связано с проведением научного эксперимента. К детерминированным моделям можно отнести системы автоматического регулирования (САР). Это наиболее быстро развивающийся раздел кибернетики, породивший следующие понятия: обратная связь, частотные методы расчёта, а также структурно-графовые модели.

При моделировании сложных систем классические математические методы оказываются малоэффективными. Здесь играет роль не только сложность системы, но и стохастический (случайный) характер её поведения. Действие большого числа случайных факторов может привести к тому, что отклонения в поведении системы оказываются существенными и не могут быть учтены в виде поправок. Эта проблематика породила вероятностные (статистические) модели. Такие модели получают в результате математической обработки экспериментальных данных, собранных на исследуемом объекте. Структура статистической модели может выбираться достаточно произвольно и может быть относительно простой. Например, часто модели представляются в виде полиномов. Область применения полиномов ограничивается ближайшей окрестностью рабочих точек, в которых проводятся эксперименты.

Во многих случаях построение таких моделей можно выполнить ценой относительно небольших затрат времени и средств. Например, снимается экспериментальная зависимость точки попадания пули (Т) от изменения состава пороха (П). Затем под экспериментальную зависимость T=f(П) подбирается полином y=a+bx+cx²+…, который и является статистической моделью. В кибернетике, также как в физике, химии, используется концепция, при которой различные реальные системы могут быть описаны с помощью одной кибернетической модели. Например: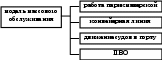



Здесь работа моделей массового обслуживания связана с решением вероятностных задач. Следует отметить, что класс вероятностных моделей сформировался под влиянием статистической физики, методы которой были перенесены в теорию массового обслуживания, теорию надёжности, теорию игр, теорию распознавания образов.

Математические модели можно разделить на:

1) аналоговые (непрерывные);

2) цифровые (дискретные).

Аналоговые модели отражают непрерывные процессы в системах, а цифровые модели служат для описания дискретных процессов.

Дискретные модели используют аппарат дискретной математики и выполняются в виде графов, автоматов (Мили, Мура), а также лингвистических и логических структур.

Математические модели могут быть статическими и динамическими. Статистические модели описывают объект в какой-то момент времени. Динамические модели отражают поведение объекта во времени.

Иногда при исследовании процесса функционирования объектов мат. модели подразделяют на аналитические и имитационные.

При аналитическом моделировании процесс функционирования объекта записывается в виде алгебраических, интегродифференциальных, конечно- разностных соотношений или в виде логических условий. Аналитическая модель может быть исследована двумя методами: аналитическим и численным.

Аналитический, когда характеристики функционирования получают в общем виде; численный, когда решение в общем виде невозможно и стремятся получать числовые результаты для конкретных начальных данных. Численный метод по сравнению с аналитическим позволяет исследовать более широкий класс объектов, но при этом полученные решения имеют частный характер.

При имитационным моделировании имитируется процесс функционирования объекта во времени, причём имитируются элементарные явления, составляющие этот процесс,

с сохранением их логической структуры и последовательности протекания во времени.

Преимущества имитационных моделей по сравнению с аналитическими:

• 
  возможность решения более сложных задач;
  
• 
  возможность быстрого повторного моделирования при новых изменённых режимах и начальных условиях.
  

Однако аналитические модели имеют преимущество при понимании динамики и внутренних закономерностей процесса функционирования объекта, а также при описании мощных дедуктивных методов (дедукция – от общего, сложного к частному, простому).

Вид искомой математической модели зависит как от природы объекта, так и от задачи исследования, а также от требуемой точности и достоверности решения этой задачи.

Дадим классификацию моделей в виде схемы: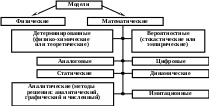


Стратегия построения мат. модели

Рассмотрим построение мат. модели, которое невозможно без знания теории эксперимента. Эксперимент занимает главенствующее место среди способов получения информации об исследуемых объектах. Теория эксперимента даёт нам логическую схему и способ решения задач на разных этапах исследования. Эти этапы образуют стратегию построения мат. модели. Такую стратегию можно представить следующим образом: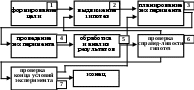



Рассмотрим первый из семи этапов построения модели.

Часто задача эксперимента состоит в том, чтобы определить зависимость между входными и выходными переменными или же найти значения входных переменных (т.е. факторов), которые обеспечивают достижение экстремума какой-либо выходной переменной. Можно сказать, что эти переменные выступают в качестве целевых величин при оптимизации процессов. Дадим классификацию целевых величин, т.е. оптимизируемых переменных моделей: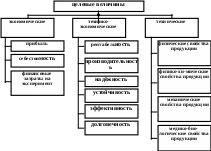


Рассмотрим второй этап построения мат. модели.
Выдвижение гипотез

Под гипотезой (в широком смысле слова) подразумевается некоторое научное предположение о свойствах изучаемых объектов, которое требует проверки и доказательств. Пути формирования гипотез зависят от наличия исходной информации о модели. В зависимости от источника информации о модели различают два их типа. Первый. Это физико-химические модели, иногда называемые теоретическими (или аналитическими). И второй тип. Это статистические модели, называемые иногда эмпирическими.

Для первого типа за основу берутся физико-химические закономерности моделируемых процессов. Например, это уравнения баланса или кинетические уравнения для превращения вещества. Это модели движения, используемые при определении движения летательных аппаратов, а также роботов. Это модели учёта сил межатомного взаимодействия для конструирования атомных ячеек при создании теоретической модели поверхности объекта. Для построения теоретической модели необходимо выяснить природу микропроцессов, протекающих в объекте, и описать их математически. Такие модели обычно представляются в виде систем алгебраических или дифференциальных уравнений. Они довольно точно описывают исследуемые процессы и допускают экстраполяцию в тех точках факторного пространства, где невозможно непосредственное наблюдение.

Модели второго типа – статистические – описывают связь между входными факторами и функцией отклика. Они строятся в результате статистической обработки экспериментальных данных об исследуемом объекте. Структура такой модели выбирается относительно произвольно. Обычно эти модели представляются в виде полиномов. Модели первого и второго типа мы рассмотрели в разделе «классификация моделей».

Рассмотрим третий этап построения мат. модели.
Планирование эксперимента

Латинское слово experimentum – проба, опыт. Это метод познания, при помощи которого исследуются реальные явления действительности, реальные функциональные связи между параметрами изучаемого объекта.

Существующая теория эксперимента даёт экспериментатору ответы на три вопроса. Первый. Как нужно организовать (т.е. спланировать) эксперимент, чтобы решить поставленную задачу наилучшим образом Наилучшим – это в смысле затрат времени и средств или точности результатов. Второй вопрос. Как следует обрабатывать результаты эксперимента, чтобы получить максимальное количество информации об объекте И третий вопрос. Какие основные выводы можно сделать об исследуемом объекте по результатам эксперимента

Основой теории эксперимента является мат. статистика. Она применима для анализа эксперимента в тех случаях, когда его результаты могут рассматриваться как случайные величины или случайные процессы. Это условие выполняется в большинстве исследований, т.к. обычно результаты эксперимента связаны с некоторой неопределенностью. Эта неопределенность возникает из-за случайного характера исследуемых процессов, влияния неконтролируемых факторов, неконтролируемых изменений условий эксперимента и ошибок наблюдений (т.е. измерений).

При статистическом представлении об эксперименте воздействие неконтролируемых факторов рассматривается как дополнительный стохастический шум, наложенный на истинные результаты эксперимента. Чтобы неконтролируемое воздействие сделать случайным, применяют специальные методы, называемые рандомизацией эксперимента. Это позволяет надёжно отделить исследуемые факторы от шумового фона, обусловленного неконтролируемыми воздействиями.

При проведении исследований с целью построения мат. модели, большое значение имеет концепция оптимального использования области варьирования условий эксперимента. С помощью целенаправленного выбора условий, т.е. с помощью планирования эксперимента, можно достигнуть требуемой точности решения при минимальном числе экспериментов. Целенаправленный выбор условий проведения экспериментов предполагает возможность активного воздействия на исследуемый объект, т.е. предполагает активный эксперимент. Обычно такая возможность имеется при лабораторных исследованиях. На промышленных установках, как правило, так действовать нельзя. В этих случаях применяют пассивный эксперимент, т.е. регистрируют факторы в процессе нормальной эксплуатации объекта без целенаправленных воздействий на него.

О зависимостях функциональных, стохастических, статистических корреляционных и регрессионных

Известно множество величин и различного рода параметров, между которыми необходимо устанавливать зависимости, что и является основной задачей эксперимента.

Определим некоторые виды зависимостей между различными величинами и параметрами.

Зависимость называется функциональной (детерминированной), если каждому возможному значению аргумента соответствует определенное значение функции. Это привычные для вас связи, известные из курса мат. анализа:



Связь между случайными величинами, в общем случае, называется стохастической.

Частный случай стохастической связи - связь статистическая.

Связь называется статистической, когда условное мат. ожидание одной случайной величины Y является функцией некоторого значения х другой случайной величины Х.

.

Мат. ожидание величина теоретическая и определить ее можно не всегда, поэтому идут на упрощение и заменяют условное математическое ожидание на условное среднее значение.

Связь называется корреляционной между случайной переменной и условным средним значением другой:


Зависимость называется регрессионной между мат. ожиданием одной величины и определенным значением другой:

.

Но, здесьx - определенное числовое значение (не случайная или условно не случайная).

Уравнение регрессии может быть со многими переменными:

.

Переменные x₁ ... x_n иногда называют факторами.

Эксперимент, в результате которого получают регрессионные зависимости называют факторным экспериментом.

При экспериментальных исследованиях изучаются объекты, которые в общем случае могут быть представлены в виде «черного ящика», на вход которого воздействуют величины, называемые факторами, или независимыми переменными или регрессорами.

Целью экспериментальных исследований является получение зависимости между входными величинами и выходной величиной, называемой функцией отклика. Конечной целью экспериментального исследования является мат. модель, адекватно описывающая поведение объекта.

Если все факторы трактуются как качественные, то применяется дисперсионный анализ. Если же один из факторов качественный, а другие количественные, то применяется корреляционный анализ. Если же все факторы количественные, то для получения мат. модели, связывающей входные и выходные величины, применяется регрессионный анализ. Только полная совокупность результатов эксперимента позволяет судить о поведении случайной величины, оценить характеристики её генеральной совокупности, т.е. получить одно из множества возможных значений всей совокупности оценок. Основной задачей оценивания является получение лучшей среди возможных оценок параметра случайной величины. При этом возможны два варианта.

1) На основании исходных данных получают определенные значения – т.е. точечные оценки, которые максимально стремятся приблизить к значениям соответствующих параметров;

2) Вычисляют граничные значения, между которыми с большой вероятностью должны лежать значения параметров, т.е. строят доверительные интервалы.

В результате точечного оценивания решается, какую величину следует принять в качестве оценки параметра на основании различных критериев минимизации отклонений. При этом полученные точечные оценки параметров должны обладать тремя свойствами: несмещённостью, состоятельностью и эффективностью. Несмещённой называется оценка, мат. ожидание которой равно истинному значению оцениваемого параметра. Состоятельной называется оценка, которая при увеличении выборки стремится к истинному значению. Эффективной называется оценка, которая минимизирует дисперсию отклонения, по сравнению с другими оценками.
Полный факторный эксперимент

Известно, что научные исследования организуются и проводятся настолько хаотично, что их КПД примерно равен двум процентам. Поэтому роль активного эксперимента, значительно повышающего этот КПД, чрезвычайно велика.

План активного эксперимента предусматривает: во первых, число учитываемых входных факторов; во вторых, выбор интервалов варьирования факторов; в третьих, выбор числа уровней варьирования факторов; в четвёртых, выбор сочетаний уровней факторов, их числа и последовательности проведения опытов. Таким образом, план эксперимента предусматривает условия и число проведения опытов, и в значительной мере определяет точность полученной в результате эксперимента мат. модели. Мат. модель получается на основании проведения регрессионного анализа.

Эксперимент, в результате которого все независимые переменные варьируются на всех выбранных уровнях, называется полный факторный эксперимент (ПФЭ). Если эксперименты проводятся только на двух уровнях (т.е. при двух значениях факторах), и в эксперименте осуществляются все возможные комбинации из n факторов, то ПФЭ носит название – типа 2ⁿ.

Обычно факторы различны по физической природе и изменяются в различных динамических диапазонах. Поэтому для формализации процесса анализа и независимости полученных результатов от изменения масштаба входных величин – факторы предварительно кодируют. Для этой цели используют соотношение:



где и – граничные значения варьирования независимыми переменными, которые или заданы или выбираются экспериментатором. Таким образом, операция кодирования независимых переменных заключается в переносе центра координат в точку х_jср, называемую центром плана эксперимента. В кодированной системе на основании выражения (1) будут соблюдаться соотношения: