конспект. Основная литература

• Название: Основная литература
• Анкор: конспект
• Дата: 24.01.2023
• Размер: 1 Mb.
• Имя файла: Konspekt_lektsiy.doc
• Тип: Литература; #903309
• страница: 5 из 8

результатов измерений

Разнообразие задач, решаемых с помощью измерений, определяет разнообразие видов обработки результатов измерений. Так как все измерения сопровождаются случайными погрешностями, то обработка результатов измерений всегда включает в себя операции над случайными величинами или процессами, выполняемые на основе методов теории вероятностей и мат. статистики. Типичными являются следующие задачи:

1. 
   обработка результатов косвенных измерений;
   
2. 
   обработка результатов совместных измерений;
   
3. 
   обработка результатов неравноточных измерений.
   

В процессе обработки находятся оценки определяемых параметров, строятся доверительными интервалы для истинных значений параметров. Эти построения исходят из предположения о законе распределения погрешности, её мат. ожидании и дисперсии и о независимости отдельных наблюдений .
Обработка результатов прямых измерений

Предположим, что истинное значение измеряемой величины равно A и выполнено n аналогичных измерений, результаты которых равны x₁,…,x_n. Каждый результат x_i называют результатом наблюдения. Результатом измерения будет оценка значения измеряемой величины. Разность есть погрешность i-го наблюдения. Относительно погрешности сделаем следующие допущения:

1. 
   Погрешность является случайной величиной с нормальным законом распределения .
   
2. 
   Систематическая погрешность отсутствует, т.е. мат. ожидание погрешности .
   
3. 
   Измерения равноточные, т.е. погрешность имеет дисперсию , одинаковую для всех измерений.
   
4. 
   Погрешности отдельных наблюдений независимы.
   

Методы обработки результатов прямых измерений

Рассмотрим прежде всего статистические измерения (т.е. многократные наблюдения). Результат каждого наблюдения даёт оценку измеряемой величины. Результат наблюдения отличается от истинного значения из-за случайной и систематической составляющих погрешности:

.

Повторяя наблюдения, мы получаем информацию о случайной погрешности. О систематической погрешности из самих наблюдений информацию извлечь нельзя. Чтобы оценить эту погрешность, надо знать свойства используемых средств измерений, метод и условия измерения. Предположим, что систематическая погрешность результата каждого наблюдения известна. Тогда, введя поправки , вместо группы получим группу исправленных результатов наблюдений:



Наша задача – найти оценку . Математически обоснованное решение, отвечающее требованиям несмещённости, состоятельности и эффективности, можно найти зная вид распределения .

Часто погрешности измерений имеют нормальное распределение. Предположение о нормальном законе распределения погрешностей обосновывается центральной предельной теоремой теории вероятностей, согласно которой сумма большого числа случайных величин с соизмеримыми дисперсиями имеет в пределе нормальное распределение.

Поскольку погрешность измерения обусловлена большим количеством факторов, т.е. формируется как сумма большого количества слагаемых – воздействий случайных факторов, то условия теоремы выполняются, и погрешность имеет нормальное распределение. То же самое распределение имеют и результаты наблюдений.

При нормальном распределении наблюдений оптимальной оценкой центра распределения А является среднее арифметическое результатов наблюдений:



Если систематические погрешности 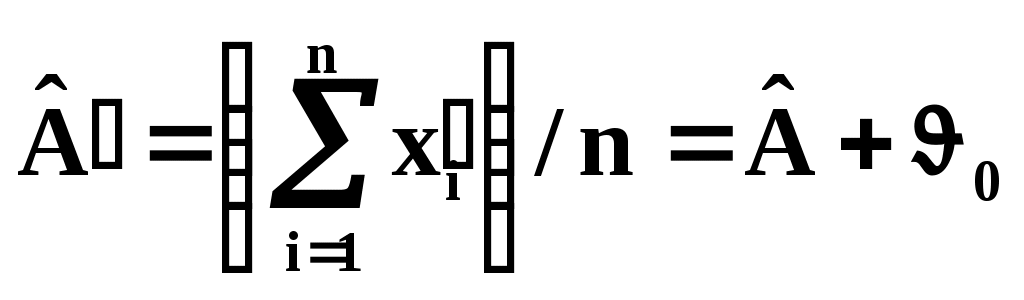, т.е. они постоянны, то можно не исправлять результатов наблюдений, а сначала вычислить предварительный результат измерения:

,

и затем найти

.

Среднее арифметическое обладает одним очень важным свойством: сумма квадратов отклонений от среднего арифметического минимальна. Для доказательства рассмотрим функцию:

.

Найдём из услови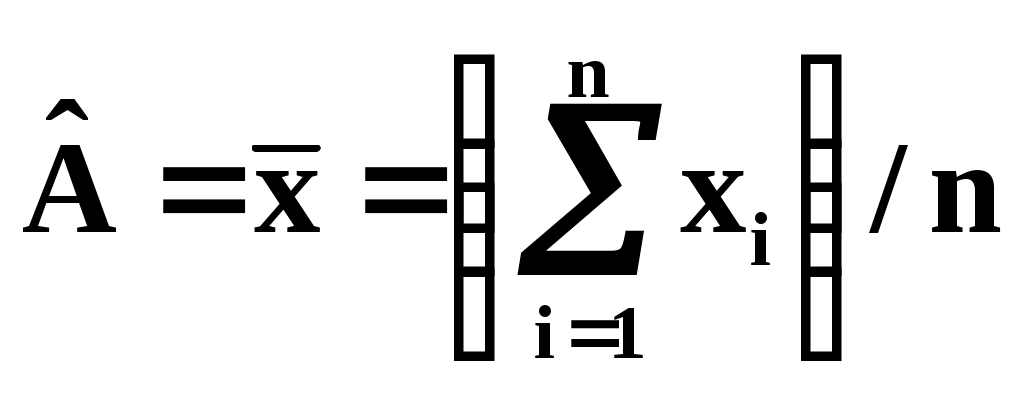я минимизации Q. Воспользуемся необходимым условием экстремума:



Тогда

;

или

,

т.е. при имеем Q=min.

Таким образом, в качестве оценки измеряемой величины имеем среднее арифметическое. Из-за случайных погрешностей результаты наблюдений также являются случайными величинами, и если выполнить ещё одну серию наблюдений, то полученное новое среднее арифметическое будет несколько отличаться от ранее найденной оценки. Это рассеивание средних арифметических характеризуется или дисперсией средних арифметических или средним квадратическим отклонением. Оценку СКО среднего арифметического находят по формуле: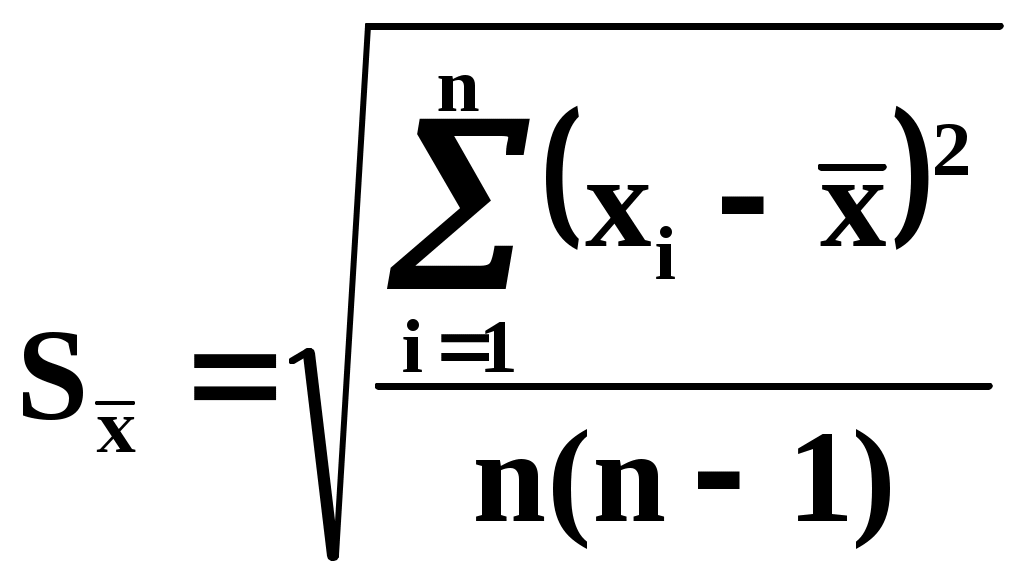

;

Кроме того, для А можно построить доверительный интервал, определяющий доверительные границы случайной погрешности результата измерения. Доверительный интервал определяется неравенствами:


(13)

(14)
,

где ; – критерий Стьюдента. t_q-q – процентная точка распределения Стьюдента, зависящая от доверительной вероятности  и числа степеней свободы k=n-1. Таким образом, случайная погрешность  с вероятностью, равной доверительной вероятности , лежит в границах ; .

С систематическими погрешностями дело обстоит иначе. Смещённость результата измерения, которую характеризуют систематические погрешности, можно оценить:

1. 
   либо с помощью более точных средств измерений;
   
2. 
   либо по косвенным данным, включая данные метрологических свойств измерений.
   

Первый вариант – использование более точных средств измерений используется только в поверочной практике, а в других случаях использовать приборы с разным классом точности нецелесообразно. Поэтому основным является второй вариант, когда систематическая погрешность оценивается по косвенным данным. Для этого выясняют все возможные источники погрешностей, оценивают по отдельности погрешности, вызванные каждым из них, т.е. оценивают все элементарные погрешности, и их суммируют.

При прямых измерениях с точным оцениванием погрешностей всегда можно различать два типа средств измерений:

1. 
   основные, дающие оценку измеряемой величины;
   
2. 
   средства измерений влияющих величин.
   

Для основных средств измерений находят оценки их систематических погрешностей. При этом случайные погрешности можно вообще не оценивать, т.к. они войдут в результаты наблюдений, и будут учтены при их обработке.

Далее находят функции влияния тех влияющих величин, которые при измерении могут оказаться за пределами их нормальных значений. Установив таким образом индивидуальные свойства основных средств измерений, далее при эксперименте измеряют все влияющие величины. Например, если для влияющей величины получена оценка , а коэффициент её влияния , то оценка систематической погрешности, обусловленная этой величиной, будет

.

Алгебраическая сумма всех найденных оценок элементарных систематических погрешностей даёт поправку: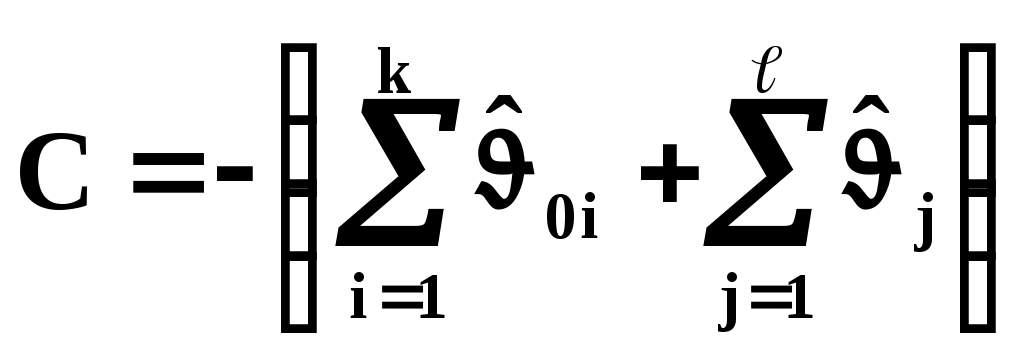

,

где – оценка систематической погрешности i-го основного средства измерений в нормальных условиях.
Косвенные измерения

Это измерения, при которых искомое значение величины находят путём согласованных измерений других величин, связанных с измеряемой величиной известной зависимостью. Эти другие величины будем называть измеряемыми аргументами. Измеряемая величина (т.е. её истинное значение А) связана с измеряемыми аргументами А_i (где i=1…m) зависимостью, которую обычно можно разрешить относительно А, т.е. представить в виде:

А=f(A₁,…,A_m)

Случаи неявной зависимости между А и А_i нетипичны. Если зависимость линейная, то она выражается в виде:



где b_i – постоянный коэффициент i-го аргумента А_i. Если зависимость нелинейная, то её можно записать в общем виде как:


Линейные косвенные измерения

т.е. описываемые формулой:

(1)

Если взять случайную величину Y, связанную линейной зависимостью со случайными величинами X_i: т.е. то

.

Поэтому, располагая оценками аргументов А_i, за оценку измеряемой величины А естественно принять



где будет несмещённой и состоятельной при таких же . Кроме того:

,

т.е. если оценки обладают минимальной дисперсией (а значит являются эффективными), то и оценка будет эффективной. Каждая полученная оценка обладает некоторой фиксированной погрешностью , где ; – систематическая составляющая погрешности; – случайная составляющая. Тогда

(2)

Из (2) найдём погрешность  косвенного измерения с учётом (1):

, или



Таким образом, при косвенных измерениях путём суммирования составляющих приходится находить не только границы систематической погрешности результата (как при прямых измерениях), но и случайные погрешности.

Рассмотрим сначала случайные погрешности. Случайную погрешность результата косвенного измерения можно считать нормально распределенной. И если число наблюдений превышает 25-30, то доверительная граница случайной погрешности  результата будет равна:

,

где – квантиль нормированного нормального распределения, соответствующий доверительной вероятности  (находится по таблицам); – оценка С.К.О. результата измерения. – оценка дисперсии результата измерения; – оценка дисперсии измерения i-го аргумента.

Теперь рассмотрим задачу оценивания систематической погрешности. Эти погрешности учитываются путём введения поправок. Реализация неисключённых систематических составляющих должна иметь свои границы возможных значений . Если две составляющие общей погрешности  считать нормально распределёнными (а это оправдано, когда число слагаемых велико, и все границы вычислены для одной доверительной вероятности ), то в этом случае:


Обработка результатов косвенных

измерений

Дано: A=F(A₁,A₂,…A_m);

Пусть каждая из величин А_j j=(1,…m) измерена с погрешностью _j. Необходимо оценить значение погрешности А результата косвенного измерения. Рассмотрим полный дифференциал:



или

Заменив дифференциалы соответствующими приращениями, для погрешности получим:



Если и погрешности некоррелированы, то

Рассмотрим пример 1. Пусть наша функция линейна и имеет вид:



где известные коэффициенты. Тогда ; ;

Рассмотрим пример 2. Пусть наша функция логарифмируема и имеет вид:



где – известные величины. Прологарифмируем, а затем продифференцируем нашу функцию



Положив погрешности измерений малыми, заменив в (3) дифференциалы соответствующими приращениями:



где – относительные погрешности. Дисперсия случайной относительной погрешности равна:



Видно, что в данном случае расчёт погрешностей упрощается при переходе к оценкам относительных погрешностей измерений.