конспект. Основная литература

• Название: Основная литература
• Анкор: конспект
• Дата: 24.01.2023
• Размер: 1 Mb.
• Имя файла: Konspekt_lektsiy.doc
• Тип: Литература; #903309
• страница: 3 из 8

u - номер параллельного опыта в центре плана;

Y_0u- значение функции отклика;

N - число опытов в матрице планирования;

j - номер опыта в матрице планирования;

i,l - номера факторов;

X_ij, X_lj - кодированные значенияi-го и l-го факторов в j-м опыте;

Y_j - значение функции отклика вj-м опыте;

k - число факторов;

A, B, C, D, p - константы, зависящие от числа факторов. При трех факторах A= 1/8, B = 1/4, C = - 1/16, D = 1/4, p = 2.
Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численное значение коэффициента, тем большее влияние оказывает фактор.

Если коэффициент имеет знак плюс, то с увеличением значения фактора выходная величина увеличивается, а если минус, то уменьшается. Значение коэффициента соответствует вкладу данного фактора в размер выходного параметра при переходе фактора с нулевого уровня на верхний или нижний.

Дисперсии коэффициентов уравнений регрессии найдем по формулам:

; ; ; ; B₁ = 13/ 48.
ДисперсиюS²_Y воспроизводимости эксперимента вычислим по результатам опытов в центре плана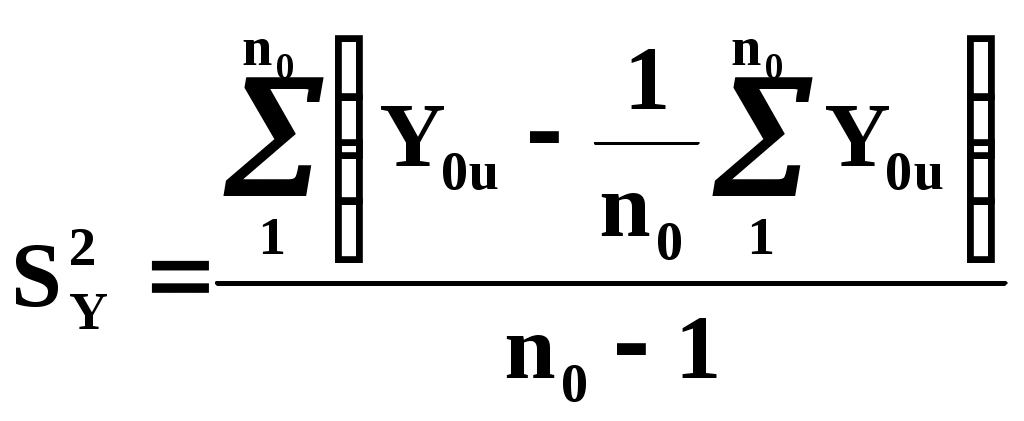

.

Доверительные интервалы для определения значимости коэффициентов уравнений регрессии находились по формулам:

.

Табличное значение критерия Стьюдента при числе степеней свободы, равном двум, и 5% уровне значимости t = 4,3. Тогда, соответствующие значения доверительных интервалов:

b₀ =  0,062; b_i =  0, 038; b_il =  0, 054; b_ii =  0, 056.

Сравнение значений доверительных интервалов со значениями коэффициентов уравнения регрессии (44.6) позволяет перейти к следующему виду регрессионной модели:

.

Адекватность модели может быть установлена по критерию Фишера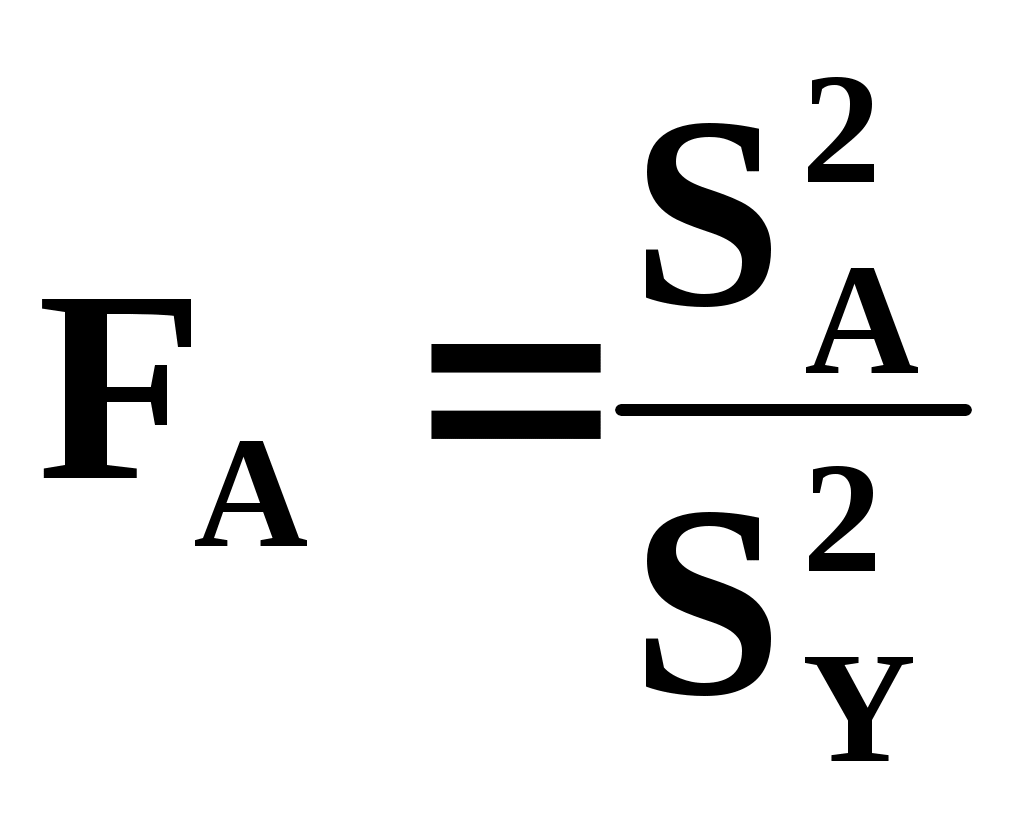

.

Дисперсию адекватности найдем по формуле: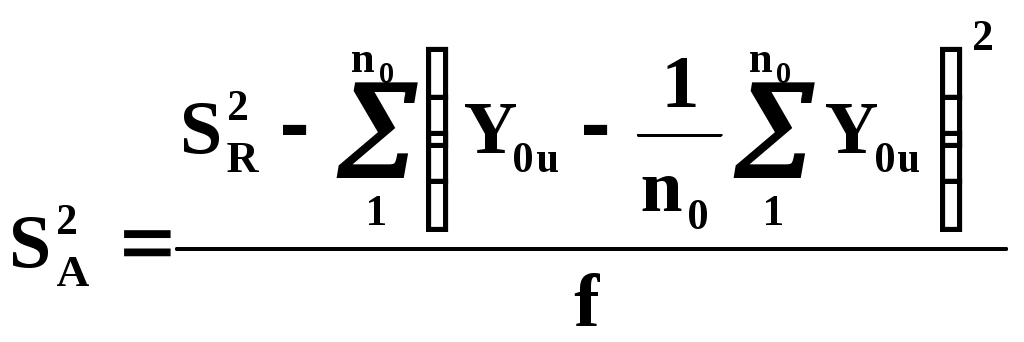

,

где S_R² - сумма квадратов отклонений эмпирических значений функции отклика от ее значений, вычисленных по модели, во всех точках плана;

f- число степеней свободы, ;

k₁ - число коэффициентов аппроксимирующего полинома.

В нашем случае S²_Y = 0, 000632, а S_А² = 0,00371, отсюда F_A = 5,868 при табличном значении F_T = 19,3. Таким образом, построенная регрессионная модель адекватна и может быть использована для анализа изменения функции отклика.
Рассмотрим 4-й этап построения мат. модели.

Проведение эксперимента

Формально под экспериментальным исследованием можно понимать поиск функциональной зависимости между параметрами, описывающими состояние системы, а также феноменологическое описание или объяснение обнаруженных новых закономерностей.

Экспериментальное исследование состоит по крайней мере из трёх этапов. Это: измерение, аналитическое описание и феноменологическое объяснение результатов.

Два первых этапа не очень сильно связаны с природой объекта и имеют много общего для различных объектов. Дать же феноменологическое объяснение результатов может только специалист в данной области знаний.

Обычно эксперимент проводится на специальных исследовательских установках. При проведении сложного эксперимента с большим количеством факторов и тысячами регистрируемых событий невозможно обойтись без средств автоматизации измерений и обработки результатов.

Рассмотрим автоматизацию эксперимента. Опыт показывает, что системы автоматизации экспериментальных исследований (САЭИ) перестали быть вспомогательным инструментом. Их отсутствие в настоящее время уже невозможно компенсировать изобретательностью и находчивостью экспериментатора. САЭИ называется программно-аппаратный комплекс на базе средств измерительной и вычислительной техники. Он предназначен для проведения научных исследований или же комплексных исследований новой техники на основе получения и использования моделей исследуемых объектов, явлений и процессов, а также натурных испытаний. Схему САЭИ можно представить следующим образом: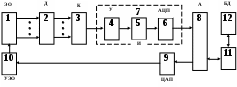




Расшифруем обозначения в схеме: 1 – экспериментальный объект; 2 – датчики; 3 – коммутатор; 4 – усилители; 5 – интегратор; 6 – АЦП; 7 – измерительная система; 8 – адаптеры, интерфейсы; 9 – ЦАП; 10 – управление экспериментальным объектом; 11 – ЭВМ; 12 – база данных.

По данной схеме отметим следующие моменты. Датчики измерительной системы обычно бывают аналогового типа. Это датчики температуры, давления, тока, напряжения, перемещения и т.д. Если сигнал неэлектрический, то его преобразуют в электрический. Слабые сигналы усиливают. Для подключения нескольких датчиков к одному усилителю применяют коммутатор. Измерительная система преобразует аналоговые сигналы в цифровую форму с помощью АЦП. Для возможности соединения блоков между собой выработаны стандарты на сопряжения, т.е. интерфейсы. Главный интерфейс системы – это стык между ЭВМ и измерительной частью. Если блоки, подключаемые к ЭВМ, не имеют стандартного интерфейса, то они подключаются через адаптеры, т.е. через переходники.
Автоматизированные системы обработки информации и управления

Кратко перечислим возможные автоматизированные системы.

Это АСНИ – автоматизированные системы научных исследований.

Это АСУТП – автоматизированные системы управления технологическими процессами.

Это САНЭ – системы автоматизации научных экспериментов.

Это АСКИО – автоматизированные системы контроля, испытаний и обработки.

Это ИВК – измерительно-вычислительные комплексы.

Существуют и другие системы специального назначения, обработки информации и управления. Переход к автоматическим измерениям связан с отсутствием сведений о требуемой точности измерений, с необходимостью перехода от оценок, удобных при ручной обработке результатов измерений, к оптимальным оценкам. При этом под оптимальной системой автоматического управления понимается наилучшая в некотором определённом смысле система.
Критерии оптимальности моделируемой системы

Критерии оптимальности, на основе которых строится система, могут быть самыми разными, и зависят от специфики решаемой задачи. Критериями оптимальности могут быть: точность системы, её экономичность, производительность, быстродействие, стоимость и другие технико-экономические показатели.

Следует отметить противоречивость многих критериев, например: устойчивость и точность, точность и стоимость. Чем лучше одно, тем хуже другое. Принимая решение в противоречивой ситуации, мы идём на компромисс, например между устойчивостью и точностью. Поэтому все практические задачи – это задачи с ограничениями. Например, ограничена область допустимых значений переменных: мощность, стоимость и т.д.

При отсутствии ограничений значение такой функции можно формально уменьшать до нуля, или увеличивать до бесконечности, но при этом не получать оптимального решения. Неформальная сторона задачи заключается в выборе критерия и ограничений (т.е. допустимых значений).

Выход из тупика заключается в волевом решении на основании соображений «здравого смысла», критерием которого может быть сложившаяся практика до автоматизации. Как только критерий выбран, а его значение принято, так далее следует формальное (т.е. математическое) решение задачи создания модели, т.е. математической зависимости, адекватно описывающей объект с точки зрения интересующих нас его свойств.

Следует отметить, что не всякая задача имеет решение. По А.Н.Тихонову задача корректна, если выполняются три условия:

1) существование решения;

2) однозначность решения;

3) устойчивость решения;

(Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач.– М.: Наука, 1974). Два первые требования понятны. Решение должно существовать, его можно найти, и это решение должно быть единственным. Третье условие означает, что малым возмущениям исходных данных должны соответствовать малые изменения решения.
Идентификация моделей.

Идентификация – это определение параметров и структуры мат. модели, обеспечивающих наилучшее совпадение выходных координат модели и процесса при одинаковых входных воздействиях. Таким образом, процедура идентификации распадается на три этапа:

1-й этап. Выбор структуры модели на основании априорной информации об исследуемом процессе (отметим, что структура модели – это её компоненты, переменные, параметры, функциональные зависимости, ограничения, целевые функции);

2-й этап. Выбор критерия близости, основанный на специфике задачи;

3-й этап. Определение задачи параметров модели, оптимальных с точки зрения выбранного критерия близости.

По В.В.Фёдорову в зависимости от априорной информации различают три уровня информированности экспериментатора (Фёдоров В.В. Теория оптимального эксперимента.– М.: Наука, 1971):

1) Мат. модель известна и требуется уточнить или определить неизвестные параметры модели;

2) Мат. модель совпадает с одной из функций и нужно выбрать одну из них;

3) Вид мат. модели неизвестен, возможна аппроксимация конечным рядом, например, полиномом.

Задача идентификации имеет стохастический характер из-за неучёта вектора случайных возмущений, например, ошибок измерений. Из-за стохастического характера в основу идентификации естественно положить принцип максимума апостериорной (т.е. после опыта; априорной – т.е. до опыта) вероятности, т.е. метод максимального правдоподобия.

Он позволяет найти состоятельные оценки, распределённые асимптотически нормально и имеющие наименьшую дисперсию по сравнению с другими, также асимптотически нормальными оценками. Отметим, что фраза «распределённые асимптотически нормально» означает: распределенные нормально для выборок с неограниченно возрастающим объёмом. Суть метода максимума правдоподобия заключается в следующем. (на пальцах):

Пусть в результате опыта, т.е. ряда измерений произошло следующее событие, а именно: случайные величины (Y₁,Y₂,…,Y_n) приняли совокупность значений (y₁,y₂,…,y_n). Задача – так подобрать мат. ожидания (х₁), (х₂),…, (х_n), чтобы вероятность этого события была максимальной. Это так называемый принцип максимального правдоподобия. Поэтому метод максимального правдоподобия заключается в решении системы уравнений: (i=1,2,…k), где _i – неизвестный оцениваемый параметр, а L – функция правдоподобия. Функция правдоподобия L для случая выборки объёма n выражается произведением: , где – плотность распределения одномерной генеральной совокупности; ₁,…_к – неизвестные оцениваемые параметры; x_r – значения элементов выборки. Решением являются k корней этой системы уравнений, которые зависят от значений выборки. Фактически функция правдоподобия L обозначает совместную плотность распределения вероятностной выборки, а искомые оценки ₁,…_к строятся так, что если их подставить в формулу для L, то достигается максимум плотности вероятности выборки . Построение таких оценок достигается приравниванием нулю. Полученные таким образом решения системы уравнений (i=1,2,…k) и служат оценками параметров ₁,…_к.

Ввиду отсутствия достаточно надёжной информации о характере связей между ошибками опытных данных, и о законах их распределения, а также из-за сложности вычислений и громоздкости алгоритмов вместо метода максимального правдоподобия применяют метод наименьших квадратов (МНК).

Принципиальное отличие МНК от метода максимального правдоподобия состоит в том, что он не требует знания вида закона распределения ошибок измерений. Оба эти метода получили в практике наибольшее распространение.

Следует отметить, что в случае нормального распределения ошибок, решения с помощью обоих методов совпадают.

Рассмотрим пример использования МНК.

Допустим, что мы имеем дело с (к+1)-мерным пространством переменных х₁,…х_к,у. По методу наименьших квадратов, в этом пространстве проводится гиперповерхность, сумма квадратов отклонений от которой минимальна. Эта гиперповерхность строго проходит через точки дополнительных условий. Представим для примера, что мы аппроксимируем поверхность крыла, кузова автомобиля по экспериментальным точкам, полученным путём обмера плазовой модели. Эта поверхность должна строго проходить через граничные точки (т.е. точки сопряжения с другими элементами объекта), что и обеспечивается учётом дополнительных условий.
Вычислительный эксперимент.

Если удаётся выразить весь моделируемый процесс в форме математических уравнений и отношений, то их можно исследовать на ЭВМ. Математическое моделирование – это специфический эксперимент на основе полной автоматизации.

Иногда численное решение уравнений мат. модели называют вычислительным экспериментом, поскольку оно имеет много общего с натурным экспериментом. Но в отличие от натурного вычислительный эксперимент имеет в своей основе не реальный физический объект, а его мат. модель и реализуется не через измерение определённых величин, а через их вычисление с помощью компьютерных программ.

Вычислительный эксперимент, как и натурный является средством изучения реальных объектов, приводящим к пониманию физики объекта и получению его числовых характеристик. Он является как бы «зеркальным» отображением натурного эксперимента.

Использование ЭВМ и наличие –огромного количества мат. пакетов значительно упрощает использование численных методов. Современное программное обеспечение ЭВМ позволяет реализовывать численные методы интегрирования и дифференцирования, интерполяции и приближения функций, решения систем различных типов алгебраических и дифференциальных уравнений, исследование устойчивости и т.д.

Развитие вычислительной техники приводит к созданию программных комплексов, при использовании которых отпадает необходимость в программировании метода решения, т.е. достаточно лишь ограничиться заданием исходной информации. Это существенно снижает требования к знакомству пользователя ЭВМ с численными методами, но не устраняет полностью необходимости знакомства с вычислительным процессом.

Программные комплексы

мат. расчётов и моделирования

К числу современных пакетов прикладных программ (ППП), использующихся при мат. расчётах и моделировании, относятся: Scientific Work Place, Derive, MathCAD, Matematica, MatLAB и др. Все ППП имеют общий и хорошо известный из опыта работы с текстовыми и графическими редакторами набор файловых операций, вставки и удаления фрагментов, настройки системы, обеспечение справочной информацией. В них предусмотрены арифметические и логические операции, вычисление алгебраических и тригонометрических функций, решение систем алгебраических и дифференциальных уравнений и т.д. Новое поколение интегрированных ППП освоило и символьную форму представления уравнений, которая позволяет осуществлять перестановки, проводить операции с полиномами, разлагать функции Тейлора, решать дифференциальные уравнения и т.д.

Перечисленные возможности реализуются и в численной форме, а также используются в комбинации, когда сложное выражение преобразуется аналитически. В состав ППП входят также графические средства представления расчётов. Использование графических средств очень полезно, т.к. наш глаз способен выделять структуры и тренды, незаметные из табличных данных, а также обнаруживать изменения во времени, которые могут привести к пониманию важных механизмов, лежащих в основе поведения объекта. Они могут вычерчиваться как на плоскости, так и в пространстве в различных системах координат (т.е. в декартовой, в полярной, в цилиндрической и в сферической).
Метод статистических испытаний (метод Монте-Карло)

Одной из разновидностей мат. моделирования как чистого эксперимента является моделирование стохастических процессов. Это метод статистических испытаний или метод Монте-Карло, названный по аналогии с игрой в рулетку во всемирно известном казино Монте-Карло в Монако. Метод основан на многократном моделировании процесса при случайных воздействиях со статистической обработкой результатов испытаний (т.е. моделирования).

Хотя наибольшую пользу выборочный метод Монте-Карло приносит при моделировании вероятностных ситуаций, он приложим также и к некоторым полностью детерминистским задачам, не имеющим аналитического решения .

В методе Монте-Карло данные предшествующего опыта вырабатываются искусственно путем использования некоторого генератора случайных чисел в сочетании с интегральной функцией распределения вероятностей для исследуемого процесса. Таким генератором может быть таблица, колесо рулетки, подпрограмма ЭВМ или какой-либо другой источник равномерно распределенных случайных чисел.

Подлежащее разыгрыванию распределение вероятностей может быть основано на эмпирических данных, извлекаемых из ранее сформированных записей, или на результатах последнего эксперимента, либо может представлять собой известное теоретическое распределение. Случайные числа используются для получения дискретного ряда случайных переменных, имитирующего результаты, которых можно было бы ожидать в соответствии с разыгрываемым вероятностным распределением.

Способ применения метода Монте-Карло по идее довольно прост. Чтобы получить искусственную случайную выборку из совокупности величин, описываемой некоторой функцией распределения вероятностей, следует:

1. Построить график или таблицу интегральной функции распределения на основе ряда чисел, отражающего исследуемый процесс (а не на основе ряда случайных чисел), причем значения случайной переменной процесса откладываются по оси абсцисс (х), а значения вероятности (от 0 до 1)—по оси ординат (y).

2. С помощью генератора случайных чисел выбрать случайное десятичное число (СЧ) в пределах от 0 до 1 (с требуемым числом разрядов).

3. Провести горизонтальную прямую от точки на оси ординат, соответствующей выбранному СЧ, до пересечения с кривой распределения вероятностей.

4. Опустить из этой точки пересечения перпендикуляр на ось абсцисс.

5. Записать полученное значение х. Далее оно принимается как выборочное значение.

6. Повторить шаги 2—5 для всех требуемых случайных переменных, следуя тому порядку, в котором они были записаны.

Метод статистического моделирования Монте-Карло применяется для исследования и анализа характеристик радиокомпонентов при значительных отклонениях параметров от их средних значений (например, в программах Pspice, Electronics Workbench, и др.). Следует отметить, что в случае больших отклонений х_i входных параметров применение приближенных расчетных формул, полученных при использовании вероятностно-статистического метода анализа точности, приводит к значительным погрешностям полученных результатов.

Применение метода Монте-Карло позволяет получить функцию распределения плотности вероятности параметров радиокомпонентов. По графику этой функции можно определить не только среднее значение выходного параметра, но и предельные отклонения параметра, а также вероятность попадания параметра в заданные границы поля допуска.

При использовании метода статистического моделирования исследованию может подвергаться любая аналитически заданная функция вида

y = f(x₁, x₂,…x_n) .

Объем вычислений при этом существенно увеличивается и для расчетов используется ЭВМ.

В качестве примера исследуем методом Монте-Карло функцию, выражающую зависимость выходного параметра радиокомпонента у от комплексного воздействия дестабилизирующих факторов (температуры, времени, влажности):



где y_н – номинальное значение параметра; _y,T – температурный коэффициент; _y,t – коэффициент старения; _ - коэффициент влажности.

Значениями дестабилизирующих факторов являются: T – изменение температуры; t – промежуток времени, для которого рассчитывается изменение параметра у; значение влажности окружающей среды, косвенно задаваемое через величину коэффициента влажности _.

Значения дестабилизирующих факторов (T, t, и влажности) являются детерминированными, т.е. неслучайными величинами.

Сущность метода Монте-Карло для анализа отклонения параметров радиокомпонентов может быть выражена в виде следующего алгоритма:

1. Рассчитывается или задается объем выборки радиокомпонентов N, необходимый для обеспечения достаточной точности проведения расчетов.

2. Измеряется N значений исследуемого параметра y_n радиокомпонента, а также определяется N значений входных параметров (в данном случае коэффициентов нестабильности).

3. В расчетную формулу случайным образом подставляются значения , и значения коэффициентов нестабильности .

4. После проведения N расчетов получаем N случайных значений параметра у.

Дальнейшая обработка полученных данных заключатся в проведении вычислений и графическом представлении результатов.

Среднее значение параметра у рассчитывается по формуле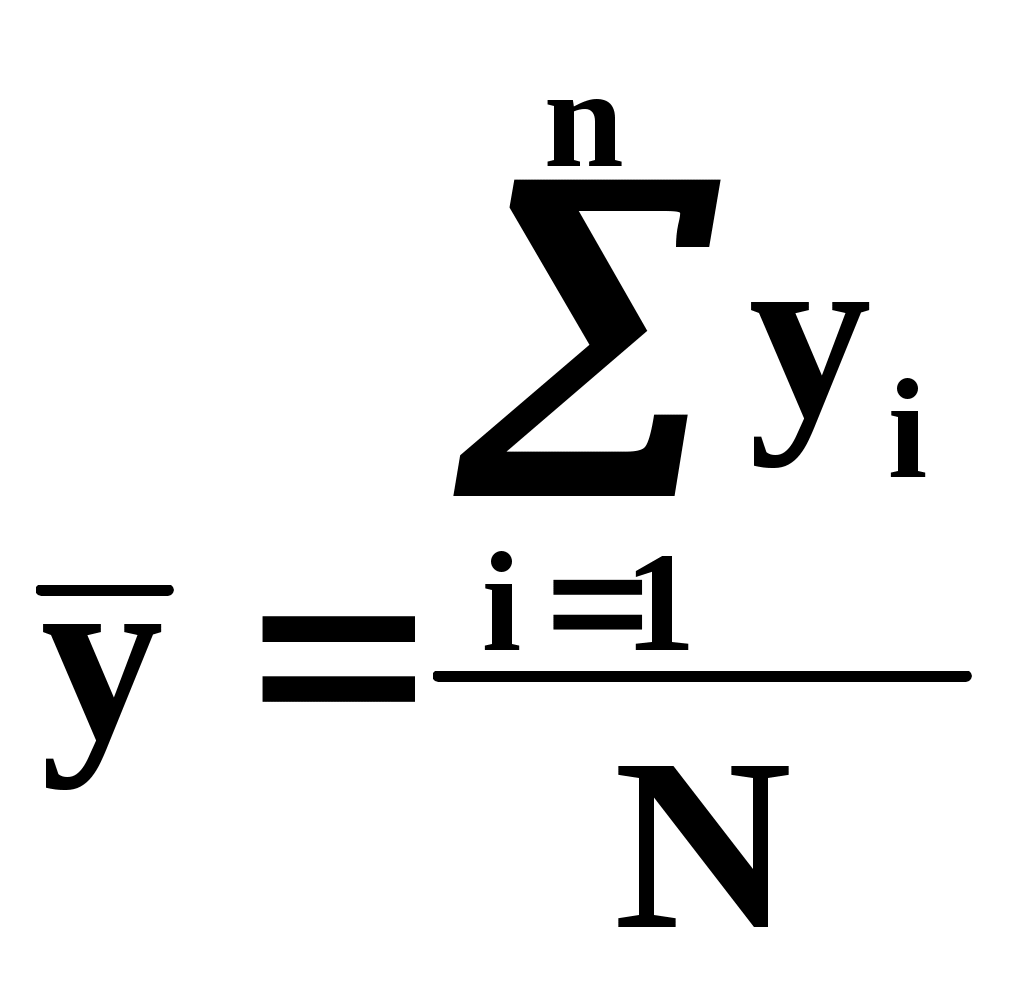



При работе с выборками конечного объема для оценки отклонения среднего значения параметра у пользуются понятием выборочного среднеквадратического отклонения S_y.

Выборочное среднеквадратическое отклонение S_y определяется из выражения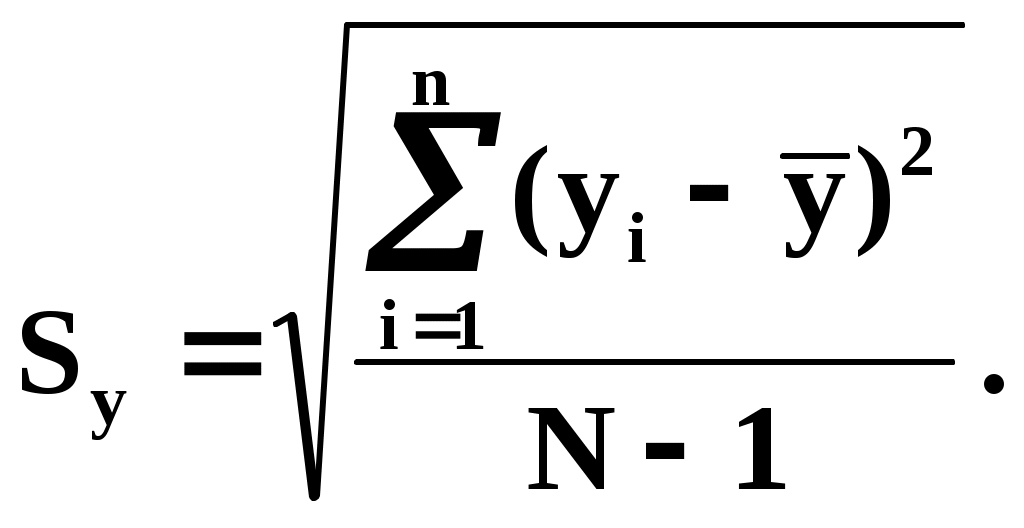



В предположении о нормальном законе распределения относительное предельное отклонение параметра у под влиянием дестабилизирующих факторов рассчитывается из соотношения



Абсолютное изменение величины предельного отклонения параметра (у) можно оценить по формуле

(у) = у - у_TУ ,

где у_TУ - половина границы поля допуска параметра по ТУ.

Для оценки доли радиокомпонентов, пригодных к дальнейшей эксплуатации, следует построить гистограмму распределения параметра у.

Для определения доли радиокомпонентов, пригодных к дальнейшей эксплуатации, следует на гистограмме указать границы поля допуска радиокомпонентов по ТУ. Сумма относительных весов (частостей) соответствующих интервалов, оказавшихся внутри границ поля допуска по ТУ, даст значение вероятности попадания значений параметров радиокомпонентов в указанный диапазон.
Вычисление интегралов методом статистических испытаний

(или методом Монте-Карло).

Задачи, связанные с вычислением многократных интегралов, могут быть эффективно решены методом статистических испытаний, особенно в тех случаях, когда к точности результатов расчёта не предъявляются очень жёсткие требования. Рассмотрим простейший пример для случая одного измерения.

Пусть  – непрерывная случайная величина, принимающая свои значения Х_i в некоторой области  на оси OX. Закон распределения задан плотностью вероятностей f(Х) в . Рассмотрим задачу об определении вероятности попадания случайной величины  в интервал  с фиксированными границами a и b, содержащийся в . Если обозначить искомую вероятность P(ab)=Р, то она выражается в виде интеграла:



Этот интеграл можно вычислить по методу статистических испытаний (эксперимент с получением случайных значений Х_i случайной величины ). Если появившееся при данном испытании значение Х_i находится внутри интервала , данное испытание будем считать удачным. После проведения N испытаний подсчитаем число m удачных испытаний и вычислим частоту попадания случайной величины  в интервал :

. (2)

Располагая частотой , мы можем приближённо оценить искомую вероятность p на основании закона больших чисел.

Для этого воспользуемся теоремой Бернулли: если событие А имеет вероятность P и если m – число наступления событий А при N независимых испытаниях, то каково бы ни было постоянное 0

.

При достаточно большом числе испытаний в качестве оценки для интеграла (1) можно взять частоту , т.е.

. (3)

Моделирование эксперимента включает:

1. 
   из совокупности случайных чисел с законом распределения f(Х) извлекается число Х_i;
   
2. 
   случайное число Х_i сравнивается с границами a и b интервала . Результаты сравнения отмечаются специальным признаком , равным единице, если выполнено неравенство
   

a  Х_i  b; (4)

и равным нулю в противном случае;

3. 
   полученная величина  прибавляется к содержимому «счётчика числа удачных испытаний»;
   
4. 
   к содержимому «счётчика количества испытаний» прибавляется единица.
   

После проведения N испытаний определяется приближённое значение искомой вероятности

.

Описанная процедура не требует запоминания всех случайных чисел, извлекаемых в процессе счёта. По ходу вычисления запоминаются только число испытаний N и число удачных испытаний m.

Для того, чтобы метод статистических испытаний можно было считать практически приемлемым, необходимо оценить точность равенства (3) и на этом основании определить число испытаний N для вычисления интеграла (1) с достаточной точностью. Представление о точности можно получить, рассматривая , как случайную величину. Она имеет математическое ожидание



и дисперсию

.

Поэтому средняя квадратичная ошибка равенства (3) будет равна

.

Легко видеть, что максимум достигается при P = 0,5.

Обсудим вопрос о точности метода более подробно. Равенство (3) имеет точность  с надежностью , если для неравенства справедливо соотношение

. (6)

Смысл соотношения (6) можно пояснить на примере. Пусть =0,01; =0,95. Тогда при систематическом употреблении формулы (3) можно утверждать, что в среднем в 95 случаях на 100 испытаний приближенное значение искомой вероятности будет отличаться от её истинного значения p не более как на 0,01.

Свяжем величины  и  с числом испытаний N. Первую ориентировку в этом вопросе можно получить из неравенства Чебышева, справедливого для любой случайной величины. В наших обозначениях оно имеет вид


(54)
. (7)

Сопоставляя это выражение с (6), можно принять

.

Если подставить теперь вместо его значение из (5), получим

.

Отсюда

. (8)

В соответствии с (8) можно вычислить число испытаний N, если заданы ,  и P. Например, если мы хотим, чтобы с надёжностью =0,95 погрешность  не превышала 0,01 при P=0,5, необходимо выполнить не менее N=50 000 испытаний.

Формула (8), полученная на основании неравенства Чебышева, даёт сильно завышенное значение N. Более точную оценку для N можно получить в том случае, если использовать закон распределения случайной величины из равенства (6). Величина имеет (при N) асимптотически нормальное распределение. На этом основании при больших N равенство (6) можно записать в виде:

,

где t_ – величина критического интервала, которая выбирается из таблиц нормального распределения по заданной надёжности . Сравнивая это соотношение с (6) мы видим, что , или

.

Отсюда можно определить значение N:

(9)

Для того, чтобы наглядно представить порядок величины N, обеспечивающей заданную точность, положим, как и прежде, =0,95 и вычислим N для различных значений p и . Результаты расчёта даны в таблице 1.